前言
为什么要引入AVL树?
我们熟知的二叉搜索树虽然在原来二叉树的基础上已经缩短了查找的效率,但是若数据有序,或接近有序的二叉搜索树将会退化成一个单支树,查找的效率相当于在顺序表中搜索元素,有悖引入二叉搜索树的初衷了;这时候就出现了AVL树,可以很好的接近上述问题;怎么解决?请往下看~
接下来本文将用最简洁明了的话语、最详细的代码、最详细的注释,带你深入以及模拟实现一个AVL树;
一、什么是AVL树?
当向二叉搜索树中插入新的结点后,如果能保证每一个结点的左右子树高度差(简称平衡因子)的绝对值不超过1(这里是对树的结点通过左右旋转后),那么他就是一颗AVL树。AVL树降低了树的高度,减少了平均搜索长度,提高了搜索效率;
如果一棵二叉搜索树是高度平衡的,它就是AVL树。如果它有n个结点,其高度可保持在O(log2 n) ,搜索时间复杂度O(log2 n)。
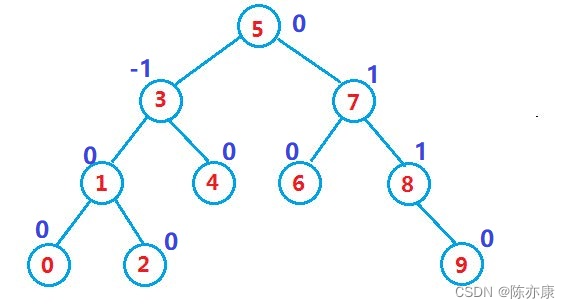
例如下图:(一颗AVL树)
二、模拟实现AVL树
模拟实现AVL树就需要分别实现两个功能,插入和删除,其中,插入最难,因为涉及到左旋右旋调整树的平衡;这里如果能将插入功能实现,那么删除功能的实现就十分容易了;
2.1、定义AVL树
public class AVLTree {
static class TreeNode {
public int val;
public int bf;//平衡因子
TreeNode left;//左子树
TreeNode rigth;//右子树
TreeNode parent;//父亲结点
public TreeNode(int val) {
this.val = val;
}
}
public TreeNode root;//根节点
2.2、插入结点功能
插入结点分两步:
1.先将结点插入到AVL树中(方法和二叉搜索树的插入结点的方式一样);
2.插入以后,根据平衡因子来对树进行调整;
2.2.1、先把值为val的结点插入到AVL树中
思路:
首先看根结点是否为空,若根节点为空说明这棵树还是一个空树,那么就直接创建一个值为val的根节点;
若根节点不为空,就用一个cur指针去遍历这个树的结点,并用一个parent指针记录cur的父亲结点,当cur指向的当前结点值大于val,那么就因该向树的左子树走,若小于val,就因该向树的右边走,直到cur为空时,通过比parent与val值,即可确定插入位置;
代码如下:
public boolean insert(int val) {
TreeNode node = new TreeNode(val);
if(root == null) {
root = node;
return true;
}
TreeNode parent = null;
TreeNode cur = root;
while(cur != null) {
if(cur.val > val) {
//向左寻找
parent = cur;
cur = cur.left;
} else if(cur.val == val) {
//相等就说明插入失败
return false;
} else {
//向右寻找
parent = cur;
cur = cur.right;
}
}
//cur == null
if(parent.val > val) {
parent.left = node;
} else {
parent.right = node;
}
return true;
}2.2.2、根据平衡因子来对树进行调整
平衡因子等于什么?
这里规定为:右树的高度减左树的高度,一旦出现了平衡因子的绝对值大于1,说明这颗树就不平衡了,需要进行旋转使其平衡;
因此首先需要记录平衡因子——新增结点在右树,平衡因子++,新增结点在左树, 平衡因子--;
代码如下:
if(cur == parent.right) {
//新增结点在右树
parent.bf++;
} else {
//新增结点在左树
parent.bf--;
}先来看看为什么要调整?
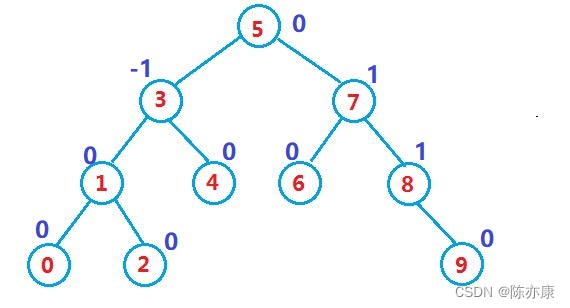
假设树原本是如下样子:
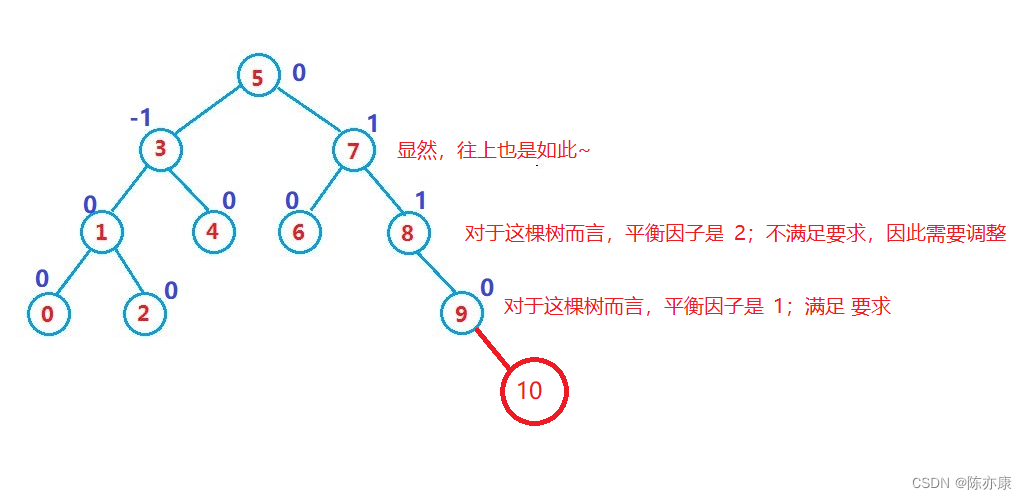
之后,我插入了一个val值为10的结点,那么这颗树就不平衡了(不满足平衡因子了),为什么?看下图:
那么如何旋转呢?接下来先简单了解一下(后面会重点讲)
可以将不平衡的子树进行如下旋转:
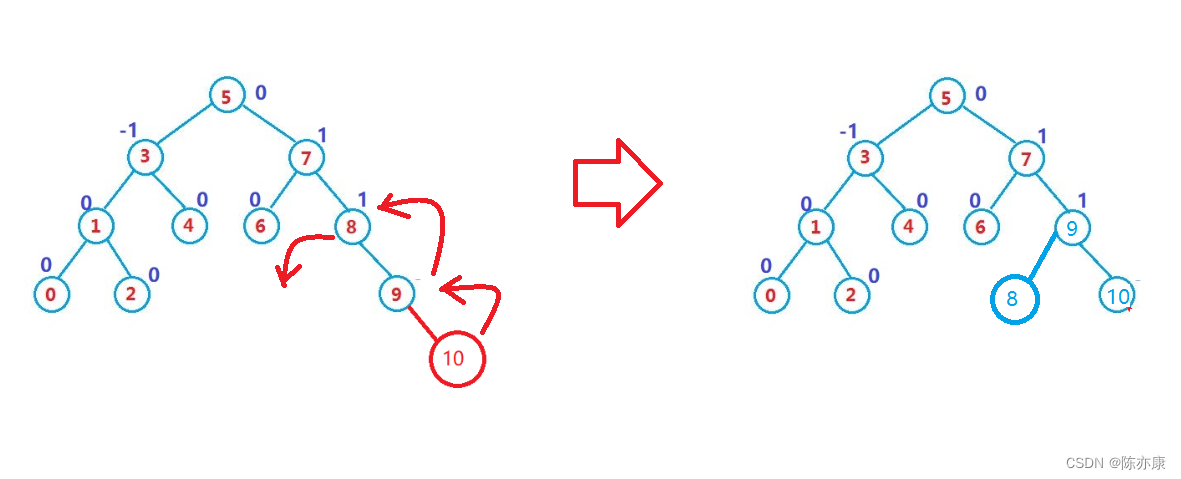
以上只是一种新增结点的方式,但显然,实际情况就右很多种,因此分为以下几种情况:
情况一:平衡因子等于0,这种情况, 树以及平衡;
情况二:平衡因子等于1或-1,这种情况,树不一定平衡,还需要向上去看他的父亲结点是否平衡;
情况三:平衡因子等于2或-2, 这种情况,树一定不平衡,根据实际情况,降低高度;
写成代码就是以下情况:(还没有写如何处理)
if(parent.bf == 0) {
//这里说明以及平衡了,不需要在调整
break;
} else if(parent.bf == 1 || parent.bf == -1) {
//再往上查看结点,有可能不平衡
cur = parent;
parent = cur.parent;
} else {
//一定不平衡
if(parent.bf == 2) {//右树高,需要降低右树的高度
if(cur.bf == 1) {
} else {//cur.bf == -1
}
} else {//parent.bf == -2 左树高,需要降低左树的高度
if(cur.bf == -1) {
} else {//cur.bf == 1
}
}
}针对以上一些不平衡的情况,我们因该如何处理呢?旋转!(重难点!)
2.3、AVL树的旋转
2.3.1、右单旋
什么时候需要右单旋呢?
新结点插入较高左子树的左侧,原因如下图
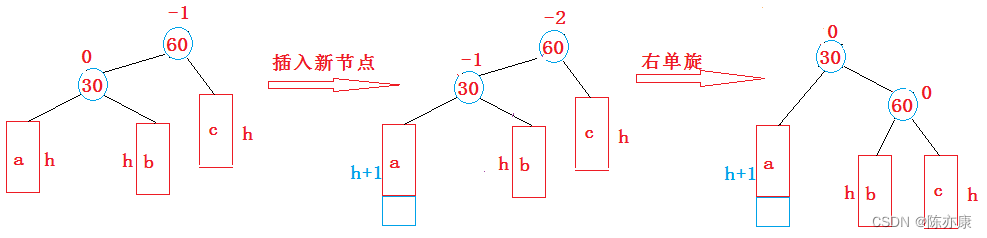
分析:若是插入 较高左子树的左侧 那么代码根据上图的平衡因子的变化,最终代码会来到下图这个位置

那么现在问题就在于,如何进行右单旋,使其变成一颗平衡的树?
如下这棵树:
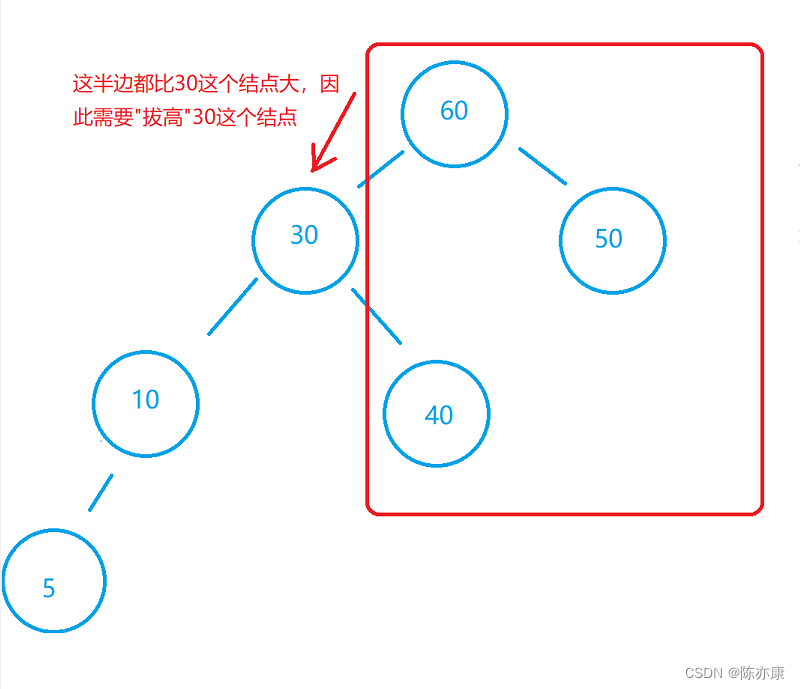
变换后可以得到:
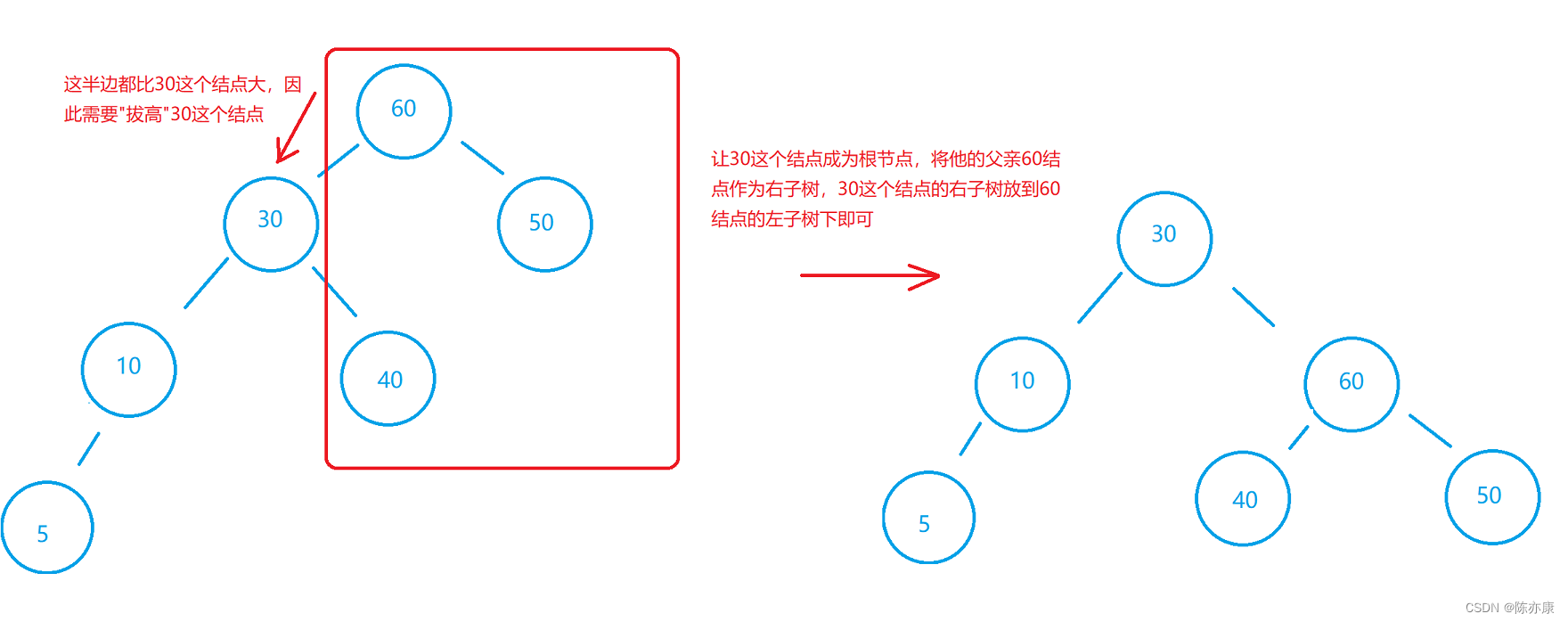
这样左旋转就完了:
parent : 结点60;
subL : 结点30;
subLR:结点40;
代码如下:
private void rotateRight(TreeNode parent) {
TreeNode subL = parent.left;
TreeNode subLR = subL.right;
parent.left = subLR;
subL.right = parent;
subLR.parent = parent;
parent.parent = subL;
}怎么可能这么容易哦~
因为60这个结点不一定是根节点,如下:
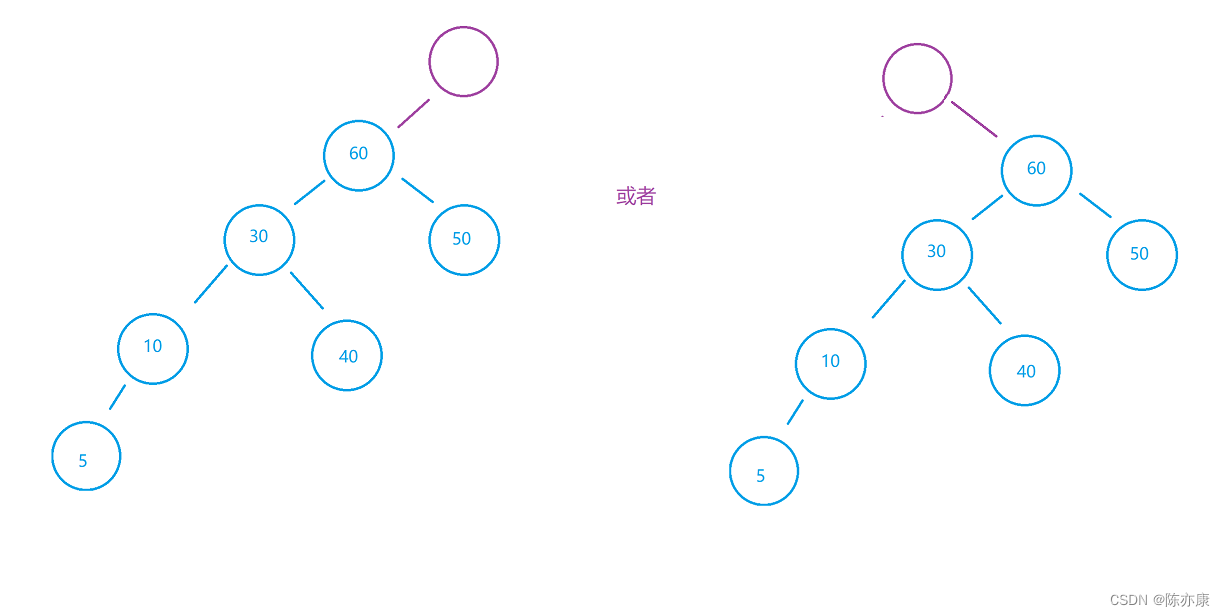
所以,代码还需要分为以下情况:(60有父亲结点和没有父亲结点)
//右单旋
private void rotateRight(TreeNode parent) {
TreeNode subL = parent.left;
TreeNode subLR = subL.right;
parent.left = subLR;
subL.right = parent;
subLR.parent = parent;
//必须先记录parent的父亲
TreeNode pParent = parent.parent;
parent.parent = subL;
//检查parent是否是根节点
if(parent == root) {
root = subL;
root = null;
} else {
//不是根节点,判断parent是左子树还是右子树
if(pParent.left == parent) {
pParent.left = subL;
} else {
pParent.right = subL;
}
subL.parent = pParent;
}
}不光转化完了,还需要调节他的平衡因子,如下:
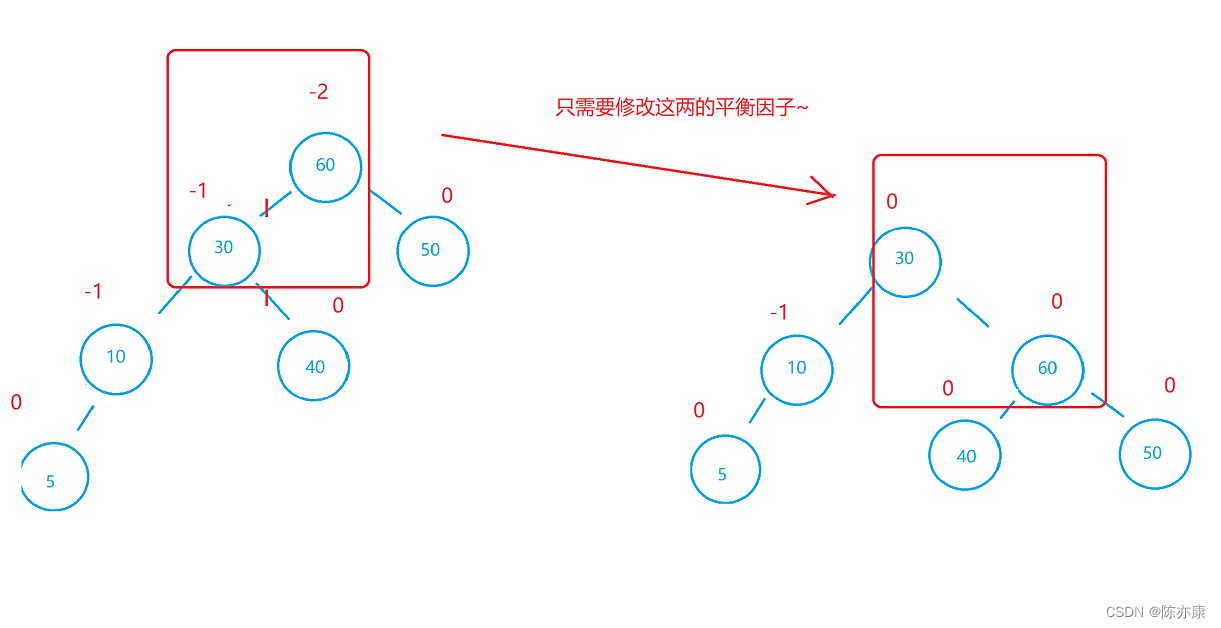
//右单旋
private void rotateRight(TreeNode parent) {
TreeNode subL = parent.left;
TreeNode subLR = subL.right;
parent.left = subLR;
subL.right = parent;
subLR.parent = parent;
//必须先记录parent的父亲
TreeNode pParent = parent.parent;
parent.parent = subL;
//检查parent是否是根节点
if(parent == root) {
root = subL;
root = null;
} else {
//不是根节点,判断parent是左子树还是右子树
if(pParent.left == parent) {
pParent.left = subL;
} else {
pParent.right = subL;
}
subL.parent = pParent;
}
subL.bf = 0;
parent.bf = 0;
}写到这里,以上代码还有一点小问题,就是subLR有可能是空,如下:
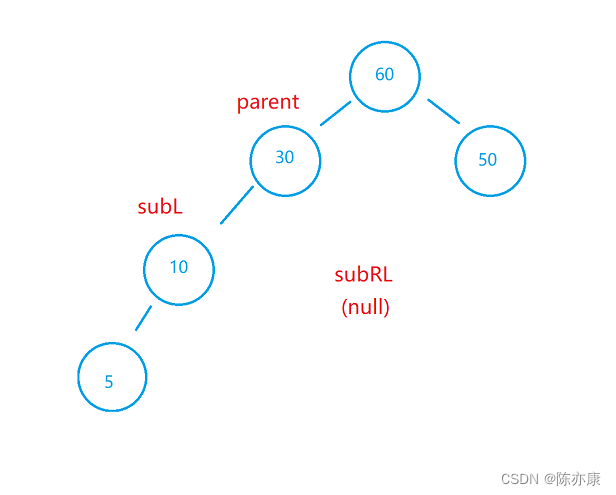
怎么解决呢?实际上如果subRL是null,那么不执行 subRL.parent = parent这行代码即可,那么此时,需要加上一个判断,如下:
//右单旋
private void rotateRight(TreeNode parent) {
TreeNode subL = parent.left;
TreeNode subLR = subL.right;
parent.left = subLR;
subL.right = parent;
if(subLR != null) {
subLR.parent = parent;
}
//必须先记录parent的父亲
TreeNode pParent = parent.parent;
parent.parent = subL;
//检查parent是否是根节点
if(parent == root) {
root = subL;
root = null;
} else {
//不是根节点,判断parent是左子树还是右子树
if(pParent.left == parent) {
pParent.left = subL;
} else {
pParent.right = subL;
}
subL.parent = pParent;
}
subL.bf = 0;
parent.bf = 0;
这样右单旋就完成了~
2.3.2、左单旋
什么时候需要左单旋呢?
新结点插入较高右子树的右侧,原因如下图
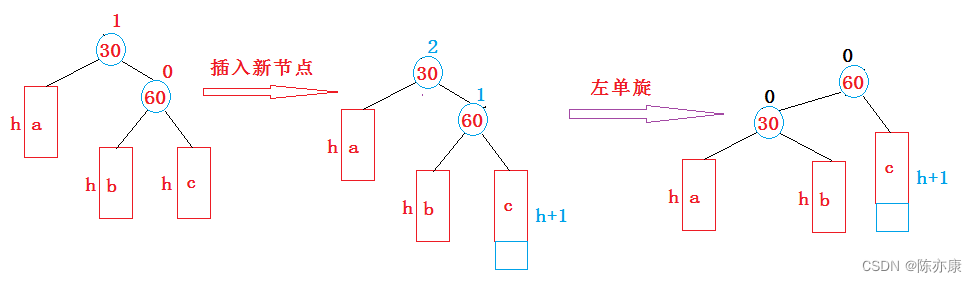
代码上,和右单旋是差不多的,可以参照着右单旋来写:
//左单旋
private void rotateLeft(TreeNode parent) {
TreeNode subR = parent.right;
TreeNode subRL = subR.left;
parent.right = subRL;
subR.left = parent;
if(subRL != null) {
subRL.parent = parent;
}
//必须先记录parent的父亲
TreeNode pParent = parent.parent;
parent.parent = subR;
//检查parent是否为根节点
if(parent == root) {
root = subR;
root.parent = null;
} else {
//不是根节点需要判断parent是左子树还是右子树
if(pParent.left == parent) {
pParent.left = subR;
} else {
pParent.right = subR;
}
subR.parent = pParent;
}
subR.bf = 0;
parent.bf = 0;
}由此通过左单旋,和右单旋也可以看出循环条件为parent != null,原因:一直在搜索不平衡因子是一个向上搜索的过程,直到parent为null,说明已经平衡因子已经调节到了到根节点(修改完了),因此代码就可以修改:
public boolean insert(int val) {
TreeNode node = new TreeNode(val);
if(root == null) {
root = node;
return true;
}
TreeNode parent = null;
TreeNode cur = root;
while(cur != null) {
if(cur.val > val) {
//向左寻找
parent = cur;
cur = cur.left;
} else if(cur.val == val) {
//相等就说明插入失败
return false;
} else {
//向右寻找
parent = cur;
cur = cur.right;
}
}
//cur == null
if(parent.val > val) {
parent.left = node;
} else {
parent.right = node;
}
cur = node;
//调整因子
while(parent != null) {
//新增结点在右树,平衡因子++,新增结点在左树, 平衡因子--
if(cur == parent.right) {
//新增结点在右树
parent.bf++;
} else {
//新增结点在左树
parent.bf--;
}
//检查平衡因子大小
if(parent.bf == 0) {
//这里说明以及平衡了,不需要在调整
break;
} else if(parent.bf == 1 || parent.bf == -1) {
//再往上查看结点,有可能不平衡
cur = parent;
parent = cur.parent;
} else {
//一定不平衡
if(parent.bf == 2) {//右树高,需要降低右树的高度
if(cur.bf == 1) {
//右旋
rotateLeft(parent);
} else {//cur.bf == -1
}
} else {//parent.bf == -2 左树高,需要降低左树的高度
if(cur.bf == -1) {
//右旋
rotateRight(parent);
} else {//cur.bf == 1
}
}
}
}
}这样左单旋就完成了~
2.3.3、左右双旋
什么时候需要右单旋呢?
新结点插入较高左子树的右侧(先左单旋再右单旋),原因如下图:
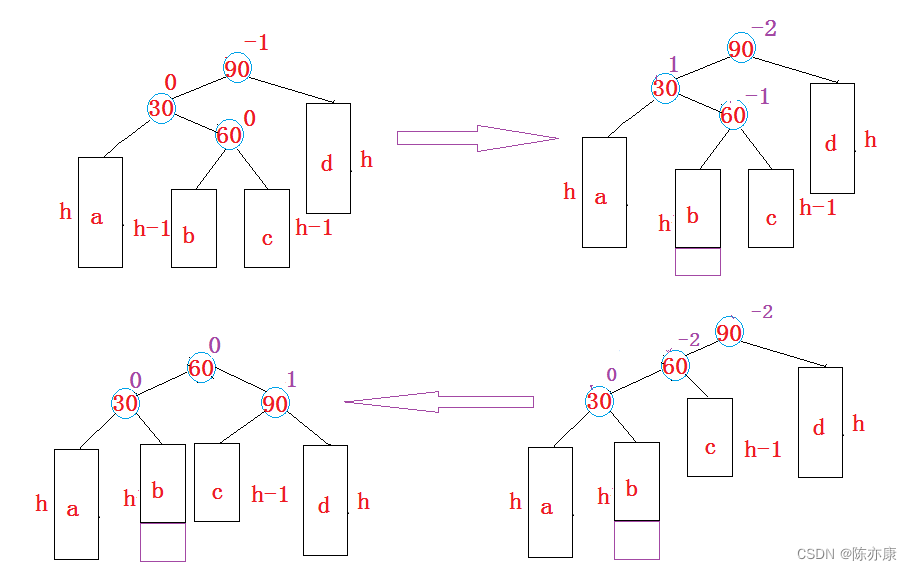
像这样的一棵树如果只是进行简单的左旋或右旋,相当于旋转了个寂寞,如下:
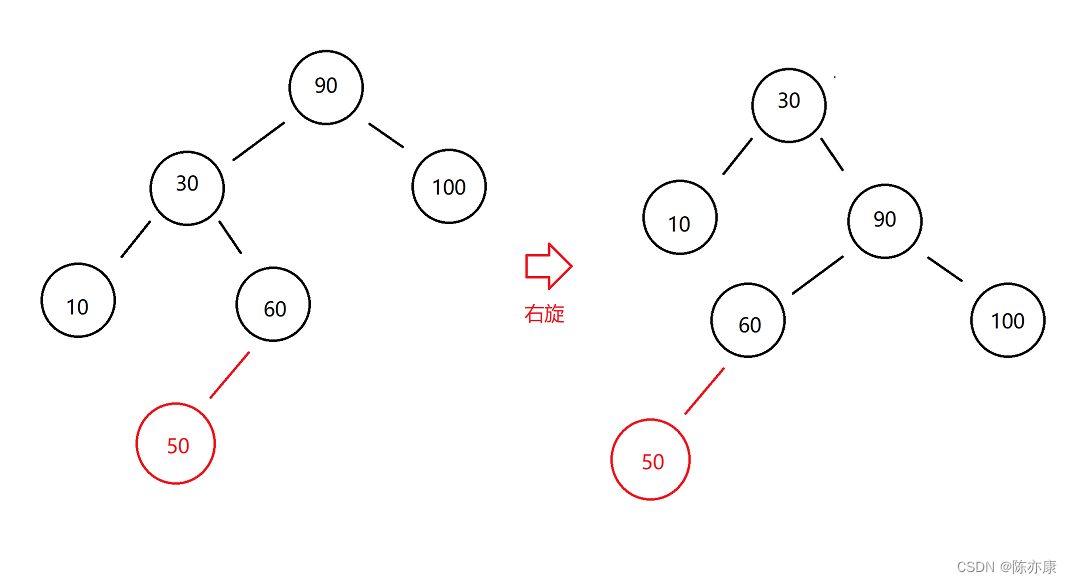
那怎么办呢?不妨这样做~
第一步:可以先对30这颗子树进行左旋,如下:
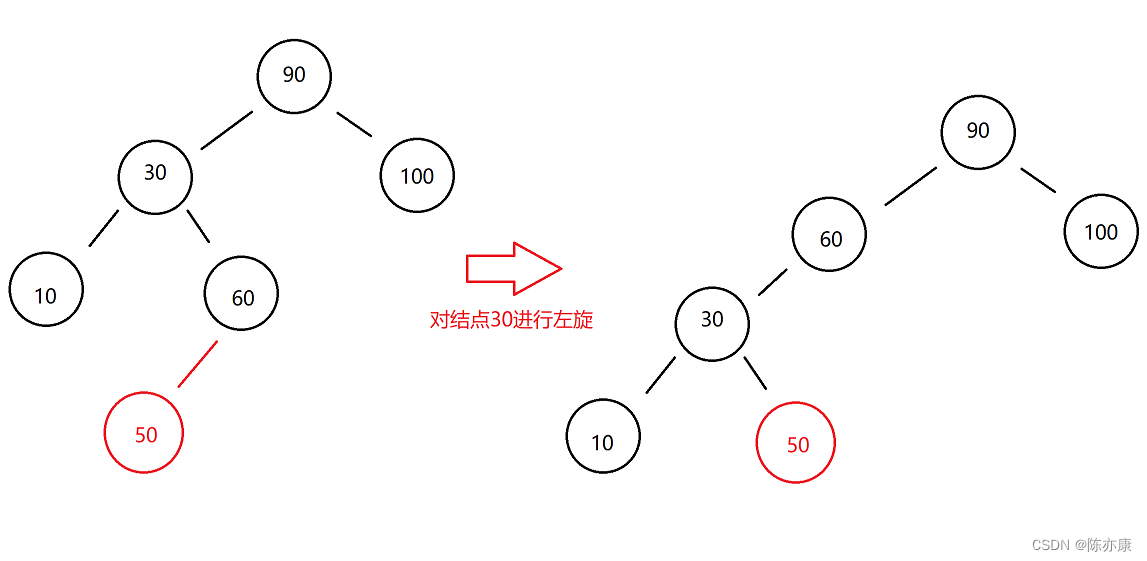
第二步:再将90这个parent结点进行右旋,如下:
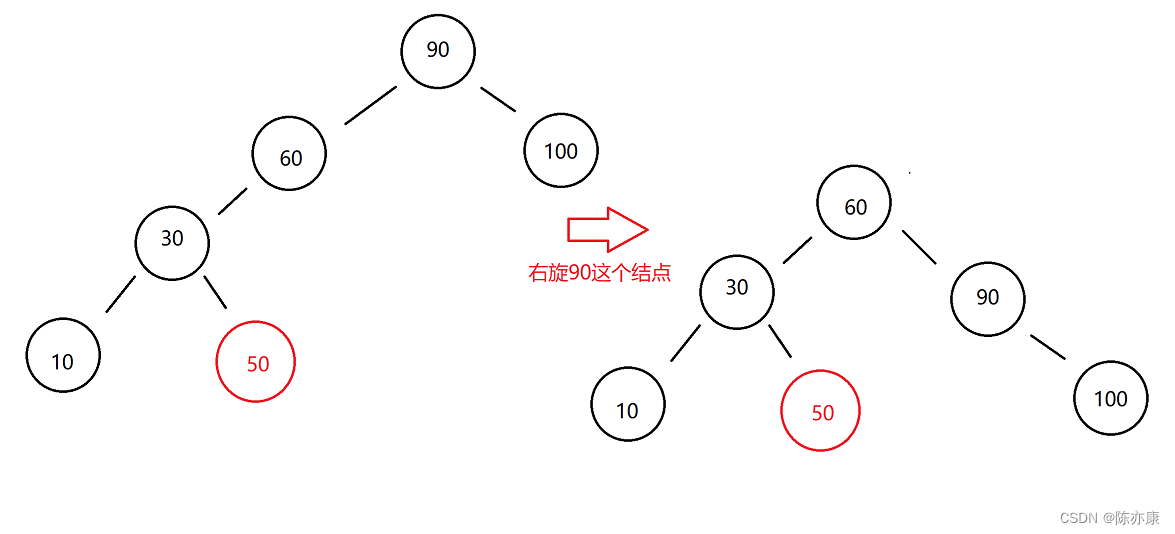
那么此时,他就是一个高度平衡的AVL树了~
左右双旋,实际上就是左单旋 + 右单旋,并且这部分代码之前就写好了,所以直接拿来用就可以,值得注意的一点是,要旋转的结点,这个可以自己画画图就明白了;
代码如下:
//左右双旋
private void rortateLR(TreeNode parent) {
//选左旋后右旋
rotateLeft(parent.left);//注意旋转的是parent的左子树
rotateRight(parent);
}这样就完了吗?
当然没有~这里还有平衡因子没有修改呢!
这里平衡因子分两种情况,接下来,我将用一张图告诉你该如何解决!如下:
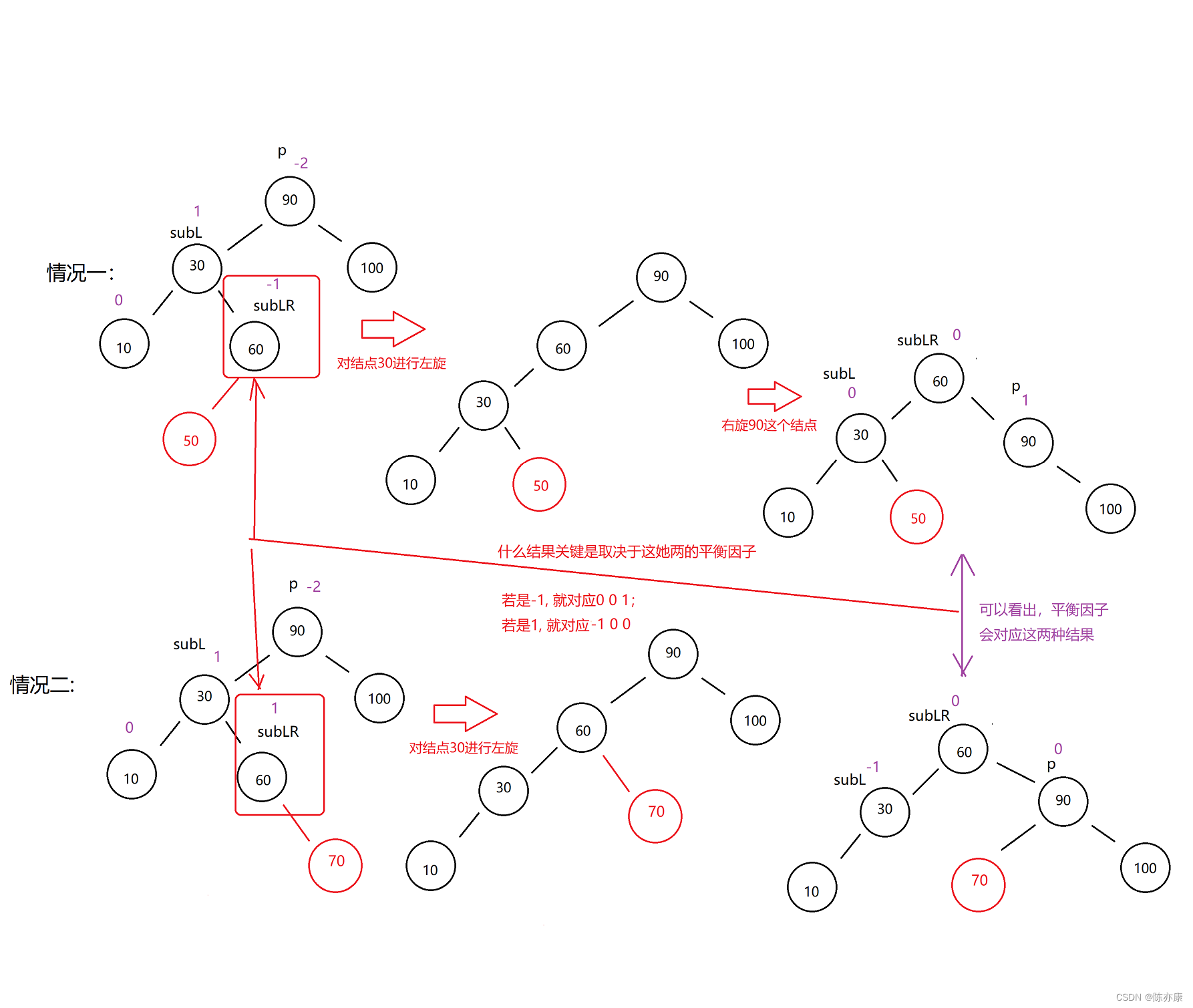
因此,代码如下:
//左右双旋
private void rortateLR(TreeNode parent) {
TreeNode subL = parent.left;
TreeNode subLR = subL.right;
int bf = subLR.bf;
//选左旋后右旋
rotateLeft(parent.left);//注意旋转的是parent的左子树
rotateRight(parent);
if(bf == -1) {
subL.bf = 0;
subLR.bf = 0;
parent.bf = 1;
} else if(bf == 1){
subL.bf = -1;
subLR.bf = 0;
parent.bf= 0;
} //bf == 0,这里本身就是平衡的,就不用修改
}这样左右双旋就完成辽~
2.3.4、右左双旋
什么时候需要右左双旋呢?
新结点插入较高右子树的左侧,原因如下图
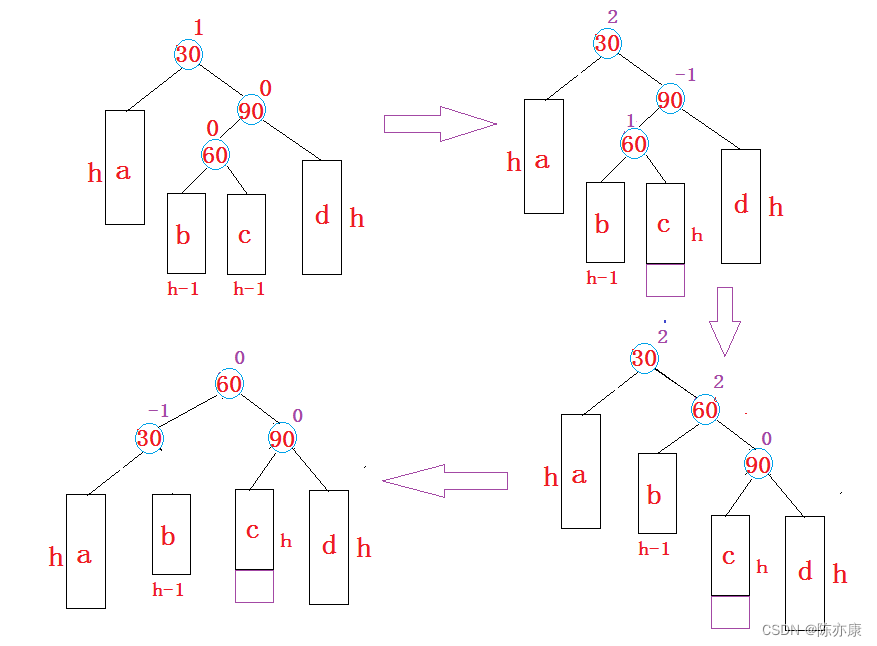
这里代码和左右双旋差不多,分析思路也一样,所以这里就不展开啦,代码如下:
//右左双旋
private void rottateRL(TreeNode parent) {
TreeNode subR = parent.right;
TreeNode subRL = subR.left;
int bf = subRL.bf;
rotateRight(parent.right);
rotateLeft(parent);
if(bf == 1) {
parent.bf = -1;
subR.bf = 0;
subRL.bf = 0;
} else if(bf == -1) {
subRL.bf = 0;
parent.bf = 0;
subR.bf = 1;
}
}由以上的各种旋转,那么之前遗留的insert函数中的代码也就完整啦,如下:
public boolean insert(int val) {
TreeNode node = new TreeNode(val);
if(root == null) {
root = node;
return true;
}
TreeNode parent = null;
TreeNode cur = root;
while(cur != null) {
if(cur.val > val) {
//向左寻找
parent = cur;
cur = cur.left;
} else if(cur.val == val) {
//相等就说明插入失败
return false;
} else {
//向右寻找
parent = cur;
cur = cur.right;
}
}
//cur == null
if(parent.val > val) {
parent.left = node;
} else {
parent.right = node;
}
node.parent = parent;/
cur = node;
//调整因子
while(parent != null) {
//新增结点在右树,平衡因子++,新增结点在左树, 平衡因子--
if(cur == parent.right) {
//新增结点在右树
parent.bf++;
} else {
//新增结点在左树
parent.bf--;
}
//检查平衡因子大小
if(parent.bf == 0) {
//这里说明以及平衡了,不需要在调整
break;
} else if(parent.bf == 1 || parent.bf == -1) {
//再往上查看结点,有可能不平衡
cur = parent;
parent = cur.parent;
} else {
//一定不平衡
if(parent.bf == 2) {//右树高,需要降低右树的高度
if(cur.bf == 1) {
//左旋
rotateLeft(parent);
} else {//cur.bf == -1
//右左双旋
rottateRL(parent);
}
} else {//parent.bf == -2 左树高,需要降低左树的高度
if(cur.bf == -1) {
//右旋
rotateRight(parent);
} else {//cur.bf == 1
//左右双旋
rortateLR(parent);
}
}
//走完以上代码即哦平衡
break;
}
}
return true;
}
2.3、验证AVL树
验证一棵树是否为AVL树只需要验证他的以下两个性质即可~
1)、验证其为二叉搜索树
- 如果中序遍历可得到一个有序的序列,就说明为二叉搜索树;
2)、验证其为平衡树
- 每个节点子树高度差的绝对值不超过1(注意节点中如果没有平衡因子)
- 节点的平衡因子是否计算正确
代码如下:
//验证平衡
public boolean isBalanced(TreeNode root) {
if(root == null) {
return true;
}
int leftH = heigh(root.left);
int rightH = heigh(root.right);
if(rightH - leftH != root.bf) {
System.out.println("结点:" + root.val + "的平衡因子异常");
return false;
}
return Math.abs(leftH - rightH) <= 1 &&
isBalanced(root.left) &&
isBalanced(root.right);
}
//求树的高度
private int heigh(TreeNode root) {
if(root == null) {
return 0;
}
int leftH = heigh(root.left);
int rightH = heigh(root.right);
return leftH > rightH ? leftH + 1 : rightH + 1;
}
//验证顺序
public void dfs(TreeNode root) {
if(root == null) {
return;
}
dfs(root.left);
System.out.print("root = " + root.val + "; ");
dfs(root.right);
2.4、删除结点
删除结点这里不需要掌握,感兴趣的可以自己实现一下;
如果要删除结点,实际上和二叉搜索树结点的删除思路相似,只不过需要进行对平衡因子的更新,并且若出现了不平衡需要进行左旋或者右旋;
代码如下:
/**
* 删除操作
*/
public AVLNode<T> deleteNode(AVLNode T,T value){
if(T==null){
return null;
}else{
//往左走
if((Integer)value<(Integer) T.data){
T.lchild = deleteNode(T.lchild,value); //函数返回新的根节点(所以要重新建立孩子与双亲间的联系)
if(getHeight(T.rchild)-getHeight(T.lchild)>=2){ //删掉左子树的孩子结点,肯定是右边可能会高过左边的情况
if(getHeight(T.rchild.lchild)>getHeight(T.rchild.rchild)){ //左子树的 右子树比左子树的左子树要高
//RL旋转
T = doubleRotateWithRight(T); //记住,因为旋转后,根节点会发生变化,一定要重新接收根结点
}else{
//RR
T = singleRotateWithLeft(T);
}
}
//往右走
}else if((Integer)value>(Integer)T.data){
T.rchild = deleteNode(T.rchild,value);
if(getHeight(T.lchild)-getHeight(T.rchild)>=2){ //删掉右子树的孩子结点,肯定是左边可能会高过右边的情况
if(getHeight(T.lchild.rchild)>getHeight(T.lchild.lchild)){
//LR旋转
T = doubleRotateWithLeft(T);
}else{
//LL
T = singleRotateWithRight(T);
}
}
}else{
//找到了要删除的结点
//1. 没有左右孩子,删除的是叶子节点 (不用判断是否需要修复--旋转)
if(T.lchild==null&&T.rchild==null){
T = null;
//2. 删除的结点只有左孩子或右孩子
}else {
if(T.lchild!=null){
T = T.lchild;
}else if(T.rchild!=null){
T = T.rchild;
}else{
//3. 删除的结点左右孩子都有
T.data = find_min_value(T.rchild); //找到最小节点,替换
T.rchild = deleteNode(T.rchild,(T)T.data); //删除替换的最小的那个结点
//判断旋转
if(getHeight(T.lchild)-getHeight(T.rchild)>=2){
if(getHeight(T.lchild.rchild)-getHeight(T.lchild.lchild)>=2){
//LR
T = doubleRotateWithLeft(T);
}else{
//LL
T = singleRotateWithRight(T);
}
}
}
}
}
}
if(T!=null){
//重新计算高度
T.height = Max(getHeight(T.lchild),getHeight(T.rchild))+1;
}
//返回新的根节点
return T;
}
/**
* 找到最小的结点值
*/
public T find_min_value(AVLNode T){
if(T.lchild==null){
return (T) T.data;
}else{
return find_min_value(T.lchild);
}
}
/**
* 用于比较两棵子树高度,比较哪边高 ,用于节点高度 = Max(T.lchild.height,T.rchild.height)+1
*/
public int Max(int lHeight,int rHeight){
if(lHeight>=rHeight){
return lHeight;
}else{
return rHeight;
}
}
/**
* 获取结点高度,因为可能计算高度的时候,左右孩子结点很可能为空,如果不用这个方法判断的话,会导致nullPointerException
*/
public int getHeight(AVLNode T){
if(T==null){
return -1;
}else{
return T.height;
}
}
三、性能分析
AVL树是一棵绝对平衡的二叉搜索树,其要求每个节点的左右子树高度差的绝对值都不超过1,这样可以保证查询时高效的时间复杂度,即 log2(N);
AVL树不适合大量的插入和删除,因为要不断维持本身AVL树平衡的性质,但是他的适合查找数据,速度相当快;也就是说他的平衡说通过大量旋转换来的~
总结:
如果需要 一种查询高效且有序的数据结构,而且数据的个数为静态的(即不会改变),可以考虑AVL树,但一个结构经常修 改,就不太适合。

