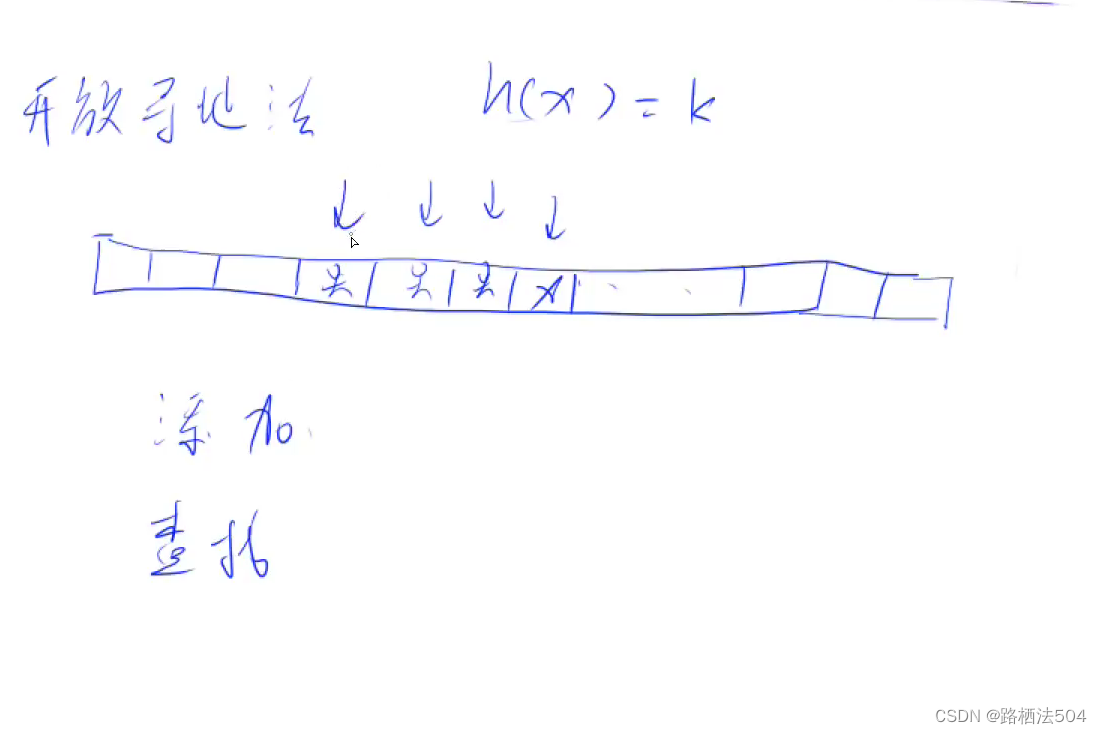
//开放寻址法
//数组长度一般要开到题目数据范围的2~3倍
#include<iostream>
#include<cstring>
using namespace std;
//null代表无穷大
//最大和最小
//0x3f3f3f3f = 1061109567，0xc0c0c0c0 = -1061109568
//0x3f3f3f3f的值比int的最大值要小，但是它仍然可以被当做int的无穷大
//这是因为在很多算法中，我们需要一个比较大的数来表示无穷大
//但是又不能超过int类型的范围。0x3f3f3f3f是一个比较好的选择
//因为它既不会溢出，又比int的最大值小很多
//同时也满足“无穷大加无穷大还是无穷大”的需求
//因此，0x3f3f3f3f通常被用来表示int类型的无穷大
const int N = 2e5 + 3, null = 0x3f3f3f3f;//取质数的方法和之前一样
int h[N], n, x;
string op;

int find(int x)
{
	int k = (x % N + N) % N;
	//不会死循环因为数组开的够大
	while (h[k] != null && h[k] != x)//满足条件就向后找
	{
		k++;
		if (k == N) k = 0;//如果从k后都找不到，就从前遍历
	}
	return k;//若没有元素抢占位置则k为插入位置，若有则为返回查询的位置
}

int main()
{
	ios::sync_with_stdio(0), cin.tie(0), cout.tie(0);
	cin >> n;
	memset(h, 0x3f, sizeof h);
	while (n--)
	{
		cin >> op >> x;
		int k = find(x);
		if (op == "I") h[k] = x;
		else
		{
			if (h[k] != null) cout << "Yes" << '\n';
			else cout << "No" << '\n';
		}
	}
	return 0;
}