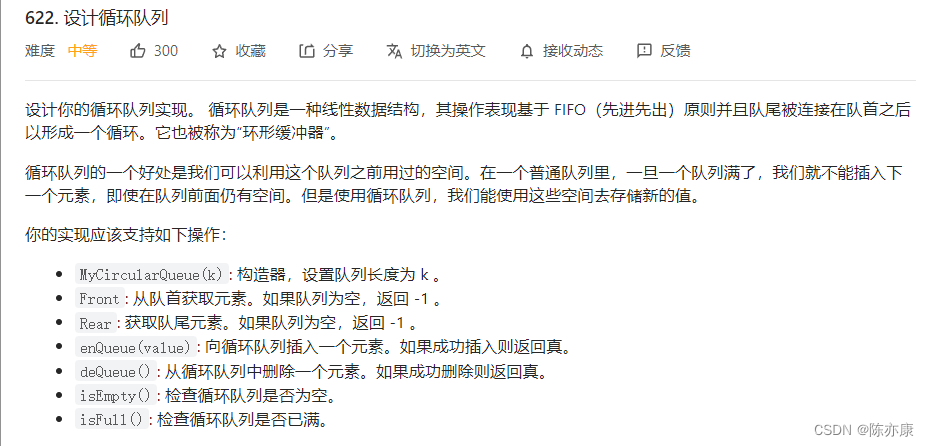
分析：

     两种解题思路，一种是计数法，还有一种是浪费空间法，为什么这么说呢，看下图：

 

 

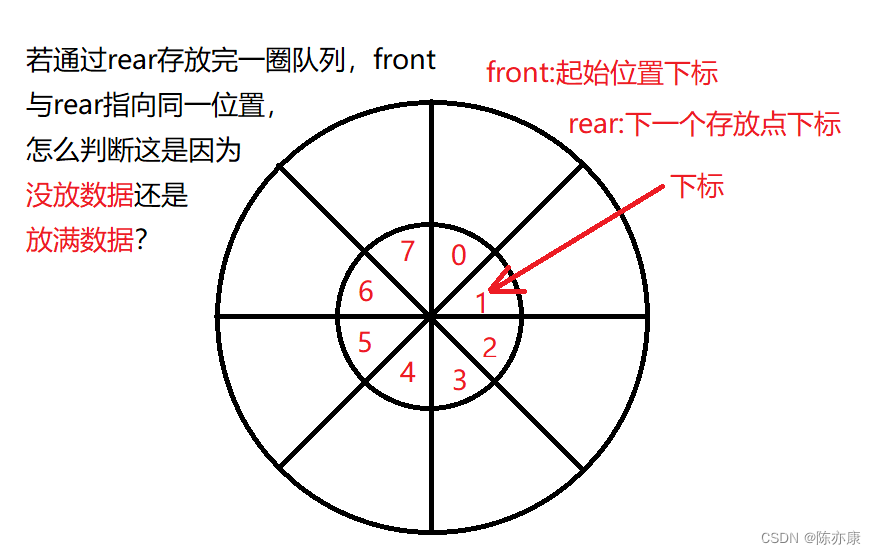
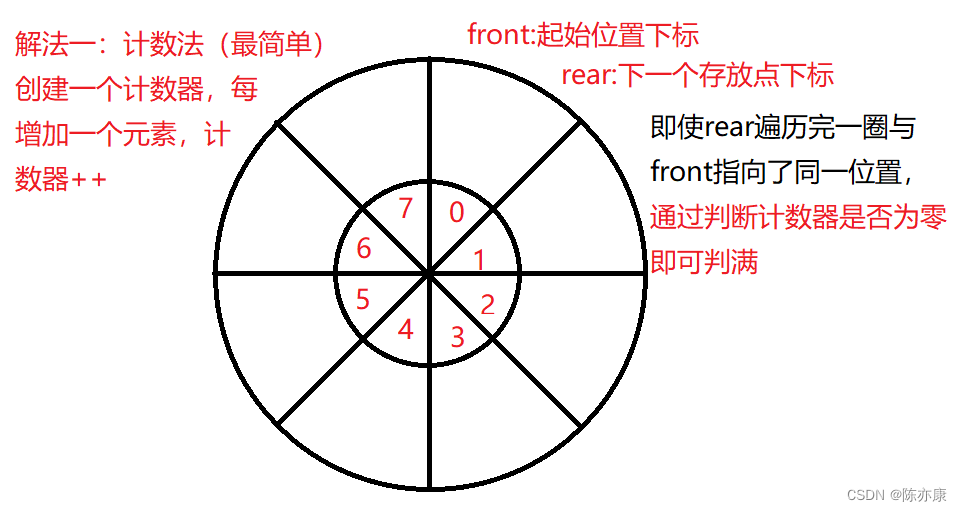
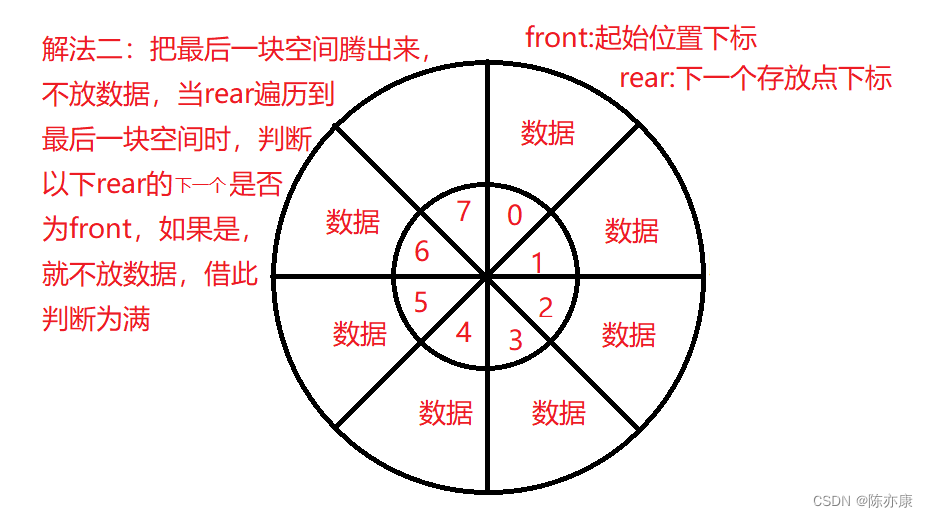
 解法一：

class MyCircularQueue {
    public int[] array;
    private int front;
    private int rear;
    private int usedSize;
    public MyCircularQueue(int k) {
        array = new int[k];
    }
    //插入数据
    public boolean enQueue(int value) {
        if(isFull()){
            return false;
        }
        else{
            array[rear] = value;
            //不可以单纯的rear++;会溢出，就不是循环了
            rear = (rear + 1) % array.length;
            usedSize++;
            return true;
        }
    }
    //删除元素
    public boolean deQueue() {
        if(isEmpty()){
            return false;
        }
        front = (front + 1) % array.length;
        usedSize--;
        return true;
    }
    //获取首元素
    public int Front() {
        if(isEmpty()){
            return -1;
        }
        return array[front];
    }
    //获取尾元素
    public int Rear() {
        if(isEmpty()){
            return -1;
        }
        return rear == 0 ? array[array.length - 1] : array[rear - 1];
    }
    //检查是否为空
    public boolean isEmpty() {
        if(usedSize == 0){
            return true;
        }
        return false;
    }
    //是否为满
    public boolean isFull() {
        return usedSize == array.length;
    }
}

解法二：

class MyCircularQueue {
    public int[] array;
    private int front;
    private int rear;
    public MyCircularQueue(int k) {
        array = new int[k + 1];
    }
    //插入数据
    public boolean enQueue(int value) {
        if(isFull()){
            return false;
        }
        else{
            array[rear] = value;
            //不可以单纯的rear++;会溢出，就不是循环了
            rear = (rear + 1) % array.length;
            return true;
        }
    }
    //删除元素
    public boolean deQueue() {
        if(isEmpty()){
            return false;
        }
        front = (front + 1) % array.length;
        return true;
    }
    //获取首元素
    public int Front() {
        if(isEmpty()){
            return -1;
        }
        return array[front];
    }
    //获取尾元素
    public int Rear() {
        if(isEmpty()){
            return -1;
        }
        return rear == 0 ? array[array.length - 1] : array[rear - 1];
    }
    //检查是否为空
    public boolean isEmpty() {
        if(rear == front){
            return true;
        }
        return false;
    }
    //是否为满
    public boolean isFull() {
        return (rear + 1) % array.length == front;
    }
}