双端队列

定义

概念

双端队列是普通队列的扩展，是指允许两端都可以进行入队和出队操作的队列（即可以在队头进行入队和出队操作，也可以在队尾进行入队和出队操作的队列）。其元素的逻辑结构仍然是线性结构，可以采用顺序存储，也可以采用链式存储。将队列的两端分别称为前端和后端，两端都可以入队和出队。

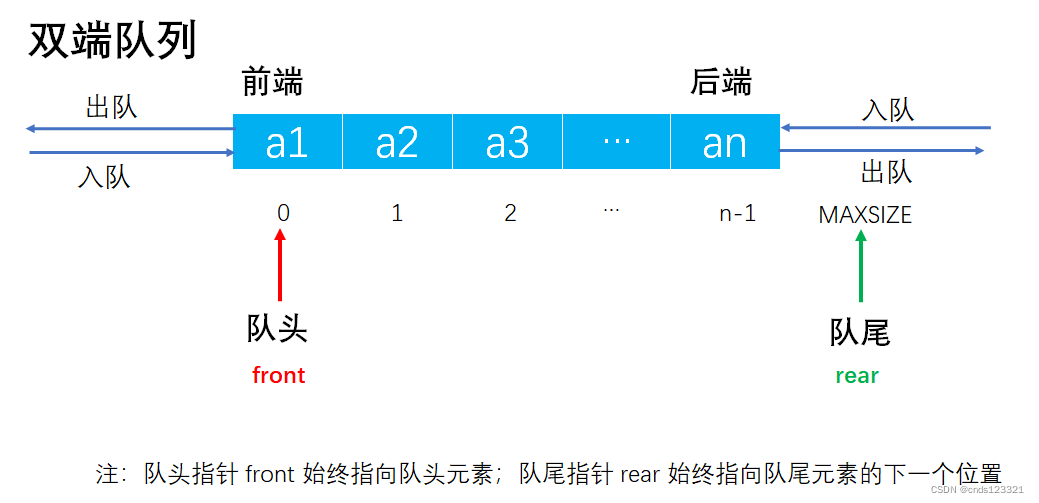
在双端队列入队时，前端进的元素排列在队列中后端进的元素的前面，后端进的元素排列在队列中前端进的元素的后面。在双端队列出队时，无论是前端还是后端出队，先出的元素排列在后出的元素的前面。

除了上面的双端队列之外，还有两类受限的双端队列：

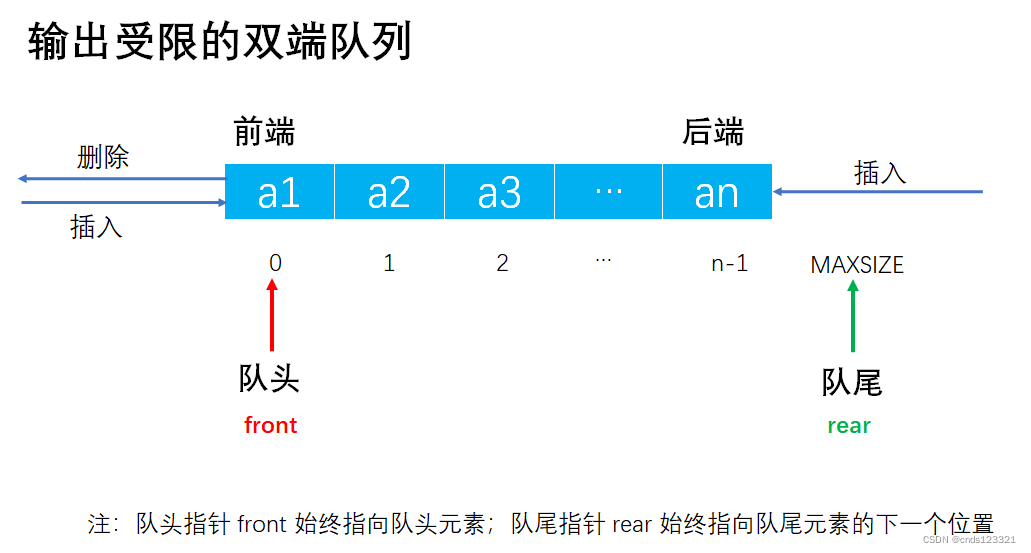
• 输出受限的双端队列：允许在一端进行插入和删除，但在另一端只允许插入的双端队列称为输出受限的双端队列。

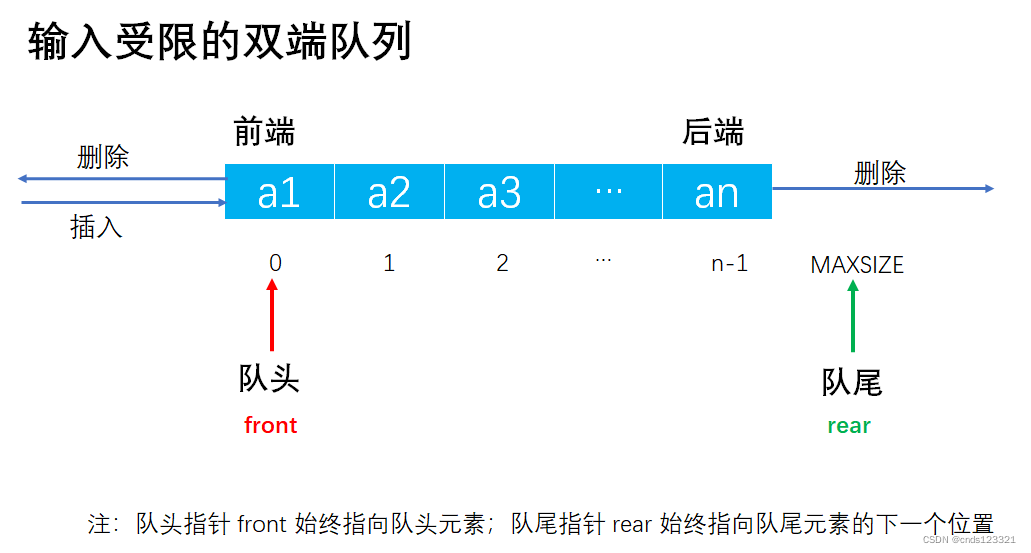
• 输入受限的双端队列：允许在一端进行插入和删除，但在另一端只允许删除的双端队列称为输入受限的双端队列。若限定双端队列从某个端点插入的元素只能从该端点删除，则该双端队列就变成了两个栈底相邻接的栈。

双端队列既可以采用顺序存储，也可以采用链式存储实现。下面所讲的是顺序存储实现，但也提供了链式存储实现代码。

结构体

/**
 * 双端队列结构体定义，跟循环队列的一样，只是 rear 在双端队列中名为 back
 */
typedef struct {
    /**
     * 数据域，存储循环队列中的数据
     */
    int data[MAXSIZE];
    /**
     * 指针域，存储循环队列中队头元素的位置
     */
    int front;
    /**
     * 指针域，存储循环队列中队尾元素的位置
     */
    int back;
} DoubleEndedQueue;

特点

• 输入受限的双端队列是指只能从队列一端输入，可以从两端输出的队列。
• 输出受限的双端队列是指只能从队列一端输出，可以从两端输出的队列。
• 如果双端队列允许从一端输入，从另一端输出，就是普通的队列；如果双端队列只允许从一端输入和输出，就是普通的栈。因此双端队列同时具有队列和栈两种数据结构的性质。

基本操作

注，完整代码请参考：

• DoubleEndedQueue.c
• DoubleEndedQueue.java
• DoubleEndedQueueTest.java
• LinkedDoubleEndedQueue.c)
• LinkedDoubleEndedQueue.java
• LinkedDoubleEndedQueueTest.java

一些注意事项：

• DoubleEndedQueue 表示顺序存储的双端队列；LinkedDoubleEnedQueue 表示链式存储的双端队列。
• 其中顺序存储的双端队列中底层是使用的循环队列，为了能够充分分配的空间。
• 双端队列的结构体中的指针域虽然名字是 front 和 back，但是仍然表示队头指针和队尾指针，而队头指针也仍然指向队头元素，队尾指针指向队尾元素的下一位置。
• DoubleEnedQueue 实现的双端队列大部分代码与循环队列的一致，关于循环队列请参考：文档-循环队列。
• 关于有些图中是 queue 和 deque 这个不重要，是画图时忘了修改，它们都表示队列，勿要关注。

概述

双端队列的常见操作如下：

• void init(DoubleEndedQueue *deque)：初始化双端队列。其中 deque 表示双端队列。
• int isEmpty(DoubleEndedQueue deque)：判断双端队列是否为空。其中 deque 表示双端队列。如果双端队列为空则返回 1，否则返回 0 表示非空。
• int isFull(DoubleEndedQueue deque)：判断双端队列是否已满。其中 deque 表示双端队列。如果双端队列已满则返回 1，否则返回 0。
• int pushFront(DoubleEndedQueue *deque, int ele)：从队头将元素入队。其中 deque 表示双端队列；ele 表示待入队的元素。如果队已满则不能入队，返回 0 表示入队失败；否则如果入队成功则返回 1。
• int pushBack(DoubleEndedQueue *deque, int ele)：从队尾将元素入队。其中 deque 表示双端队列；ele 表示待入队的元素。如果队已满则不能入队，返回 0 表示入队失败；否则如果入队成功则返回 1。
• int popFront(DoubleEndedQueue *deque, int *ele)：从队头将元素出队。其中 deque 表示双端队列；ele 用来保存出队元素。如果队空则不能出队，返回 0 表示出队失败；否则如果出队成功则返回 1。
• int popBack(DoubleEndedQueue *deque, int *ele)：从队尾将元素出队。其中 deque 表示双端队列；ele 用来保存出队元素。如果队空则不能出队，返回 0 表示出队失败；否则如果出队成功则返回 1。
• int size(DoubleEndedQueue deque)：获取双端队列中的元素个数。其中 deque 表示双端队列。返回双端队列中的元素个数。
• int getFront(DoubleEndedQueue deque, int *ele)：获取双端队列中的队头元素。其中 deque 表示双端队列；ele 用来保存队头元素。如果队空则不能获取到队头元素，返回 0 表示获取失败；如果获取成功则返回 1。
• int getBack(DoubleEndedQueue deque, int *ele)：获取双端队列中的队尾元素。其中 deque 表示双端队列；ele 用来保存队尾元素。如果队空则不能获取到队尾元素，返回 0 表示获取失败；如果获取成功则返回 1。
• void clear(DoubleEndedQueue *deque)：清空双端队列。其中 deque 表示双端队列。
• void print(DoubleEndedQueue deque)：打印双端队列所有元素。其中 deque 表示双端队列。

init

初始化双端队列。

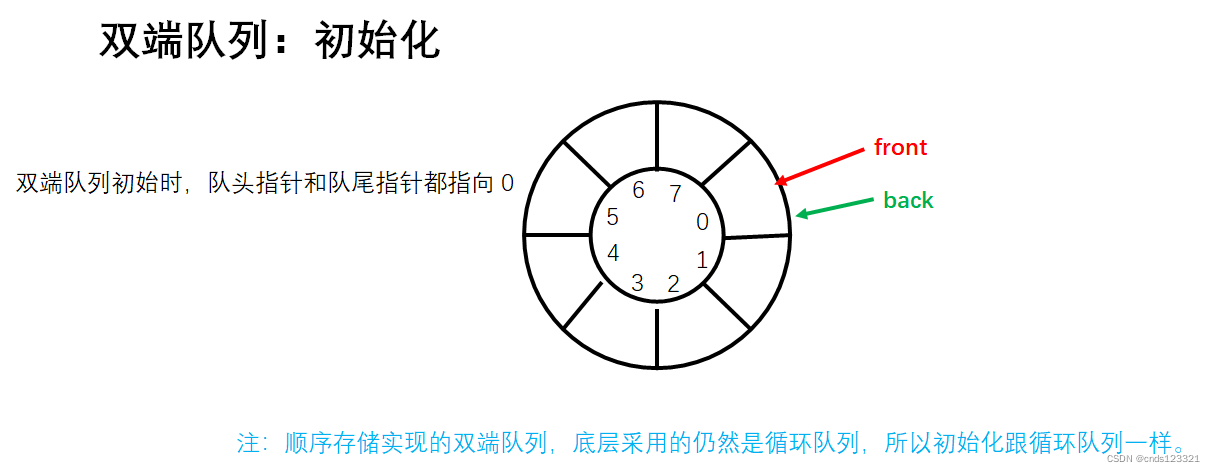
实现步骤：

• 将队头指针 front 和队尾指针 back 都指向 0，表示空队列。

实现代码如下：

/**
 * 初始化双端队列
 * @param deque 待初始化的双端队列
 */
void init(DoubleEndedQueue *deque) {
    // 双端队列初始时，队头指针和队尾指针仍然都指向 0，表示是空队列
    deque->front = 0;
    deque->back = 0;
}

isEmpty

判断双端队列是否为空。如果为空则返回 1，否则返回 0 表示非空。

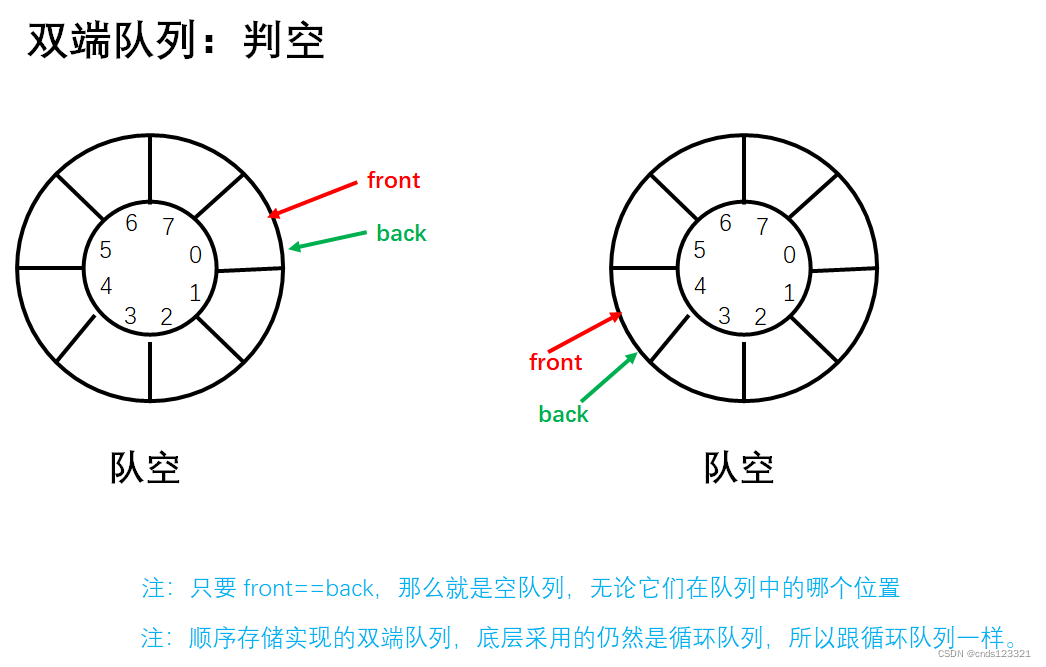
实现步骤：

• 判断队头指针 front 和队尾指针 back 是否指向同一位置，即 deque.front==deque.back。

实现代码如下：

/**
 * 判断双端队列释放为空
 * @param deque 双端队列
 * @return 如果双端队列为空则返回 1，否则返回 0 表示非空
 */
int isEmpty(DoubleEndedQueue deque) {
    // 只要队头指针和队尾指针相等，那么表示双端队列为空，无论指针在哪个位置
    if (deque.front == deque.back) {
        return 1;
    } else {
        return 0;
    }
}

isFull

判断双端队列是否已经满队。如果已满则返回 1，否则返回 0 表示未满。

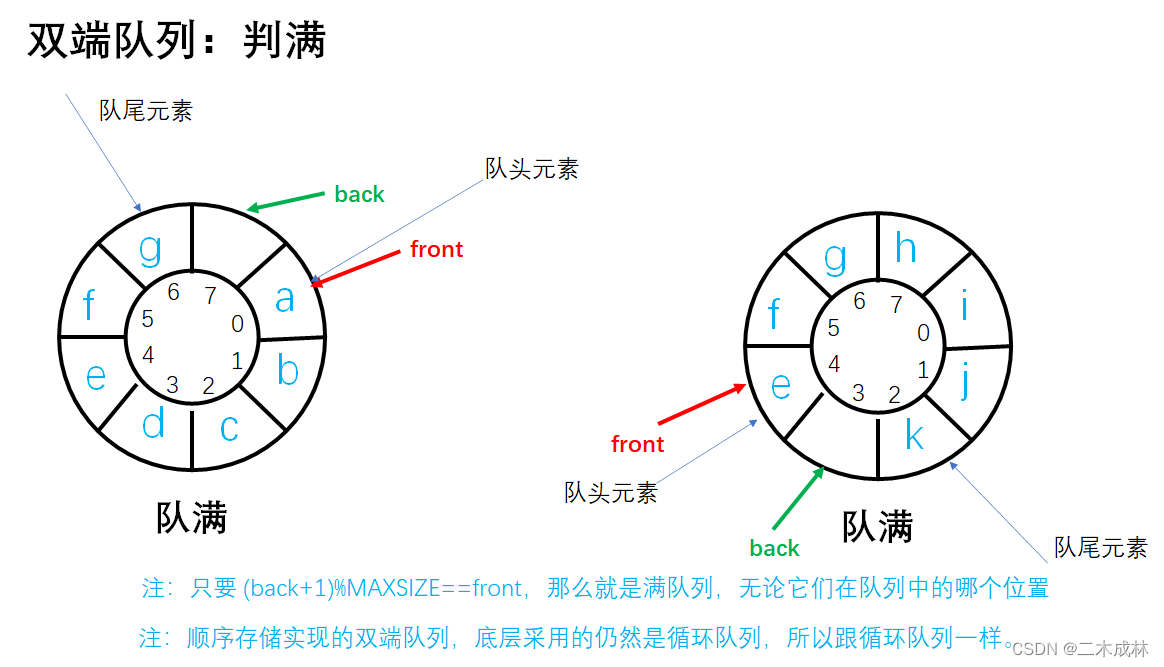
实现步骤：

• 如果满足条件 (queue.back+1)%MAXSIZE==queue.front，那么就认为队满。

实现代码如下：

/**
 * 判断双端队列是否已满
 * @param queue 双端队列
 * @return 如果双端队列已满则返回 1，否则返回 0 表示队列非满
 */
int isFull(DoubleEndedQueue deque) {
    // 判断条件跟循环队列一样，因为底层就是循环队列
    if ((deque.back + 1) % MAXSIZE == deque.front) {
        return 1;
    } else {
        return 0;
    }
}

pushFront

将元素从队头入队。如果队未满才能入队，否则返回 0 表示入队失败。如果入队成功则返回 1。以 deque=[a, b, c]; ele=x 为例如图所示：

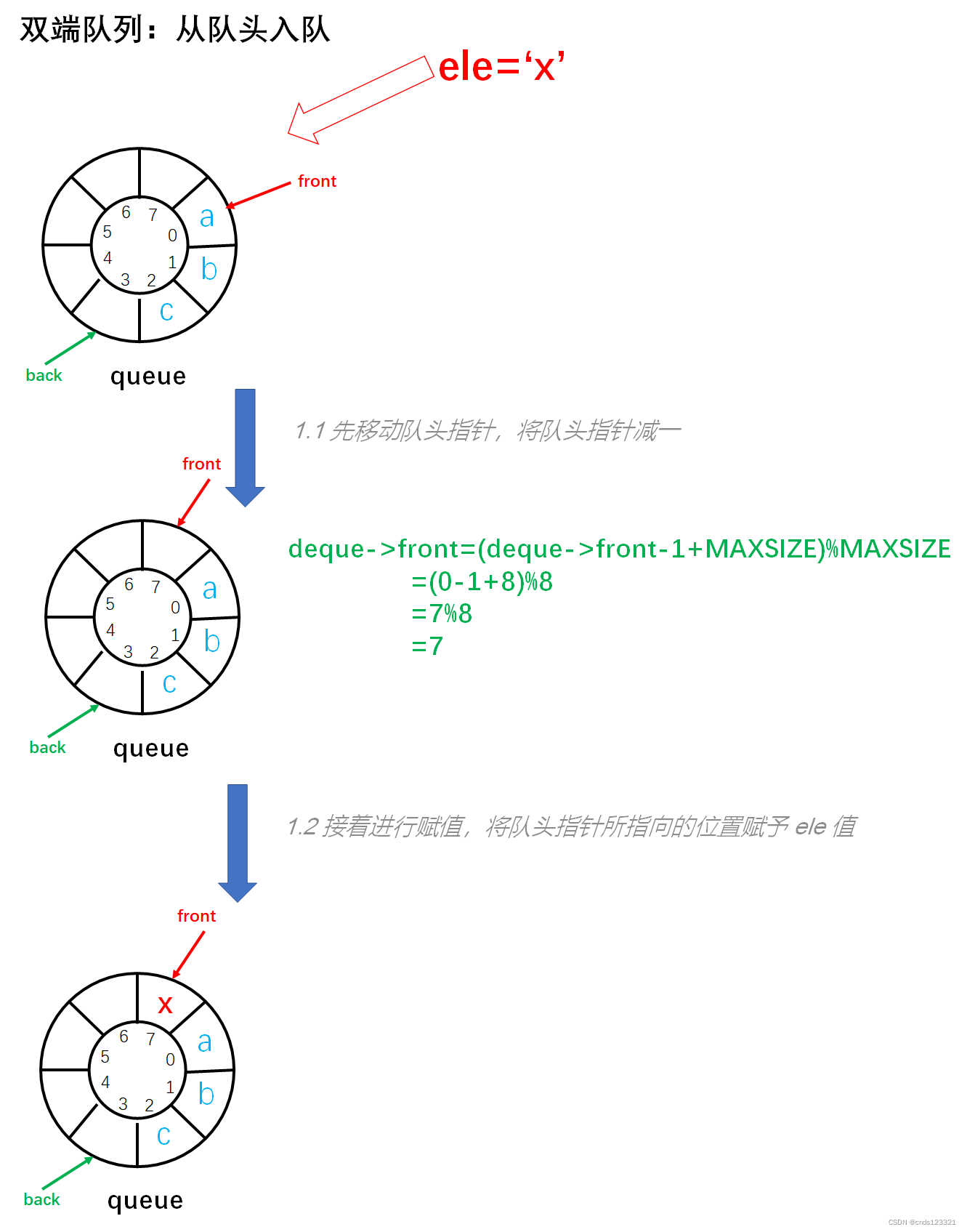
实现步骤：

• 参数校验，如果队满则不能入队。返回 0 表示入队失败。
• 先移动队头指针，将队头指针减一，但不是单纯的减一。因为队头指针始终指向队头元素，所以如果要从队头入队，那么队头指针要先指向一个可以存放元素的位置，只能向前移动，所以要减一。但是是循环队列，不能单纯的减一，如果 front==0 那么减一就会变成 -1，而下标没有 -1，所以要移动到数组的倒数第一个位置，即 MAXSIZE-，通过对 MAXSIZE 取余就会实现这种自动转换。
• 接着进行赋值，将队头指针所指向的位置赋予 ele 值。使得队头指针始终指向队头元素。
• 返回 1 表示入队成功。

实现代码如下：

/**
 * 从队头将元素入队
 * @param queue 双端队列
 * @param ele 待入队的元素
 * @return 如果队列已满则不能入队返回 0 表示入队失败；否则返回 1 表示入队成功
 */
int pushFront(DoubleEndedQueue *deque, int ele) {
    // 0.参数校验，如果队满则不能入队
    if (isFull(*deque)) {
        return 0;
    }

    // 1.将元素插入到队列的头部
    // 1.1 由于队头指针指向队列的队头元素，所以先修改队头指针。新元素应该插入到原队头元素的前面，所以要队头指针减一，因为是循环队列，所以要对 MAXSIZE 取余
    deque->front = (deque->front - 1 + MAXSIZE) % MAXSIZE;
    // 1.2 再对队头指针所指向的位置进行赋值
    deque->data[deque->front] = ele;
    // 1.3 返回 1 表示入队成功
    return 1;
}

pushBack

从队尾将元素入队。如果队未满才能入队，否则返回 0 表示入队失败。如果入队成功则返回 1。普通队列就是从队尾入队的，所以下面的图以及代码同循环队列的 enQueue 方法是一致的。以 deque=[a, b, c]; ele=x 为例如图：

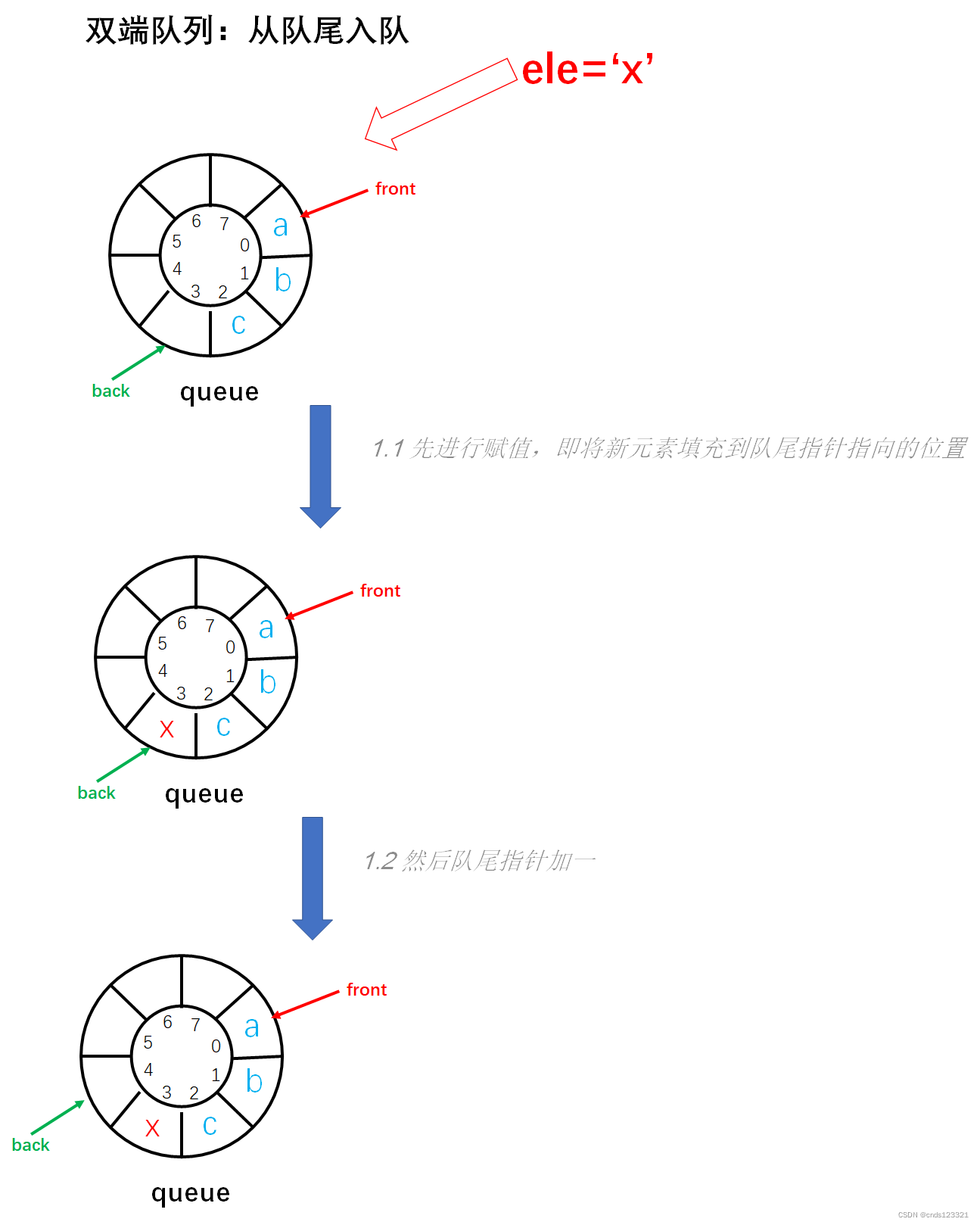
实现步骤：

• 参数校验，如果队满则不能入队。返回 0 表示入队失败。
• 先进行赋值，将队尾指针所指向的位置赋予 ele 值。
• 接着队尾指针加一，指向队尾元素的下一个位置。保证队尾指针始终指向队尾元素的下一位置。
• 返回 1 表示入队成功。

实现代码如下：

/**
 * 从队尾将元素入队
 * @param queue 双端队列
 * @param ele 待入队的元素
 * @return 如果队列已满则不能入队返回 0 表示入队失败；否则返回 1 表示入队成功
 */
int pushBack(DoubleEndedQueue *deque, int ele) {
    // 0.参数校验，如果队满则不能入队
    if (isFull(*deque)) {
        return 0;
    }

    // 1.将元素插入到队列的尾部
    // 1.1 由于队尾指针指向队尾元素的下一个位置，所以直接赋值即可
    deque->data[deque->back] = ele;
    // 1.2 插入元素后，需要移动队尾指针，将其加一，指向队尾元素的下一个位置，因为是循环队列，所以要对 MAXSIZE 取余
    deque->back = (deque->back + 1) % MAXSIZE;
    // 1.3 返回 1 表示入队成功
    return 1;
}

popFront

将元素从队头出队。如果队空则不能出队，返回 0 表示出队失败；将出队元素保存到 ele，并返回 1 表示出队成功。普通队列就是从队头出队的，所以下面的图以及代码同循环队列的 deQueue 方法是一致的。以 deque=[a, b, c, d, e, f, g] 为例如图所示：

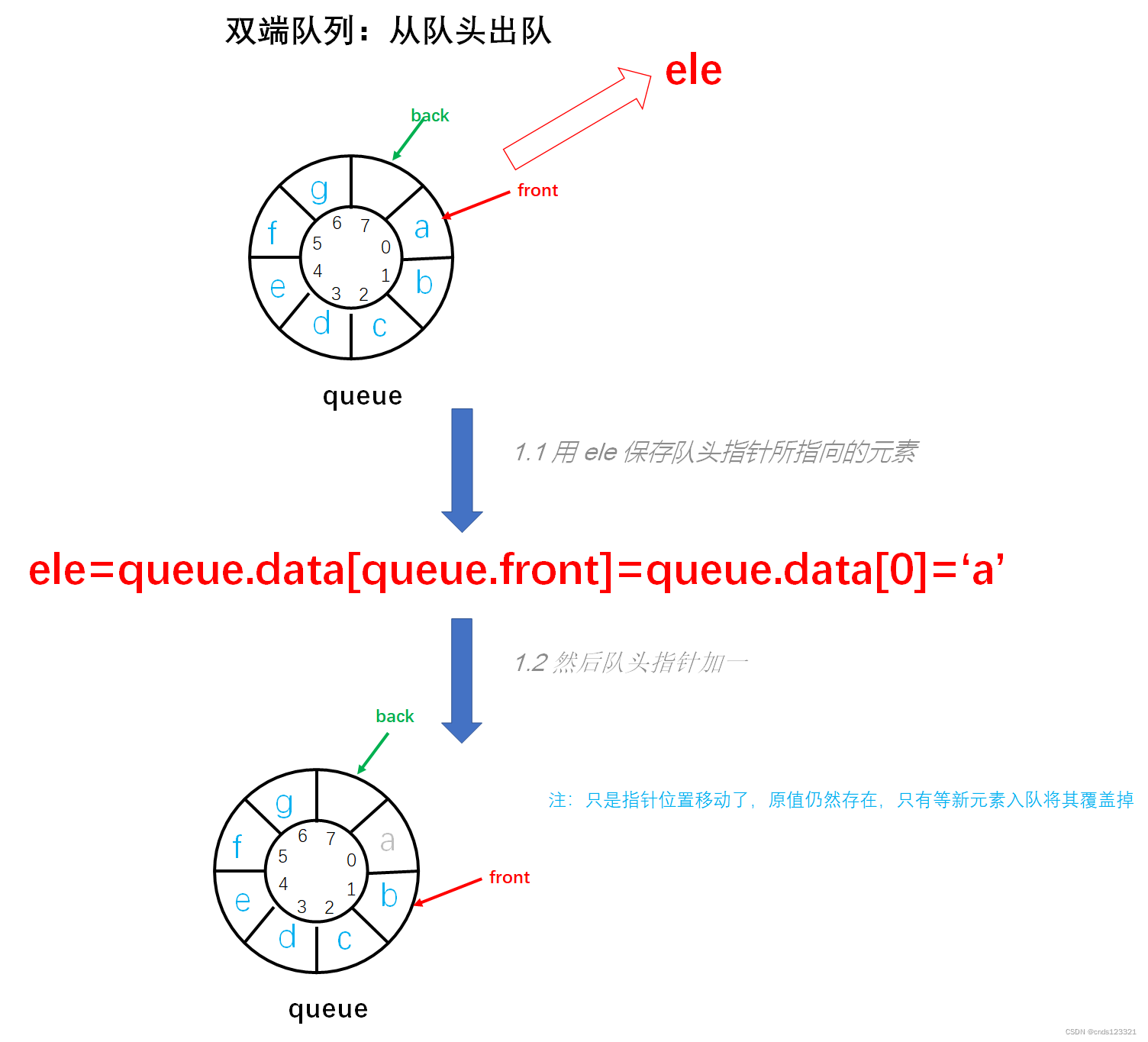
实现步骤：

• 参数校验，如果队空，则不能出队。返回 0 表示出队失败。
• 将元素出队。用 ele 保存队头指针所指向的元素。
• 然后将队头指针加一，保证队头指针始终指向队头元素。
• 返回 1 表示出队成功。

实现代码如下：

/**
 * 从队头将元素出队
 * @param deque 双端队列
 * @param ele 用来保存出队元素
 * @return 如果队空则返回 0 表示出队失败，否则返回 1 表示出队成功
 */
int popFront(DoubleEndedQueue *deque, int *ele) {
    // 0.参数校验，如果队空则不能出队
    if (isEmpty(*deque)) {
        return 0;
    }

    // 1.将队头元素出队
    // 1.1 用 ele 保存队头指针所指向的元素，即队头元素
    *ele = deque->data[deque->front];
    // 1.2 修改队头指针，将其加一，表示删除队头元素。因为是循环队列，所以要对 MAXSIZE 取余
    deque->front = (deque->front + 1) % MAXSIZE;
    // 1.3 返回 1 表示出队成功
    return 1;
}

popBack

从队尾将元素出队。如果队空则不能出队，返回 0 表示出队失败；将出队元素保存到 ele，并返回 1 表示出队成功。以 deque=[a, b, c, d, e, f, g] 为例如图所示：

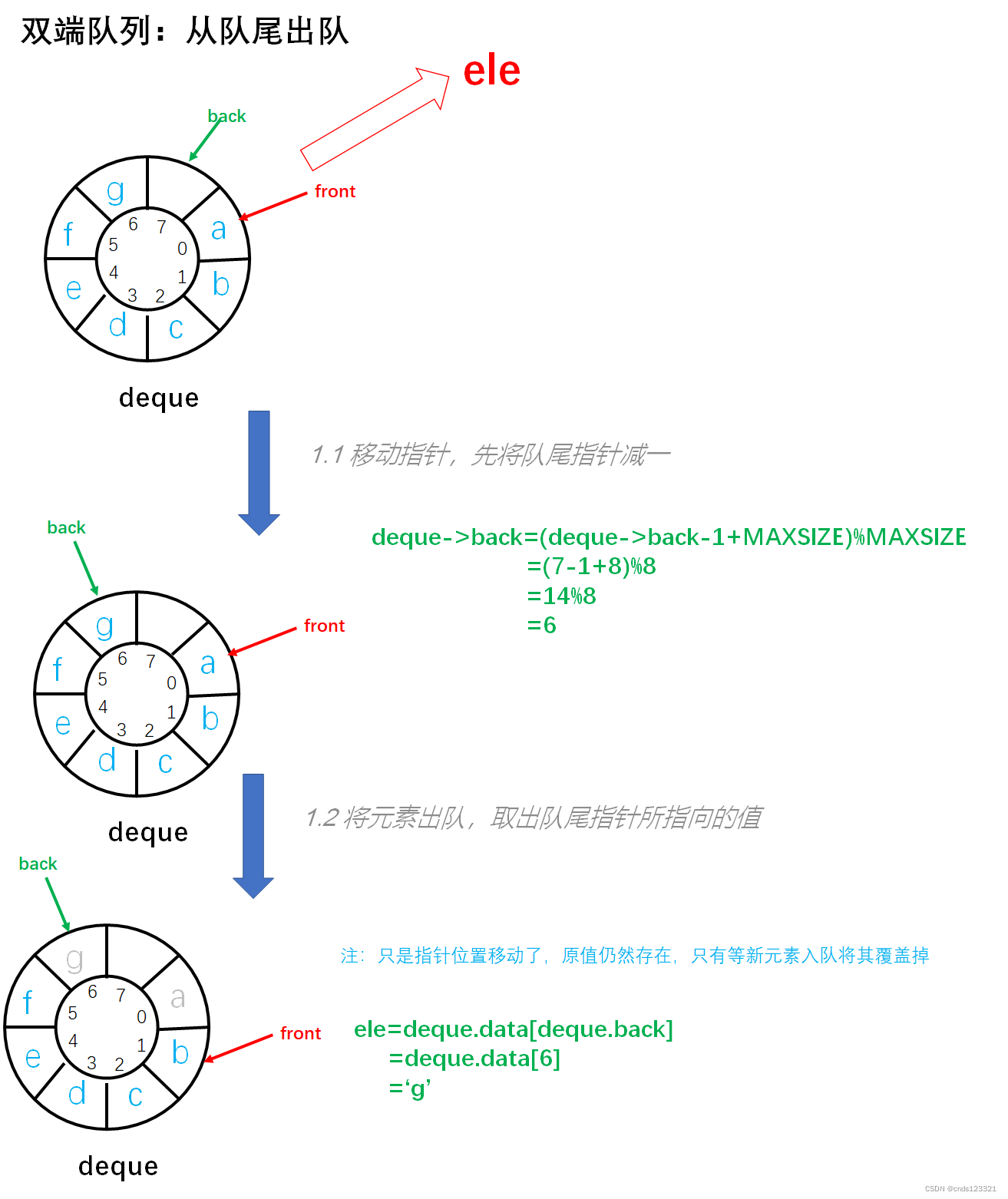
实现步骤：

• 参数校验，如果队空，则不能出队。返回 0 表示出队失败。
• 移动指针，先将队尾指针减一。由于队尾指针始终指向队尾元素的下一个位置，所以如果要获取到队尾元素，必须让队尾指针减一。但由于是循环队列，所以要对 MAXSIZE 取余。
• 将元素出队，取出队尾指针所指向的值。此时队尾指针所指向的值在出队后就是无效的元素了，因为队尾指针仍然要保持指向队尾元素的下一个位置。
• 返回 1 表示出队成功。

实现代码如下：

/**
 * 从队尾将元素出队
 * @param deque 双端队列
 * @param ele 用来保存出队元素
 * @return 如果队空则返回 0 表示出队失败，否则返回 1 表示出队成功
 */
int popBack(DoubleEndedQueue *deque, int *ele) {
    // 0.参数校验，如果队空则不能出队
    if (isEmpty(*deque)) {
        return 0;
    }
    // 1.从队尾将元素出队
    // 1.1 由于队尾指针指向队尾元素的下一个位置，所以先修改队尾指针，将其减一，但由于是循环队列，所以要对 MAXSIZE 取余
    deque->back = (deque->back - 1 + MAXSIZE) % MAXSIZE;
    // 1.2 然后取出当前队尾指针所指向的元素，就是待出队的元素
    *ele = deque->data[deque->back];
    // 1.3 返回 1 表示出队成功
    return 1;
}

size

获取双端队列中实际的元素个数。实际上就是获取循环队列的元素个数。

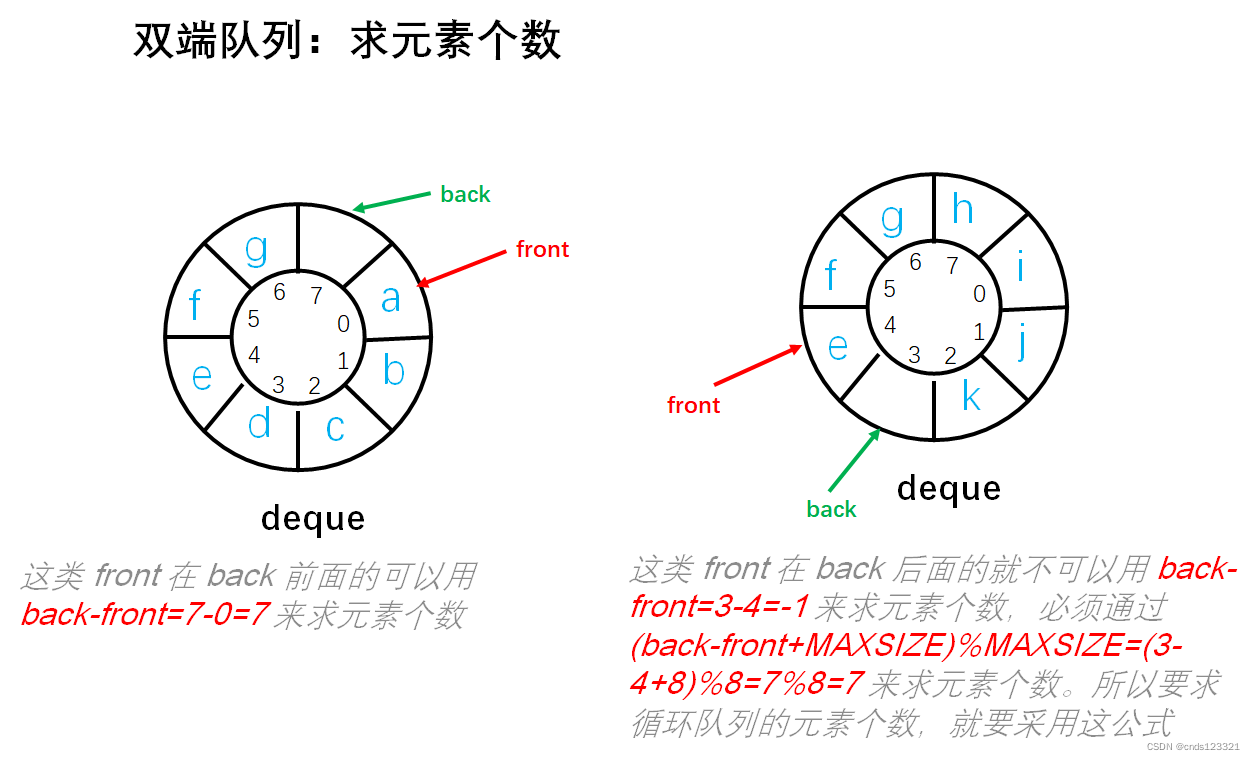
实现步骤：

• 循环队列的元素个数即 (back-front+MAXSIZE)%MAXISZE。

实现代码如下：

/**
 * 获取双端队列中的元素个数
 * @param deque 双端队列
 * @return 队列中的元素个数
 */
int size(DoubleEndedQueue deque) {
    // 如果是顺序队列，则元素个数是 rear-front
    // 如果是循环队列，则元素个数是 (rear-front+MAXSIZE)%MAXSIZE
    return (deque.back - deque.front + MAXSIZE) % MAXSIZE;
}

getFront

读取队头元素，但并不出队。如果队空则不能读取，则返回 0，否则用 ele 保存队头元素，返回 1 表示读取成功。

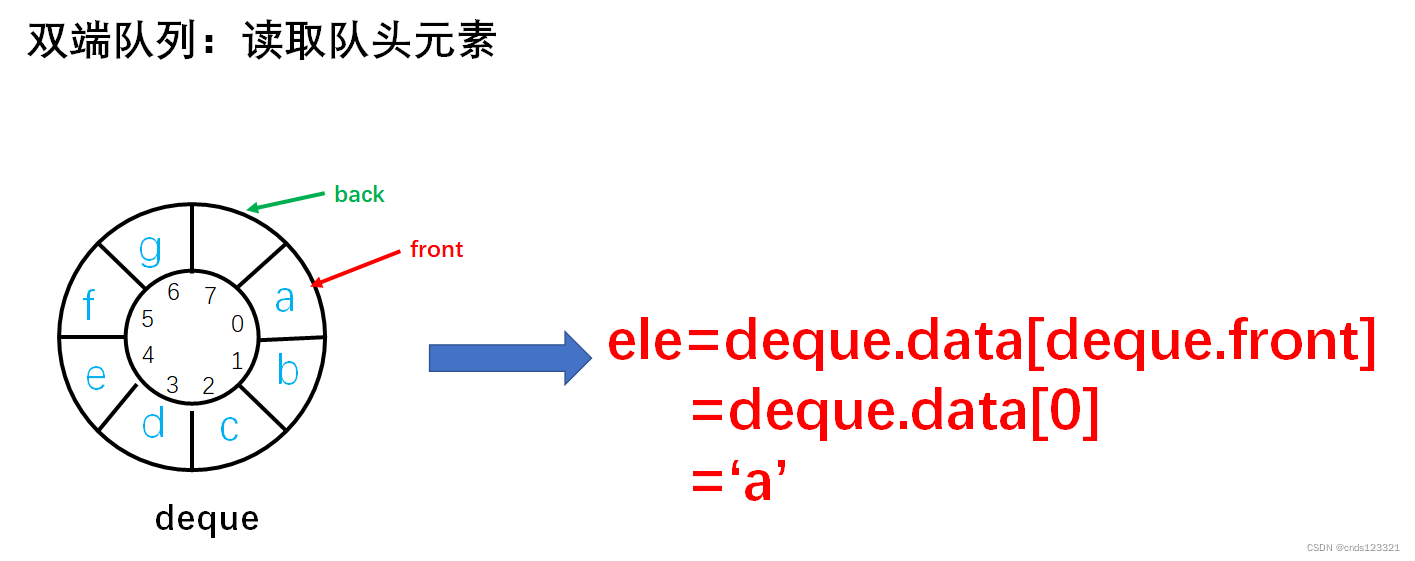
实现步骤：

• 参数校验，如果队空则没有队头元素，自然也无法获取。返回 0 表示读取失败。
• 直接读取队头指针所指向的元素。因为队头指针始终指向队头元素。

实现代码如下：

/**
 * 获取双端队列的队头元素
 * @param deque 双端队列
 * @param ele 用来保存队头元素
 * @return 如果出队成功则返回 1，否则返回 0 表示出队失败
 */
int getFront(DoubleEndedQueue deque, int *ele) {
    // 0.参数校验，如果队列为空则不能获取队头元素
    if (isEmpty(deque)) {
        return 0;
    }
    // 1.用 ele 保存队头指针所指向的元素
    *ele = deque.data[deque.front];
    return 1;
}

getBack

读取双端队列的队尾元素。如果双端队空为空则返回 0 表示读取失败。否则用 ele 保存队尾元素，并返回 1 读取成功。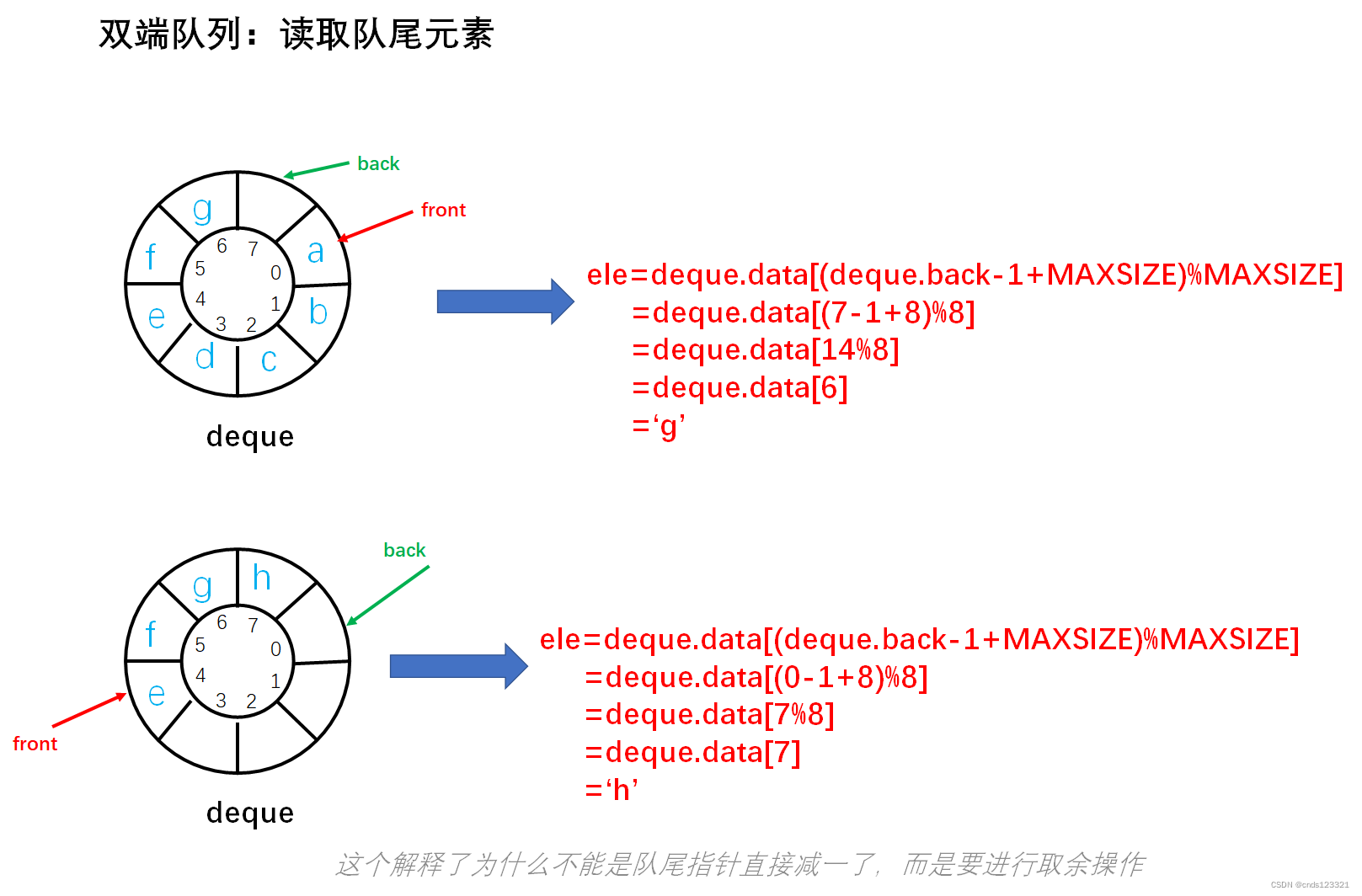

实现步骤：

• 参数校验，如果队空，则不能读取队尾元素。返回 0 表示读取失败。
• 读取队尾指针所指向位置的前一个位置的元素，用 ele 保存。因为队尾指针始终指向队尾元素的下一个位置，所以要读取队尾元素，需要读取到队尾指针的前一个位置的元素。但并不是队尾指针单纯的减一，因为是循环队列。
• 返回 1 表示读取成功。

实现代码如下：

/**
 * 获取双端队列的队尾元素
 * @param deque 双端队列
 * @param ele 用来保存队尾元素
 * @return 如果出队成功则返回 1，否则返回 0 表示出队失败
 */
int getBack(DoubleEndedQueue deque, int *ele) {
    // 0.参数校验，如果队列为空则不能获取队尾元素
    if (isEmpty(deque)) {
        return 0;
    }
    // 1.用 ele 保存队尾指针所指向的前一个元素，因为队尾指针指向队尾元素的下一个位置，所以要减一，因为是循环队列，所以要对 MAXSIZE 取余
    *ele = deque.data[(deque.back - 1 + MAXSIZE) % MAXSIZE];
    return 1;
}

clear

清空双端队列。实际上是清空循环队列。

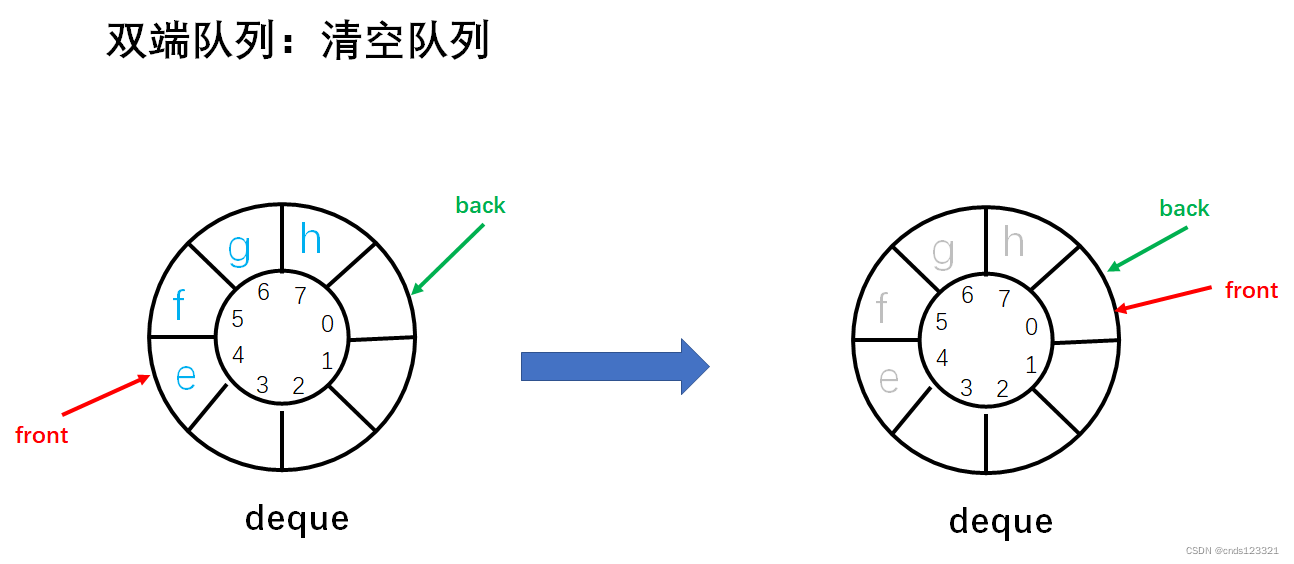
实现步骤：

• 将双端队列的队头指针 front 和队尾指针 back 都指向 0，表示空队列。但实际上队列中原有的元素仍然存在，并没有被重置为某个值。

实现代码如下：

/**
 * 清空双端队列
 * @param deque 双端队列
 */
void clear(DoubleEndedQueue *deque) {
    // 即将队头指针和队尾指针指向 0，表示空队列
    deque->front = 0;
    deque->back = 0;
}

print

打印双端队列中的所有有效元素。

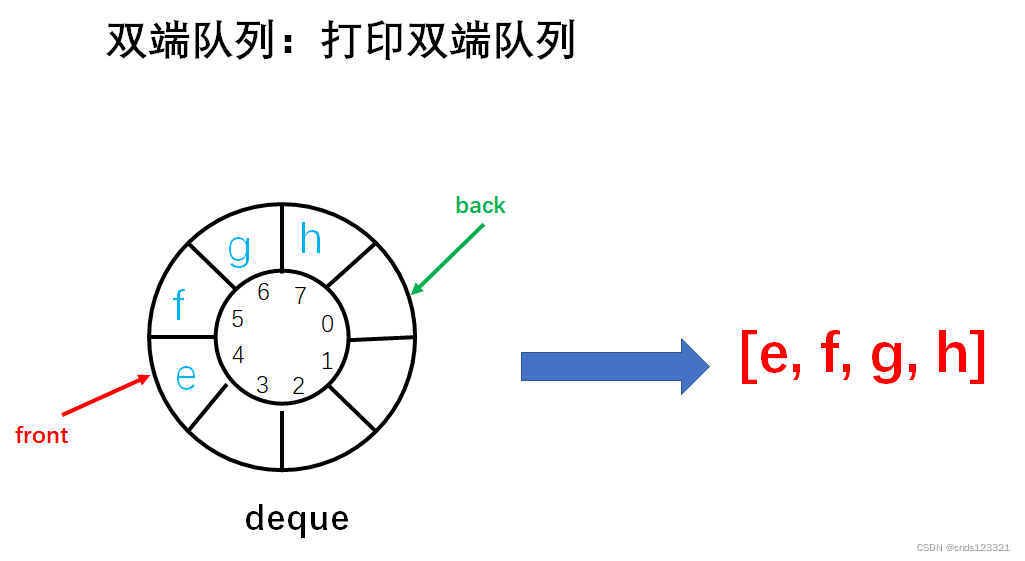
实现步骤：

• 从队头指针开始扫描整个双端队列，直到队尾指针结束，但不包括队尾指针所指向的元素。

实现代码如下：

/**
 * 打印双端队列从队头到队尾的所有元素
 * @param deque 双端队列
 */
void print(DoubleEndedQueue deque) {
    printf("[");
    int front = deque.front;
    while (front != deque.back) {
        printf("%d", deque.data[front]);
        if (front != (deque.back - 1 + MAXSIZE) % MAXSIZE) {
            printf(", ");
        }
        front = (front + 1) % MAXSIZE;
    }
    printf("]\n");
}

注意事项

无。

练习题

• Example003-如果允许在循环队列的两端都可以进行插入和删除操作，分别写出从队尾删除和从队头插入的算法