一、前言

学习完string类之后，我们在来学习vector难度并没有之前那么高，更加容易理解一些接口

vector是表示可变大小数组的序列容器 ，本质讲，vector使用动态分配数组来存储它的元素。

同理，对于vector的使用，我们也要学会去看文档：vector官方文档

本文重点只介绍一些常用的接口

---

二、构造函数

构造函数的具体介绍直接前往官网查看文档即可，这里只做简单介绍：

(constructor)构造函数声明	接口说明
vector()	无参构造
vector（size_type n, const value_type& val = value_type())	构造并初始化n个val
vector (const vector& x);	拷贝构造
vector (InputIterator first, InputIterator last);	使用迭代器进行初始化构造

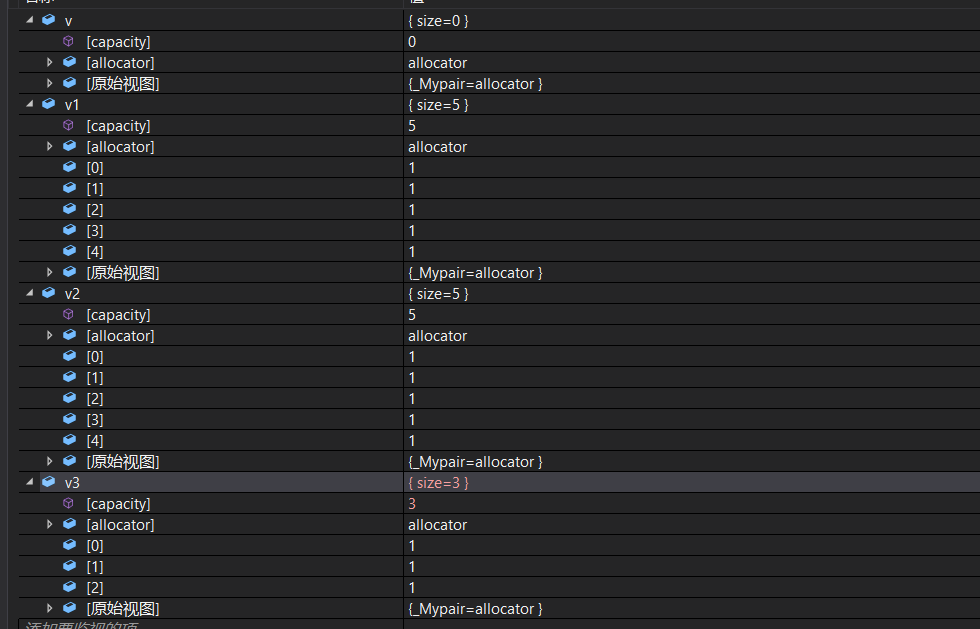
对于构造函数，这些与string类似，我们就不在多说，直接上手代码：

void Test()
{
	vector<int> v;//无参构造
	vector<int> v1(5, 1);//构造并初始5个1
	vector<int> v2(v1);//拷贝构造
	vector<int> v3(++v1.begin(), --v1.end());//迭代器初始化构造
}

此外，对于vector和string的关系是无法替代的，string类中有一个接口c_str()，转化成C语言的字符串要以\0结尾，所以string类最后会有一个\0,在操作上+=,<<,>>等。而vector是保存字符的动态数组，不会以\0结尾，不保存\0，且vector是T泛型，所以并不存在谁替代谁。

---

三、遍历

1.[]

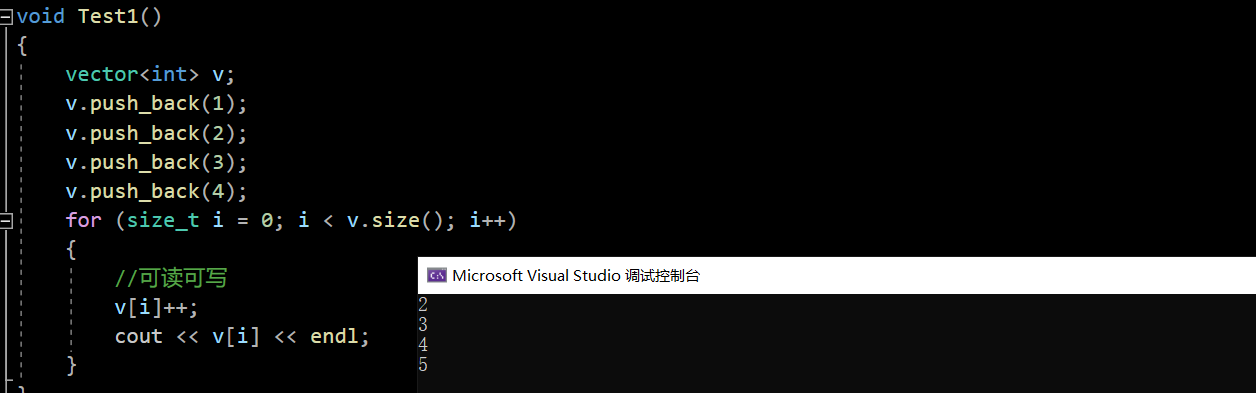
void Test1()
{
	vector<int> v;
	v.push_back(1);
	v.push_back(2);
	v.push_back(3);
	v.push_back(4);
	for (size_t i = 0; i < v.size(); i++)
	{
		//可读可写
		v[i]++;
		cout << v[i] << endl;
	}
}

2.迭代器、范围for()

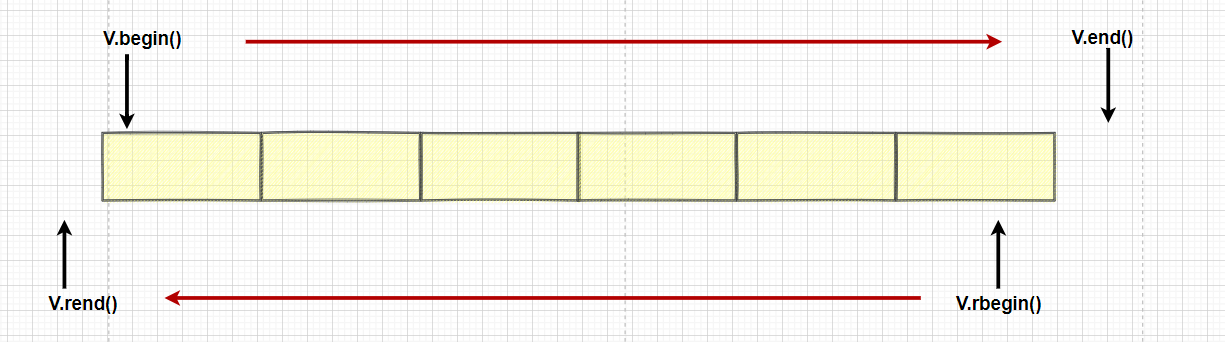
正向迭代器和反向迭代器

iterator的使用	接口说明
begin + end	获取第一个数据位置的iterator/const_iterator， 获取最后一个数据的下一个位置 的iterator/const_iterator
rbegin + rend	获取最后一个数据位置的reverse_iterator，获取第一个数据前一个位置的 reverse_iterator

void Test2()
{
	vector<int> v;
	v.push_back(1);
	v.push_back(2);
	v.push_back(3);
	v.push_back(4);
	
	vector<int>::iterator it = v.begin();
	while (it != v.end())
	{
		(*it)++;
		cout << *it << " ";
		it++;
	}
	cout << endl;

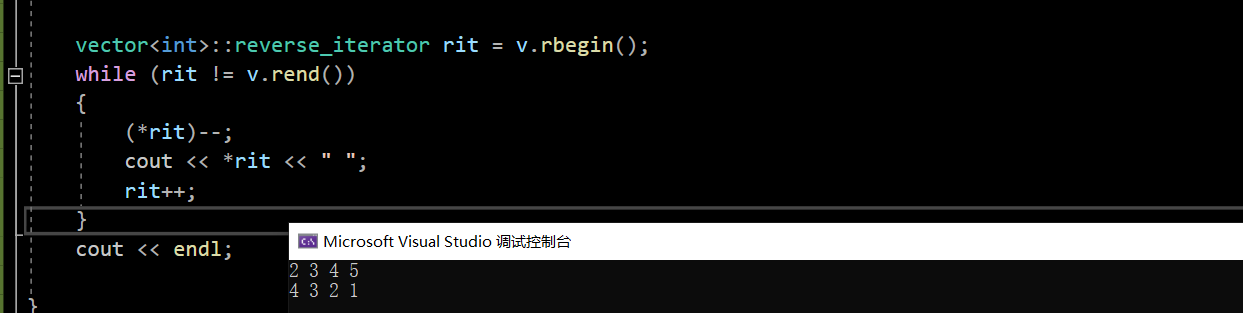
	vector<int>::reverse_iterator rit = v.rbegin();
	while (rit != v.rend())
	{
		(*rit)--;
		cout << *rit << " ";
		rit++;
	}
	cout << endl;

}

迭代器很自然和范围for联系起来：

for (auto e : v)
{
	cout << e << " ";
}
cout << endl;

---

四、增删查改

1.常用接口

容量空间	接口说明
size	获取数据个数
capacity	获取容量大小
empty	判断是否为空
resize	改变vector的size
reserve	改变vector放入capacity

resize&&reserve&&扩容问题

前三个比较容易理解，我们就不说了，我们直接来看resize

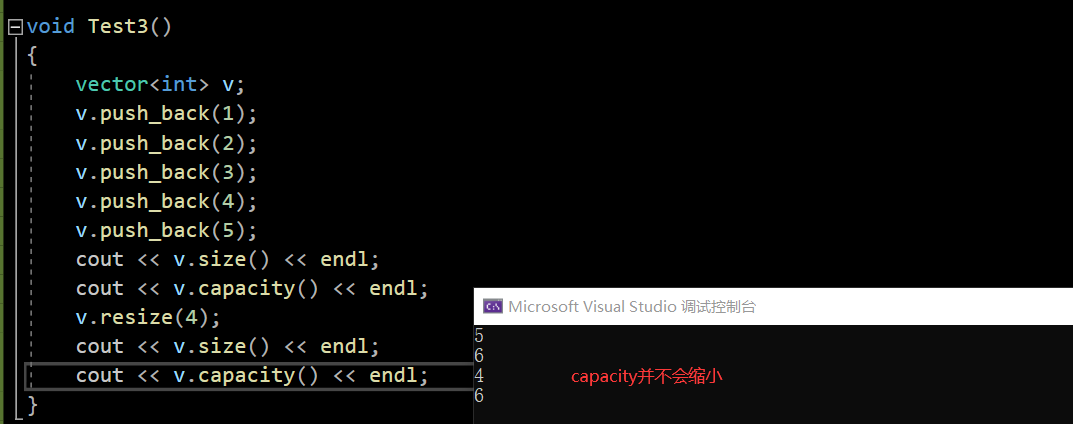
void Test3()
{
	vector<int> v;
	v.push_back(1);
	v.push_back(2);
	v.push_back(3);
	v.push_back(4);
	v.push_back(5);
	cout << v.size() << endl;
	cout << v.capacity() << endl;
	v.resize(4);
	cout << v.size() << endl;
	cout << v.capacity() << endl;
}

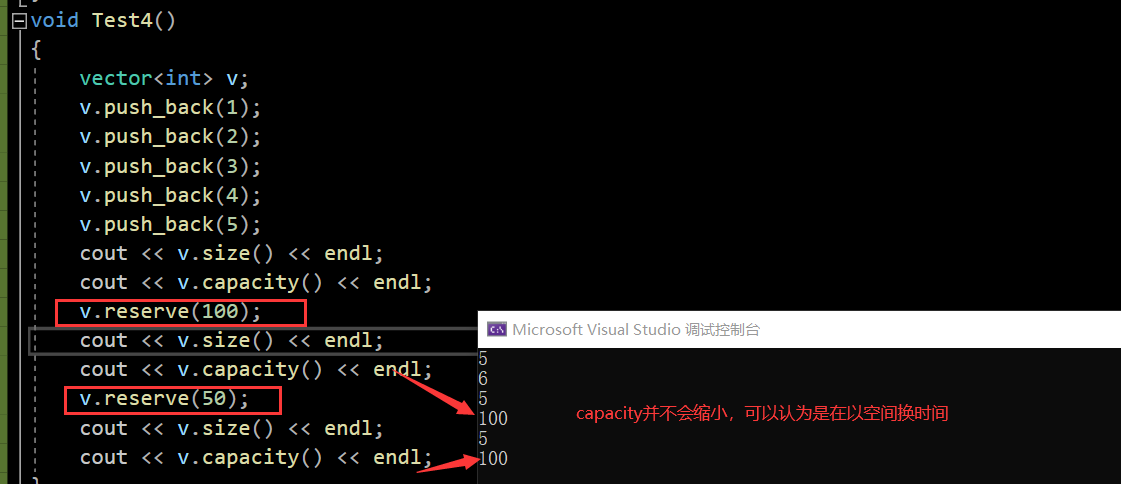
对于reserve:

void Test4()
{
	vector<int> v;
	v.push_back(1);
	v.push_back(2);
	v.push_back(3);
	v.push_back(4);
	v.push_back(5);
	cout << v.size() << endl;
	cout << v.capacity() << endl;
	v.reserve(100);
	cout << v.size() << endl;
	cout << v.capacity() << endl;
	v.reserve(50);
	cout << v.size() << endl;
	cout << v.capacity() << endl;
}

capacity扩容问题：

capacity的代码在vs和g++下分别运行会发现，vs下capacity是按1.5倍增长的，g++是按2倍增长的

void Test5()
{
	size_t sz;
	std::vector<int> foo;
	sz = foo.capacity();
	std::cout << "making foo grow:\n";
	for (int i = 0; i < 100; ++i) {
		foo.push_back(i);
		if (sz != foo.capacity()) {
			sz = foo.capacity();
			std::cout << "capacity changed: " << sz << '\n';
		}
	}
}

VS下：

Linux的g++下：

2.增删查改

vector增删查改	接口说明
push_back	尾插
pop_back	尾删
find	查找。（注意这个是算法模块实现，不是vector的成员接口）
insert	在position之前插入val
erase	删除position位置的数据
swap	交换两个vector的数据空间

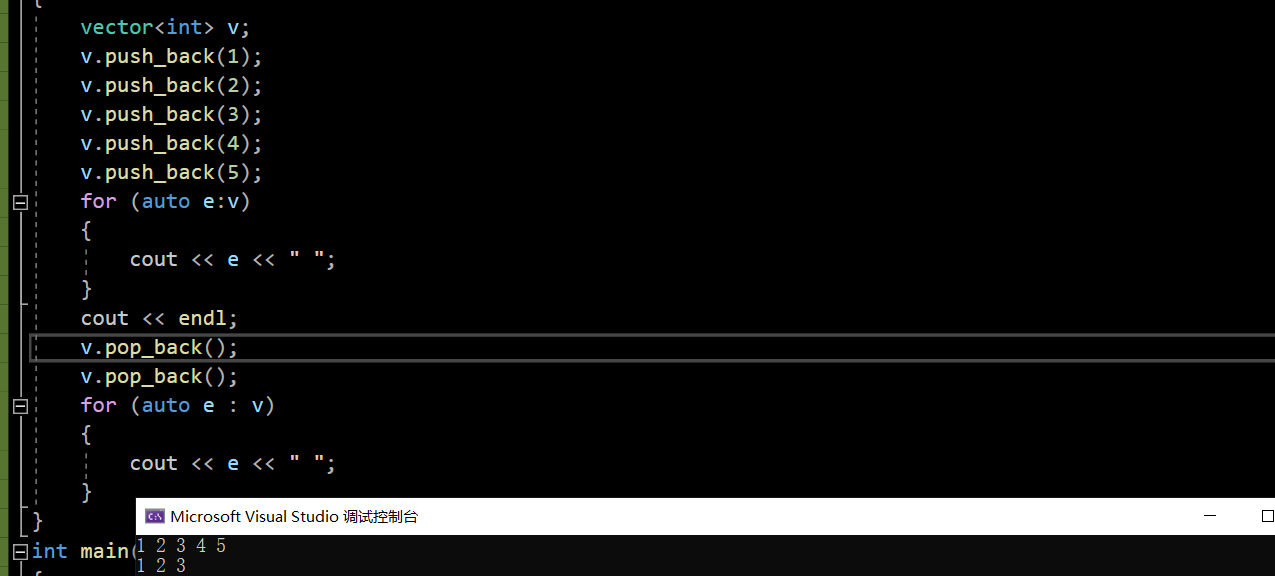
1.push_back和pop_back的用法比较简单：

void Test6()
{
	vector<int> v;
	v.push_back(1);
	v.push_back(2);
	v.push_back(3);
	v.push_back(4);
	v.push_back(5);
	for (auto e:v)
	{
		cout << e << " ";
	}
	cout << endl;
	v.pop_back();
	v.pop_back();
	for (auto e : v)
	{
		cout << e << " ";
	}
}

2.find

注意：算法库中给我们提供一个模板，vector本身并没有find接口，下面我们来看一看：

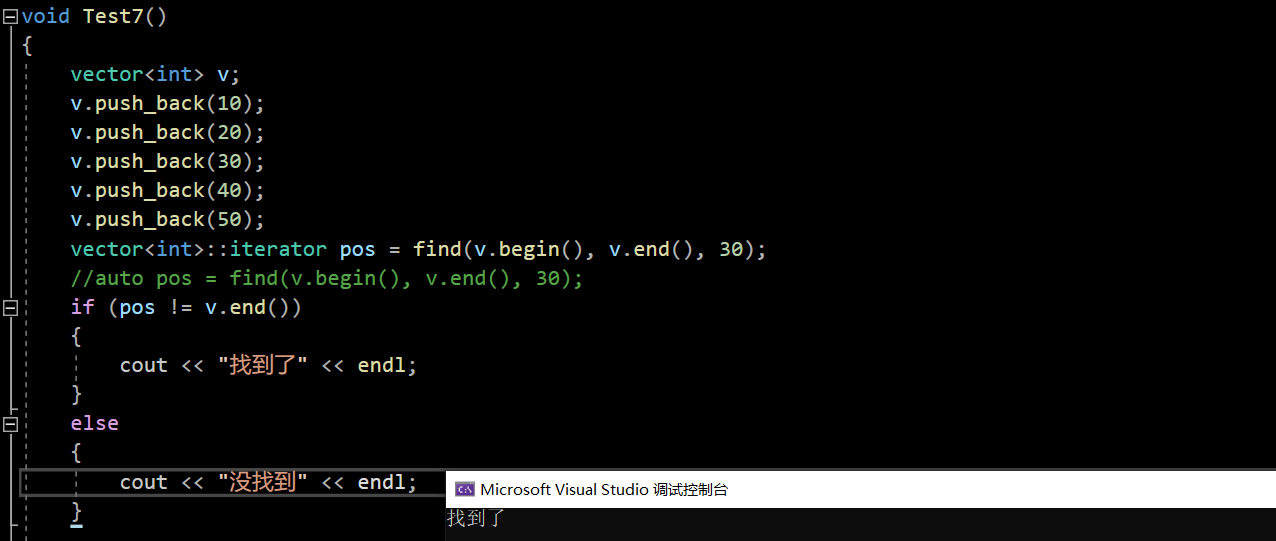
void Test7()
{
	vector<int> v;
	v.push_back(10);
	v.push_back(20);
	v.push_back(30);
	v.push_back(40);
	v.push_back(50);
	vector<int>::iterator pos = find(v.begin(), v.end(), 30);
	//auto pos = find(v.begin(), v.end(), 30);
	if (pos != v.end())
	{
		cout << "找到了" << endl;
	}
    else
    {
        cout<<"没找到"<<endl;
    }

}

3.insert和erase

这两个接口通常配合find使用。对于string的insert和erase支持下标，因为string的find刚好可以返回下标位置：

void Test8()
{
	vector<int> v;
	v.push_back(10);
	v.push_back(20);
	v.push_back(30);
	v.push_back(40);
	v.push_back(50);
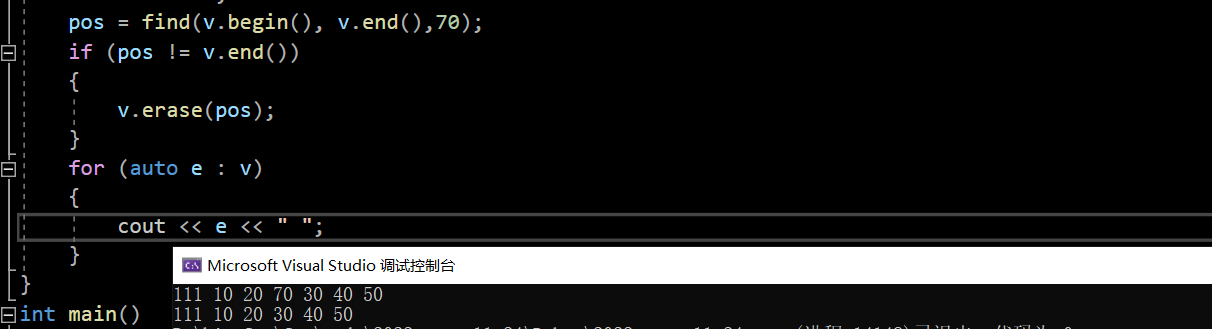
	v.insert(v.begin(), 111);
	vector<int>::iterator pos = find(v.begin(),v.end(), 30);
	if (pos != v.end())
	{
		v.insert(pos, 70);
	}
	for (auto e : v)
	{
		cout << e << " ";
	}
	cout << endl;
	pos = find(v.begin(), v.end(),70);
	if (pos != v.end())
	{
		v.erase(pos);
	}
	for (auto e : v)
	{
		cout << e << " ";
	}
}

4.swap

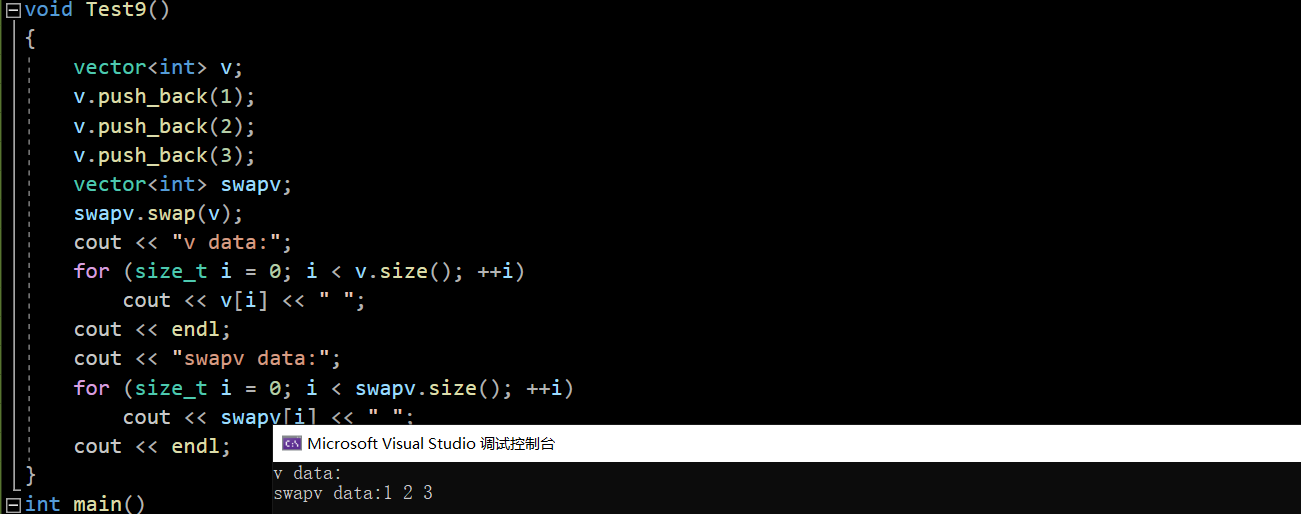
void Test9()
{
	vector<int> v;
	v.push_back(1);
	v.push_back(2);
	v.push_back(3);
	vector<int> swapv;
	swapv.swap(v);
	cout << "v data:";
	for (size_t i = 0; i < v.size(); ++i)
		cout << v[i] << " ";
	cout << endl;
	cout << "swapv data:";
	for (size_t i = 0; i < swapv.size(); ++i)
		cout << swapv[i] << " ";
	cout << endl;
}

---

对于vector的基本使用我们就先说到这里，下面进入我们的题目练习。

五、经典题目

#include <iostream>
#include <vector>
using namespace std;
int main(void)
{
	vector<int>array;
	array.push_back(100);
	array.push_back(300);
	array.push_back(300);
	array.push_back(300);
	array.push_back(300);
	array.push_back(500);
	vector<int>::iterator itor;
	for (itor = array.begin(); itor != array.end(); itor++)
	{
		if (*itor == 300)
		{
			itor = array.erase(itor);
		}
	}
	for (itor = array.begin(); itor != array.end(); itor++)
	{
		cout << *itor << " ";
	}
	return 0;
}

程序首先把100 300 300 300 300 500进行尾插

数据为300时进行删除,同时itor指向下一个元素，但是由于循环回去，for循环末尾itor++会让迭代器指向下一个。

所以只删除了2个值为300的元素，所以答案为100 300 300 500

1.杨辉三角

[118. 杨辉三角](118. 杨辉三角 - 力扣（Leetcode）)

此题用C语言做起来非常麻烦，但是用vector来做就变得更简单了：

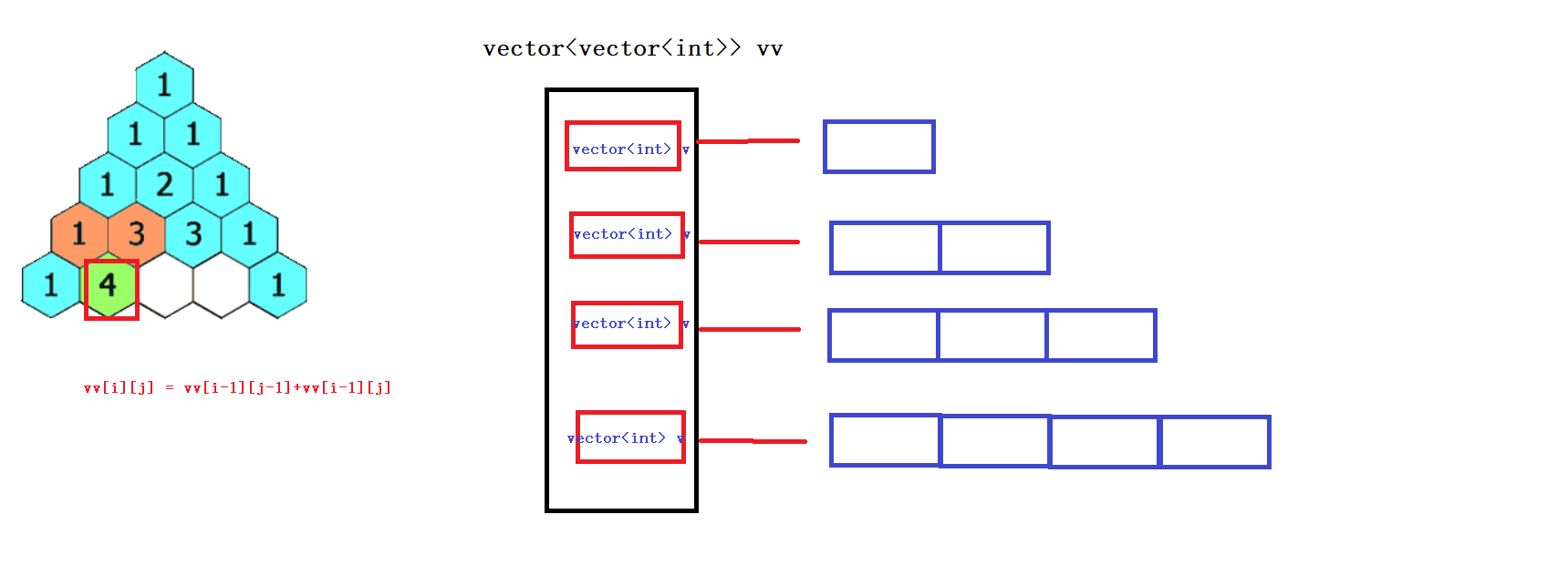
每行的头和尾都是1，其他的第[j]个=上一行的第[j-1]+[j]

class Solution {
public:
    vector<vector<int>> generate(int numRows) {
        vector<vector<int>> vv;
        vv.resize(numRows);
        for(size_t i = 0;i<vv.size();i++)
        {
            vv[i].resize(i+1,0);
            vv[i][0] = vv[i][vv[i].size()-1] = 1;
        }
        for(size_t i  = 0;i<vv.size();i++)
        {
            for(size_t j = 0;j<vv[i].size();j++)
            {
                if(vv[i][j] == 0)
                {
                    vv[i][j] = vv[i-1][j]+vv[i-1][j-1];
                }
            }
        }
        return vv;
    }
};

2.电话号码组合

[17. 电话号码的字母组合](17. 电话号码的字母组合 - 力扣（Leetcode）)

此题适合采用回溯的做法，可以先定义一个数组进行映射，确定回溯函数参数，确定终止条件，确定单层的逻辑即可解决：

class Solution {
    private:
    const string letterMap[10] = 
    {" "," ","abc","def","ghi","jkl","mno","pqrs","tuv","wxyz"};
    string s;
    vector<string> result;
    void backtracking(const string&digits,int index)
    {
        if(index == digits.size())
        {
            result.push_back(s);
            return;
        }
        int digit = digits[index]-'0';
        string letter = letterMap[digit];
        for(int i = 0;i<letter.size();i++)
        {
            s.push_back(letter[i]);
            backtracking(digits,index+1);
            s.pop_back();
        }
    }
public:
    vector<string> letterCombinations(string digits) {
        s.clear();
        result.clear();
        if(digits.size()==0)
        {
            return result;
        }
        backtracking(digits,0);
        return result;
    }
};

3.只出现一次的数ii

137. 只出现一次的数字 II

除某个元素仅出现 一次 外，其余每个元素都恰出现 三次

对于这道题目，我们可以统计所有数字的二进制的各个位之和，每一个元素都出现了 3 次，对应着第 i 个二进制位的 3 个 0或 3 个 1，无论是哪一种情况，出现三次的数字相加起来就是3的倍数，所以最终只需要模3即可：

class Solution {
public:
    int singleNumber(vector<int>& nums) {
        int ret = 0;
        for(int i = 0;i<32;i++)
        {
            int sum = 0;
            for(auto& e:nums)
            {
                sum+=(e>>i)&1;
            }
            sum%=3;
            ret+=(sum<<i);
        }
        return ret;
    }
};

4.只出现一次的数字 III

260. 只出现一次的数字 III

其中恰好有两个元素只出现一次，其余所有元素均出现两次.

把整个数组异或之后就值剩下那个只出现一次的元素，然后在找出这两个只出现一次元素的不同的二进制位

然后进行分组即可解决此题。

class Solution {
public:
    vector<int> singleNumber(vector<int>& nums) {
        vector<int> v;
        int ret = 0;
        //整个数组进行异或
        for(auto e:nums)
        {
            ret^=e;
        }
        //找出不同的二进制位
        int flag = 0;
        for(int i = 0;i<32;i++)
        {
            if((1&(ret>>i)) == 1)
            {
                flag = i;
                break;
            }
        }
        //进行分组异或
        int x1 = 0,x2 = 0;
        for(auto e: nums)
        {
            if((1&(e>>flag)) == 1)
            {
                x1^=e;
            }
            else
            {
                x2^=e;
            }
        }
        v.push_back(x1);
        v.push_back(x2);
        return v;
    }
};