导言:
我们在上一次学习了堆栈的数据结构以后,可以了解到它是受限制的操作,比如我们操作只能在栈顶,现在我们要学习的东西叫做队列,它也是受限制的一种数据结构,它的特点是队头只出数据,而队尾只入数据,
它的结构就和它的名字,像我们平时排队一样先来的人肯定要先服务啊,所以它的英文叫做Frist In Frist Out 即 FIFO
一.顺序表实现队列
队列:具有一定约束的线性表
插入和删除操作:只能在一段插入,只能在另一端删除
实现队列我们需要根据它的特点来构建结构,比如它需要一个指针 front 指向队头,也需要一个指针 rear 指向队尾

这就是我们构建的主要的结构,用它构造的数组具有指向性,可以知道现在在哪里可以插入数据,在哪可以删除数据,都是实时记录位置的
我们来思考一下现在这么构造的数据结构,
首先,此队列能存放6个数据,然后它在用Data来记录真实的数据,使用font来记录队头,每次出队列都需要我们font指针向后移动一次,地址指针加一,同时使用rear来记录队尾,每次入队都在这里,它会在加一的情况后在进行入队
队头指向的多是空数据,而队尾指向的是新添的当前数据,它们指向的位置不一样,也就是说,一旦front指向的数据,如果此空间有数据,那么一定是出队列的,而rear指向的空间,一定是刚刚入队的数据
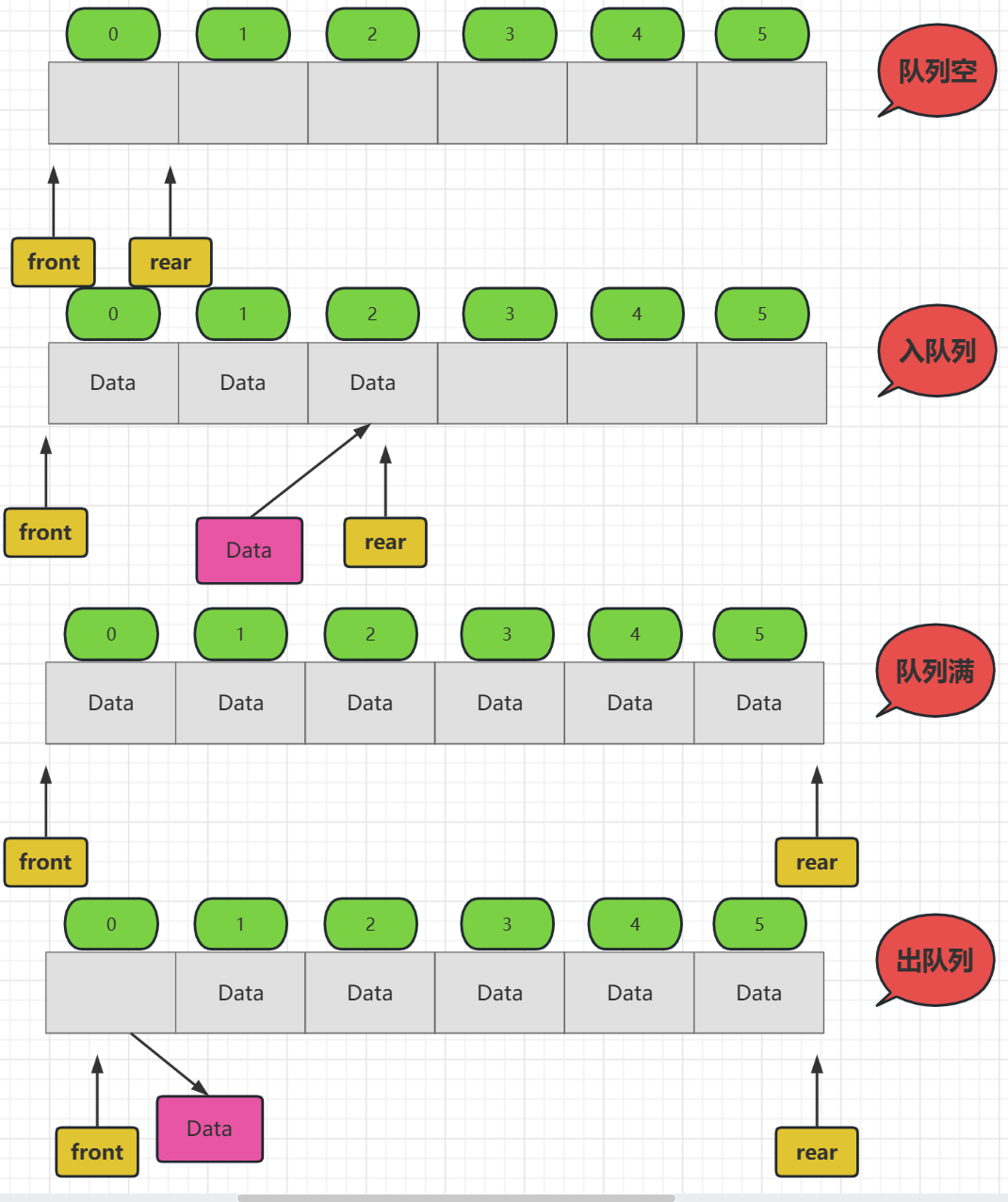
上面就是最开始我们设计的顺序表实现队列,看起来也十分简单,完美的利用了数组的特性,可是我们多使用几次就会发现,他有一个很明显的弊端,那就是经过几次入队列后会出现空间利用不充分的
比如我们在队列满了的情况下出队列几个数据,那么还能入队列吗?很显然不能,因为此时队尾指针 rear 已经指向 Maxsize 了,
所以,一般我们不会使用这种方式实现队列,空间利用率太低了,而是采用循环队列的方式去构造,别入rear到达Maxsize的时候,只要发现front不在 0 号位置,说明前面还有空间可以入队,就在前面入队
只要front和rear指针正常工作,循环队列是可以很简单的实现的
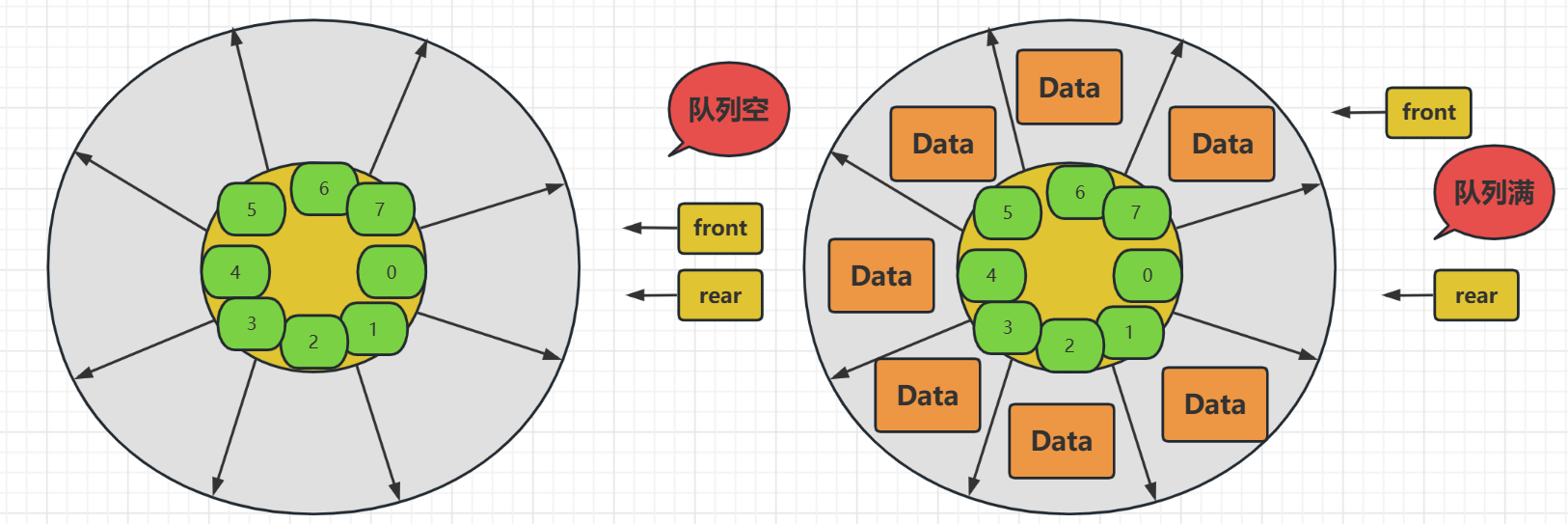
循环队列的设计就很合理,提高了数组空间的复用性,原本出队后就不能使用的空间这下也被利用起来了,只是我们在使用循环队列的时候要注意几个点
- 队列的下标不能只是当前下标直接加一了当为7的时候应该为0才能循环入队列,所以需要使用当前位置 + 1 取余 Maxsize
- 判断队列为空,初始的时候为空,即两个指针位置相同时为空,在是顺序表中的两个指针都指向 -1 才为空
- 如果为空是两指针位置相等那么,队列满还能使用两指针位置相等吗?和显然不能,因为真的两指针位置相等时不确定队列满还是空,所以我们使用front + 1 == rear来判定队列满,也就是说,其实我们是有一个空间未使用的,但也是必须的,这样解决方式是最高效的
下面入队列的伪代码实现
void InQueue(Queue Q,ElementType d){ if((Q->rear+1)%Maxsize == Q->front){ printf("队列满!"); return; } Q->rear=(Q->rear+1)%Maxsize; Q->Data[Q->rear]=d; }
下面是出队列的代码实现
ElementType OutQueue(Queue Q){ if(Q->front == Q->rear){ printf("队列空!"); return ERROR; } Q->front=(Q->front+1)%Maxsize; return Q->Data[Q->front]; // 直接返回,不需要清空刚刚的空间,会被移动覆盖 // 插入的条件不是当前单元有没有数据而是 front 是否等于 rear+1 }
大家可以思考,为什在出队列的时候直接返回就行了,而不用对此空间进行归零或者打上可插入的标记?
二.链表实现队列
队列的链表实现也可以使用一个单链表实现,插入和删除在两头进行,那么那一头来做队头,那部分做队尾呢?
链表的头部,肯定是做删除和新增操作都是没问题的,主要是是看链表尾部
对于链表尾部,它新增一个结点没有问题,直接指针指向那个结点就好了,但是做不了删除操作,
因为我们的实现方式是单链表,它是没有回头指针的,一旦尾部来执行删除操作,一定会使得我们找不到后面的元素,所以链表头部来做删除,链表尾部来做插入
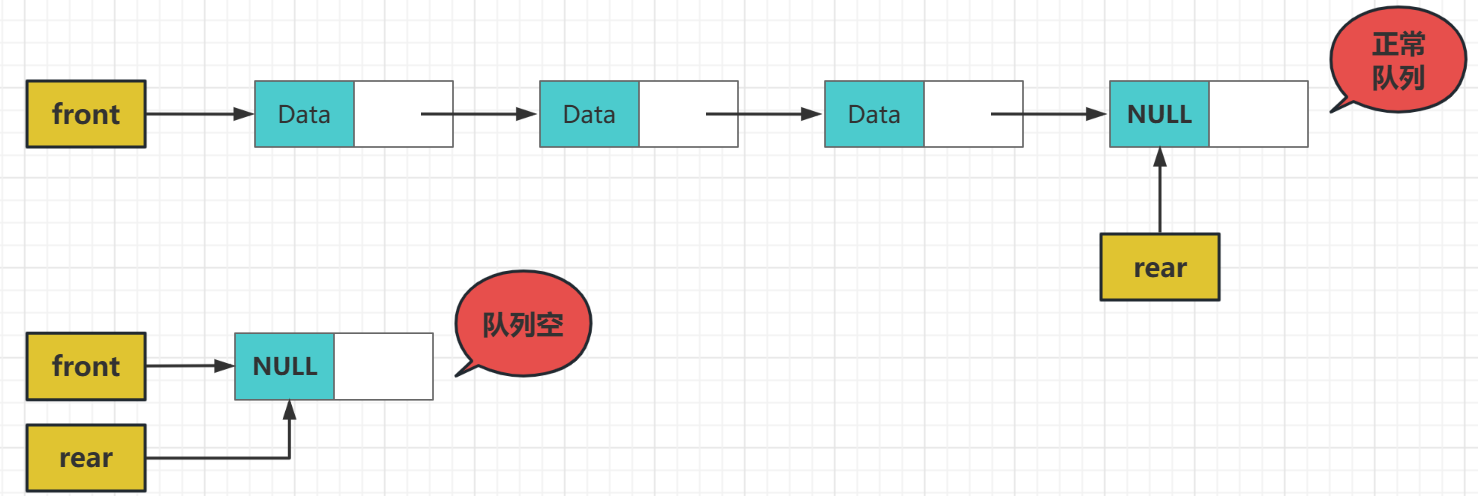
使用链表是没有满的情况的,除非内存被申请满了,不然就可以一直申请结点来装新的数据
使用链表还是那几个注意点:
- 删除结点的时候一定要释放空间,避免内存泄漏
- 新增结点通过动态开辟,然后队尾指针去指向
- 队空的条件front即队头指针指向了null
链表的结构体构造要比顺序表多一些,它有两个结构体,一个是数据域,一个队列的指针域

如上图,Node结点是用来标识数据域的,而QNode是用来标识队列指针域的
入队列结点:
Queue InitQueue() //链表都需要初始化一个头结点 { Queue q; q = (Queue*)malloc(sizeof(Queue)); q->front = q->rear = NULL; return q; } void addQ(Queue Q,ElementType d){ struct Node *temp; temp=(struct Node *)malloc(sizeof(struct Node)); if(temp == NULL){ printf("未申请成功!"); return; } temp->Next=NULL; //下个结点为NULL temp->Date=d; if(Q->rear == NULL) // 新构建的结点是没有数据的,所以队头队尾都需要新增结点 { Q->front = temp; Q->rear = temp; } else{ Q->rear->Next = temp;//让n成为当前的尾部节点下一节点 Q->rear= temp;//尾部指针指向新结点 } }
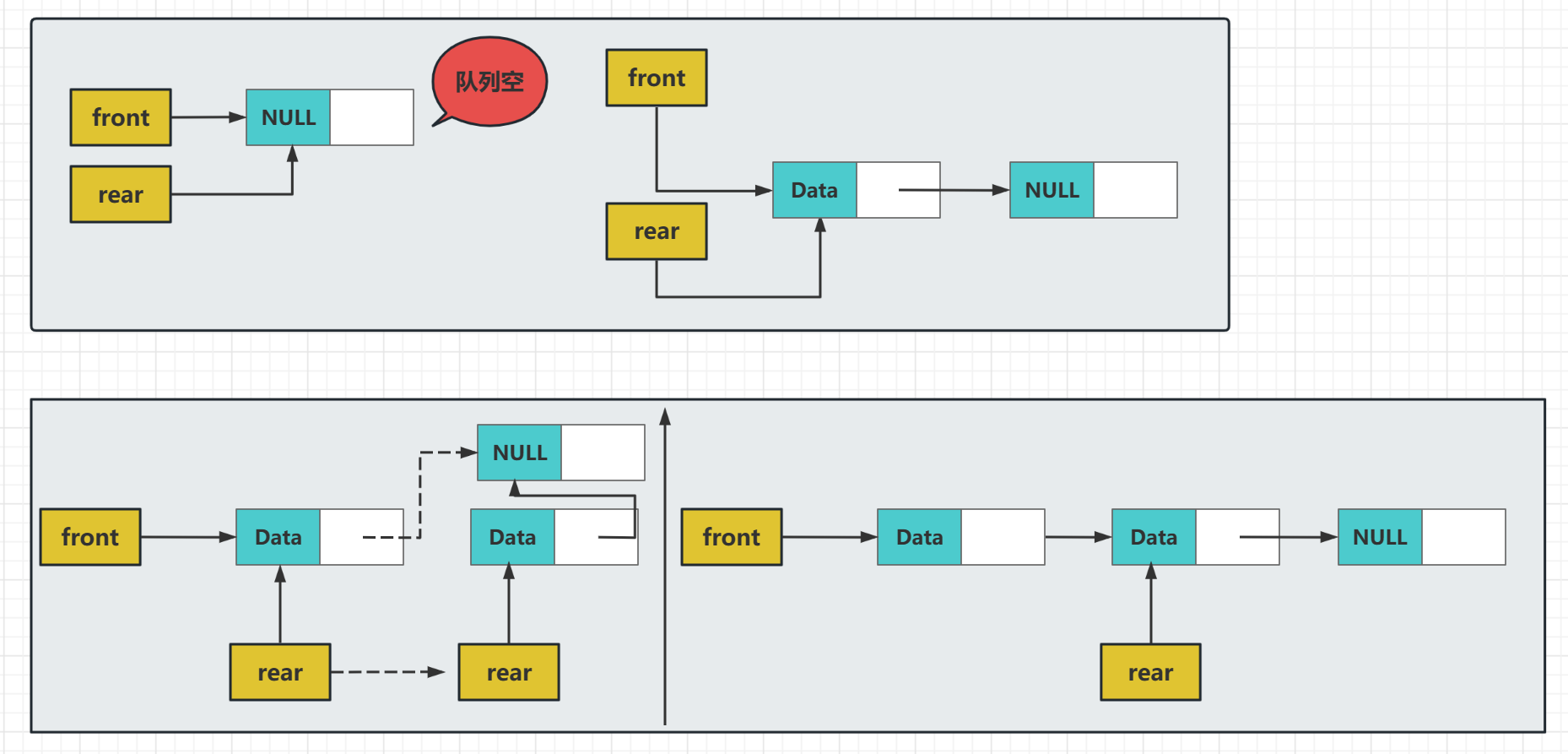
这里说一下入队列的几个注意点:
第一,队列为空的时候,它们两个指针都要指向新结点,这里可以直接指向结点不用其他操作,只是很多人会忘了头结点也要指向新结点,原因是头结点也要根据这个新结点来找到下一个结点,所以要注意
第二,然后是队列里有数据的情况,虽然不用再关注队头指针了,但是这个时候要注意队尾指针,
它是有两步操作的,它先需要把整个链表链起来,也就是当前的最后一个元素的下一个元素要是新增的结点,即 Q->rear->Next = temp;
然后就是把尾部的队列指针移动到新的结点上去,因为此时它才是尾部结点,即Q->rear= temp;
一步是关联两个结点,一步时操作队列指针,缺一不可
出队列结点:
ElementType deleteQ(Queue Q){ struct Node *temp; ElementType d; if(Q->front == NULL){ printf("队列空!"); return ERROR; } temp=Q->front; if(Q->front==Q->rear){ Q->front=Q->rear=NULL; }else{ Q->front=Q->front->Next; } d=temp->Date; free(temp); return d; }

出队列需要注意的就是:
我们要先用一个指针志昂我们要出队列的结点,然后再移动队头指针,指向下一个结点
完成指针移动后,需要把刚刚的结点空间释放掉,如果有返回值就先存放在变量里面,然后释放此结点
三.一元多项式的加法
一元多项式相加的规则(默认从大到小存储一元多项式):
当系数相等的时候:
需要对两个多项式相加,然后返回
系数不相等的时候:
返回大的多项式

这就是我们设计的多项式结构体,它包含了指数,系数,还有指向下一个多项式的指针
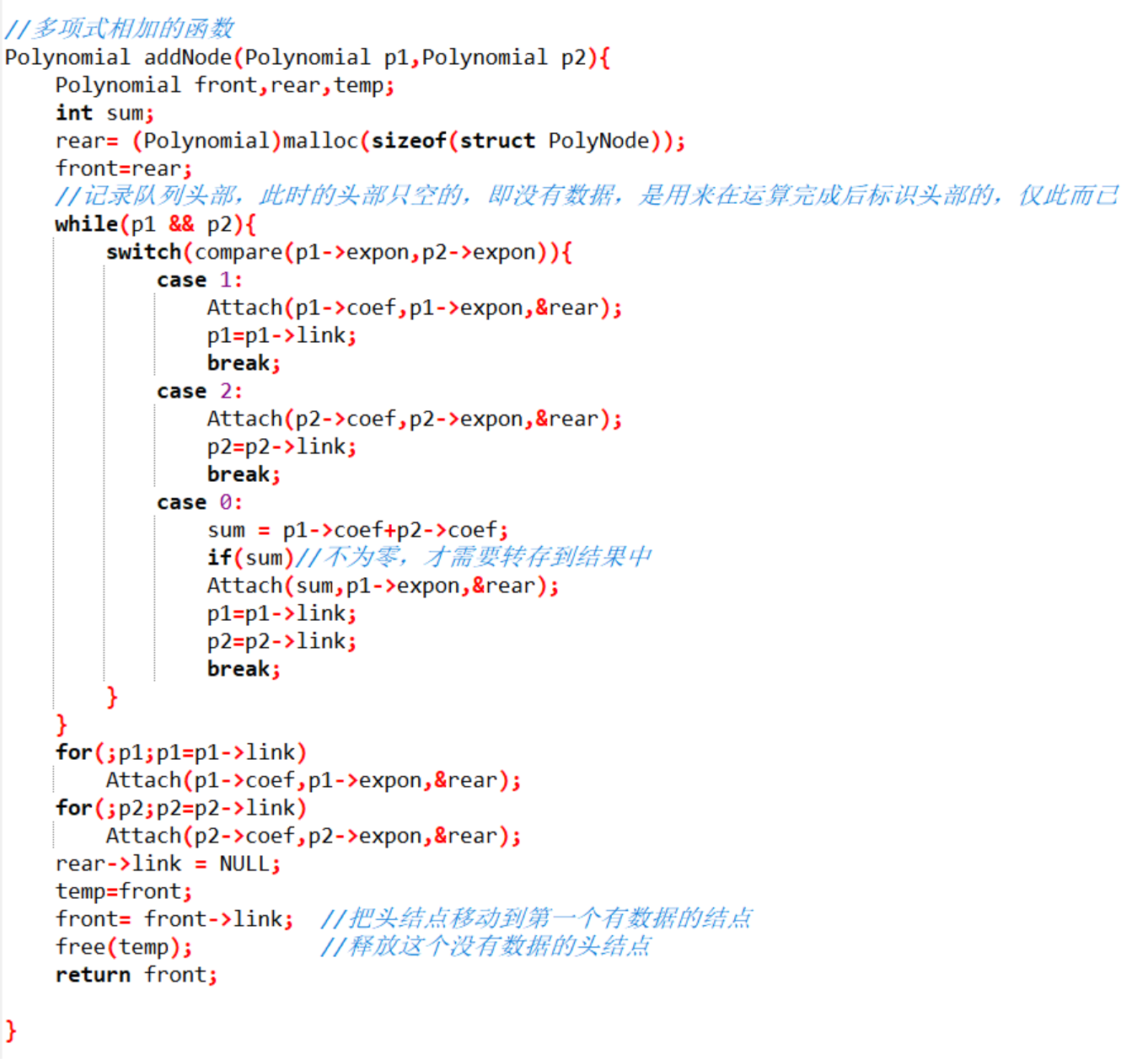
上面的代码就是我们计算多项式相加的代码,这里有几个注意点:
我们为什么要申请一个头结点,因为队列有两个指针,一个是头指针标识队列头部,一个是尾指针标识队列尾部,这里的多项式相加其实是一直入队列的过程,所以尾指针就一直移动,我们刚开始队列的两个指针是在同一位置上的,但是,一旦数据开始入队列,我们的尾指针就一直在向后移动,而我们的头指针又要指向数据,所以一共有两种方式来解决头指针不移动,且指向第一个元素的问题
第一,初始化两个指针,让它们都等于NULL,然后每次新增结点时判断头指针是否为空,如果为空,说明头指针还没指向第一个数据结点,这下可以指向它,然后下次指向新增结点的时候,就不再动头结点,而尾指针肯定是一直在移动的
第二,新增一个结点,初始头尾指针都指向它,然后再计算的时候就不带头指针了,新增结点本来都是尾指针的工作,所以可以少很多判断
我们使用的是第二种方式,这也是为什么最后我们要释放当前头结点的原因,因为这个结点是没有数据的,是空结点,我们返回值要从有数据的结点开始,所以头指针要后移一个结点,然后释放当前结点

这是我们用来循环构造一元多项式的函数
和链表入队没有什么太大的区别都是通过不断地产生新的结点,然后添加到链表的尾部,从而构成一个链队列
最后的完整代码展示:
#include<stdio.h> struct PolyNode{ int coef; //系数 int expon; //指数 struct PolyNode *link; //指向下一个结点的指针 }; typedef struct PolyNode *Polynomial; Polynomial p1,p2; // 两个待相加的多项式 int compare(int a,int b){ if(a>b) return 1; else if(a<b) return -1; else return 0; } //多项式相加的函数 Polynomial addNode(Polynomial p1,Polynomial p2){ Polynomial front,rear,temp; int sum; rear= (Polynomial)malloc(sizeof(struct PolyNode)); front=rear; //记录队列头部,此时的头部只空的,即没有数据,是用来在运算完成后标识头部的,仅此而已 while(p1 && p2){ switch(compare(p1->expon,p2->expon)){ case 1: Attach(p1->coef,p1->expon,&rear); p1=p1->link; break; case -1: Attach(p2->coef,p2->expon,&rear); p2=p2->link; break; case 0: sum = p1->coef+p2->coef; if(sum)//不为零,才需要转存到结果中 Attach(sum,p1->expon,&rear); p1=p1->link; p2=p2->link; break; } } for(;p1;p1=p1->link) Attach(p1->coef,p1->expon,&rear); for(;p2;p2=p2->link) Attach(p2->coef,p2->expon,&rear); rear->link = NULL; temp=front; front= front->link; //把头结点移动到第一个有数据的结点 free(temp); //释放这个没有数据的头结点 return front; } // 数据生成队列链表的函数 void Attach(int c,int e,Polynomial *pr){ Polynomial p; p=(Polynomial)malloc(sizeof(struct PolyNode)); p->coef=c; p->expon=e; p->link=NULL; (*pr)->link=p; *pr=p; } // 实际读入的一元多项式的函数 Polynomial ReadPoly(){ Polynomial p,rear,t; int c,e,n; printf("请输入,一元多项式的个数!\n"); scanf("%d",&n); p=(Polynomial)malloc(sizeof(struct PolyNode)); if(p==NULL){ printf("error\n"); return; } p->link=NULL; rear=p; printf("请从指数大到小输入多项式:\n"); printf("模板:系数 指数\n"); while(n--){ scanf("%d %d",&c,&e); Attach(c,e,&rear); } t=p; p=p->link; free(t); return p; } // 一元多项式的输出函数 void PrintPoly(Polynomial p){ int flag=0; if(!p){ printf("0 0\n"); return; } while(p){ if(!flag) flag=1; else printf("+"); printf("%dx^%d",p->coef,p->expon); p=p->link; } } int main(){ Polynomial p1; Polynomial p2; Polynomial p3; p1=ReadPoly(); p2=ReadPoly(); p3=addNode(p1,p2); PrintPoly(p3); }
补充:二级指针
所谓二级指针,它的作用是存放一级指针的值
我们的普通变量的值可以被一级地址指向
一级指针它也有它自己的地址,它又不是个鬼,它的地址就会被一级地址指向
只不过一级地址在初始情况下,没有指向变量的时候它的地址是一个不可访问的空间,但是它自己还是有属于自己的地址,只是指向的地址是不可访问的初始化地址
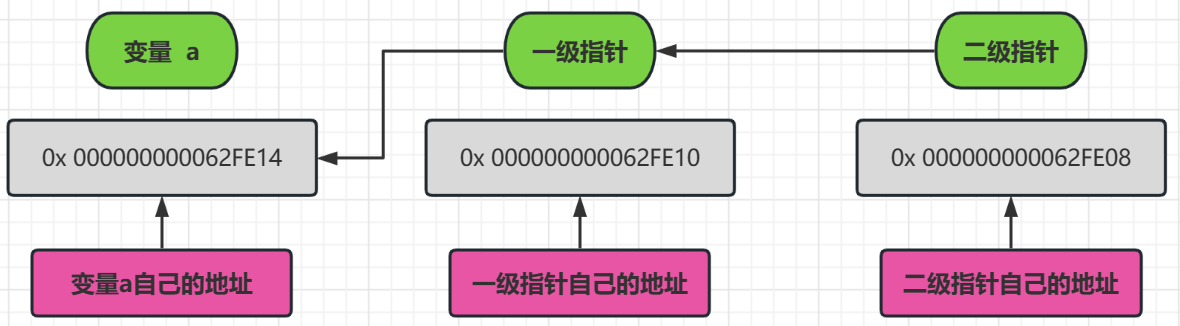
我们可以看到,指针的内部都是地址,但是操作起来可能就不一样了
也就是当 * 号操作符操作到一级指针的时候,取得的是变量 a 的值,一个具体的类型变量
当一个 * 号操作符操作到二级指针的时候,取得的是变量 一级指针的地址,也就是 a 的地址
当两个 * 号操作符操作到二级指针的时候,取得的就是 变量 a 的值,一个具体的类型变量
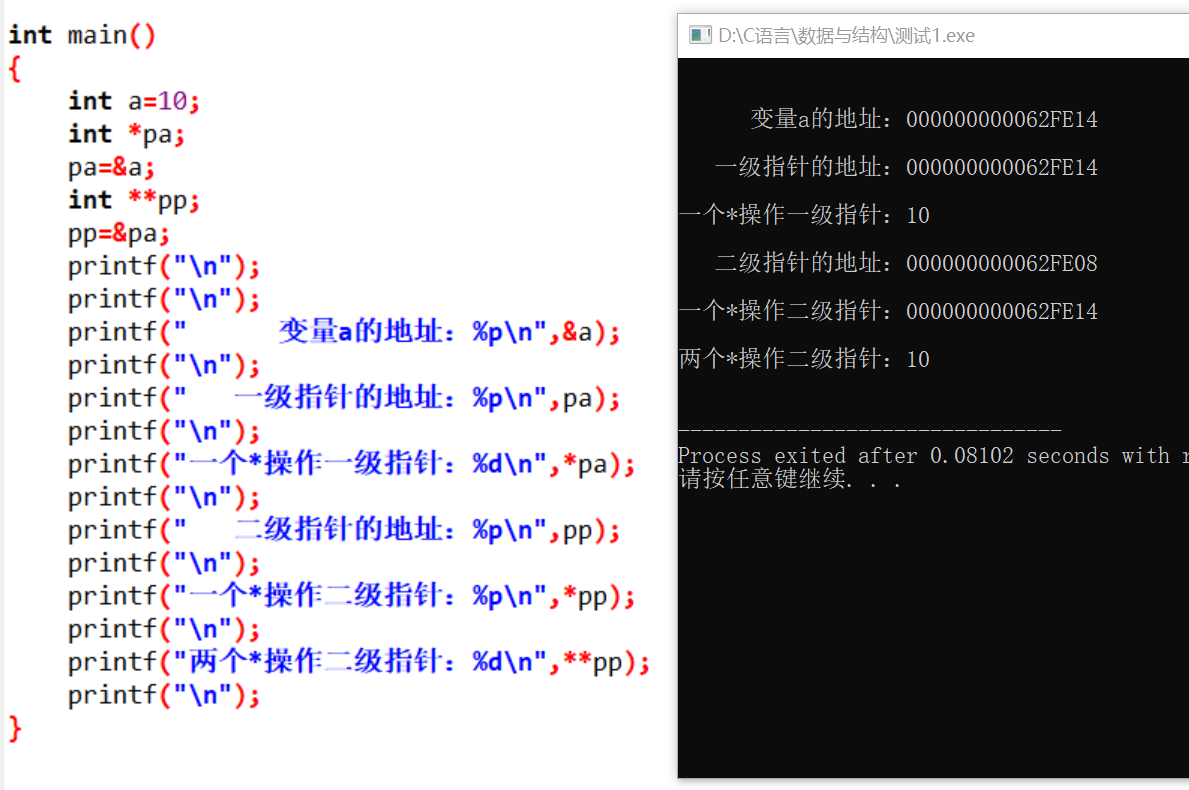
大家也可以自己去敲敲命令看看,通过观察就可以发现二级地址和一级地址在概念上应该是大差不差的
在函数的参数传递的时候,我们就会发现会使用到二级指针,因为那个函数可能要对链队列的最后一个元素操作,你要是直接传入一个指针进去,它不知道整个链队列的队尾在哪
所以你可以直接把队尾的地址传进去,直接在当前的地址后面新增结点

