导言：

我们在前面的学习中认识到了栈还有队列这些线性的数据存储结构，而现在我们要了解的数据结构却不是线性的了，我们试想线性的结构最大的缺点查询不方便，不管你是从前往后开始查找数据，还是从后往前开始查找数据都是一个一个的比对，

效率很低，所以不推荐使用，那么我们的树结构来存储的话，查找数据会不会被优化呢？

一.树的概念

什么是树？

 从更广义的角度上来说，树状结构（Tree structure），又可称为树形结构，或称树状图，其是一种将层次结构式的构造性质，以图象方式表现出来的方法。

以树的象征来表现出构造之间的关系，不过在图象的呈现上，它是一个上下颠倒的树，其根部在上方，是内容的开头，而下方的内容称为枝干与叶子。

•  树中有一个被称为根的特殊结点（根Root）
• 其余的结点互不相交集合，且本身又是一个树

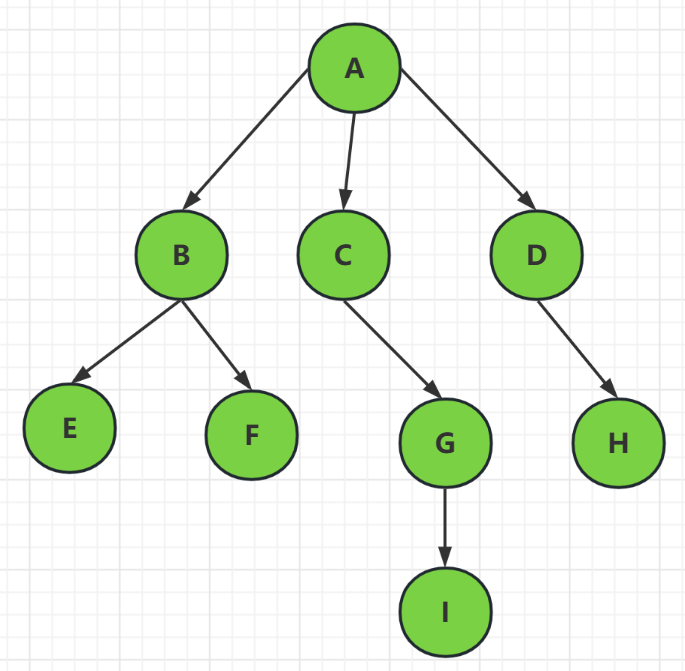
 我么现在定义的树都是无相交集合的，也就是在各个子节点之间是无法直接相连的，而且一个子节点无法同时被两个父节点指向，但是后面会有图等数据结构它又是可以的，注意区分

树的一些基本术语：

 结点的度：结点的子树的个数

如：A结点的度为3，D结点的度为1

树的度：树的结点中最大的度数

如：上面的树结点最大的度是A的3，所以树的度为3

叶节点：度为0的结点

如：结点E,FI,H都是度为0的结点

父结点：如果此结点向下一层可以找的结点，那么此结点即为下一层结点的父结点

如：结点G相对于结点I，结点G为它的上一层，所以G是I的父节点

子结点：如果此节点向上一层可以找的结点，那么对于上一层的结点，自己为子节点，也称自己为孩子结点

如：结点G相对于结点C，结点G为子结点

 兄弟结点：有同一父结点的子节点互称兄弟结点

如：结点E,F相对于结点B都是它的子结点，所以结点E,F互称兄弟结点

路径与路径长度：路径是一个结点到另一个结点所经过的结点序列，它是节点的集合，而路径长度指的是结点到结点边的个数，是边的集合

如：结点A到结点I，它的路径也就是结点序列是： {  A，C，G，I  } 即为4 ， 它的路径长度也就是边的个数是： { A -> C  ,  C -> G  ,  G -> I  }即为3

结点的层次：规定根结点在 1 层，其它任意结点的层数是其父结点的层数加 1

如：结点 G的层数是：根节点 A （1）+父节点 C（1）+ 1 即为第 3 层

树的深度：树中的所有结点的最大层次就是树的深度

如：此树的最大深度就是 A  ->  I 为  4  层 

 树的表示：

我们常用的表示方法是：儿子-兄弟表示方法

 它的实现方式是靠每个结点使用两个指针域来标识结点，一个标识的是最左边的孩子结点，一个是标识自己同层次的兄弟结点，事实证明它的空间浪费是最小的，所以使用最多

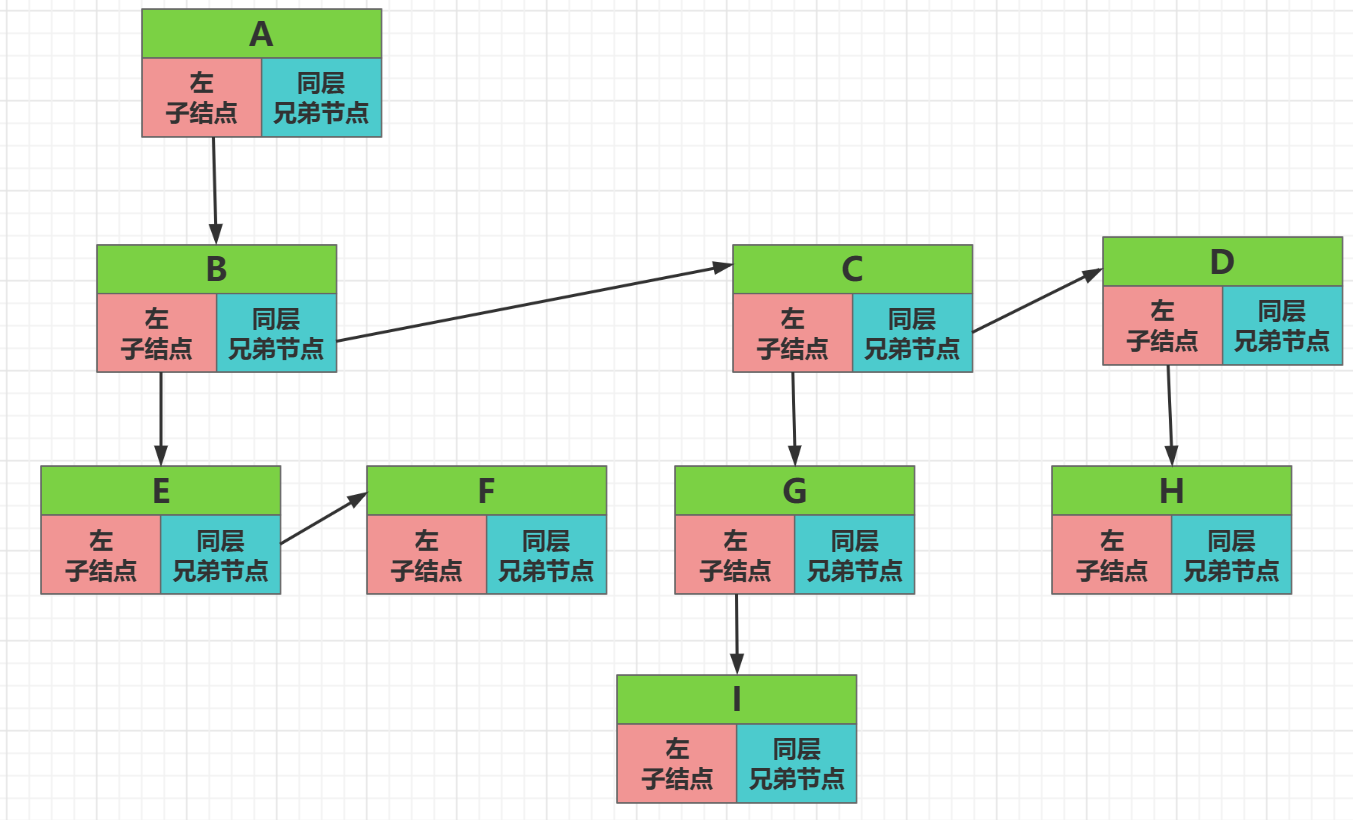
 这就是使用儿子-兄弟结点实现的上面的那一棵树

二.特别树结构之二叉树

什么是二叉树？

二叉树是n(n>=0)个结点的有限集合，该集合或者为空集（称为空二叉树），或者由一个根结点和两棵互不相交的、分别称为根结点的左子树和右子树组成。

二叉树的关键是，如果树存在，那么一定是父结点只有左子结点和右子结点两个结点，并且两个结点可以独立存在，不一定要成对出现它的子结点区间一定是  0 <= n  <=2

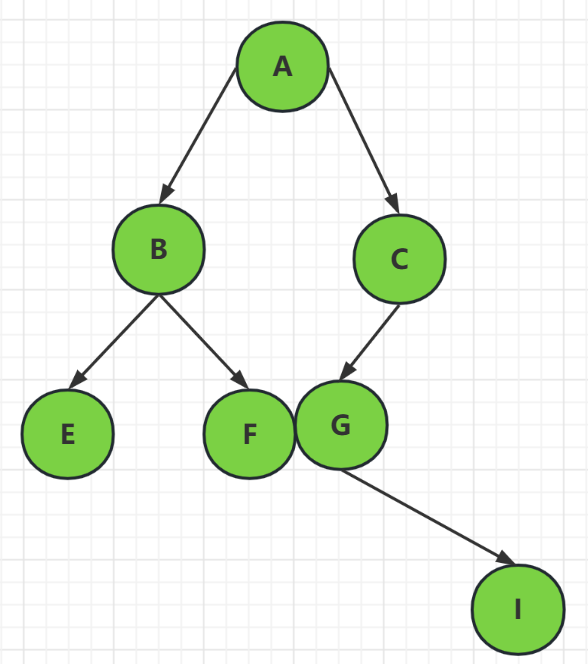
 上面的就是一棵很正常的二叉树

在二叉树存在的情况下，我们有的父结点右两个结点，有的只有一个结点，有的没有结点被称为叶子结点

我们来看看几种特殊的二叉树：

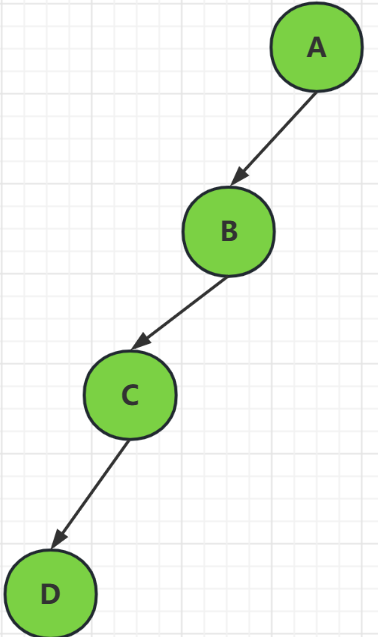
 这种叫斜二叉树，它的结点都向一边倾斜

图中的是往左子结点倾斜，其实全部往右倾斜也是一样的，都是斜二叉树，它的结构就和线性结构差不多了，跟链表也差不多

但是它们都是二叉树的一种结构，也是符合二叉书的特点的

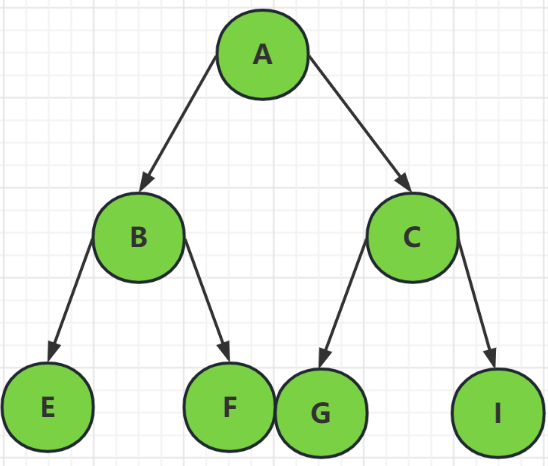
 这种是满二叉树，也是很完美的二叉树，

它的子结点都是均匀分布在左右的，而且空间浪费是二叉树中最少的

后面的学习多向满二叉树发展

二叉树的顺序存储：

由于二叉树的规律很明显，即树存在时，一个父结点只有最多有两个结点

且我们的完全二叉树是最适合利用数组来存储的，它的结构特特征很符合数组，并且可以很快的找到父结点和子结点

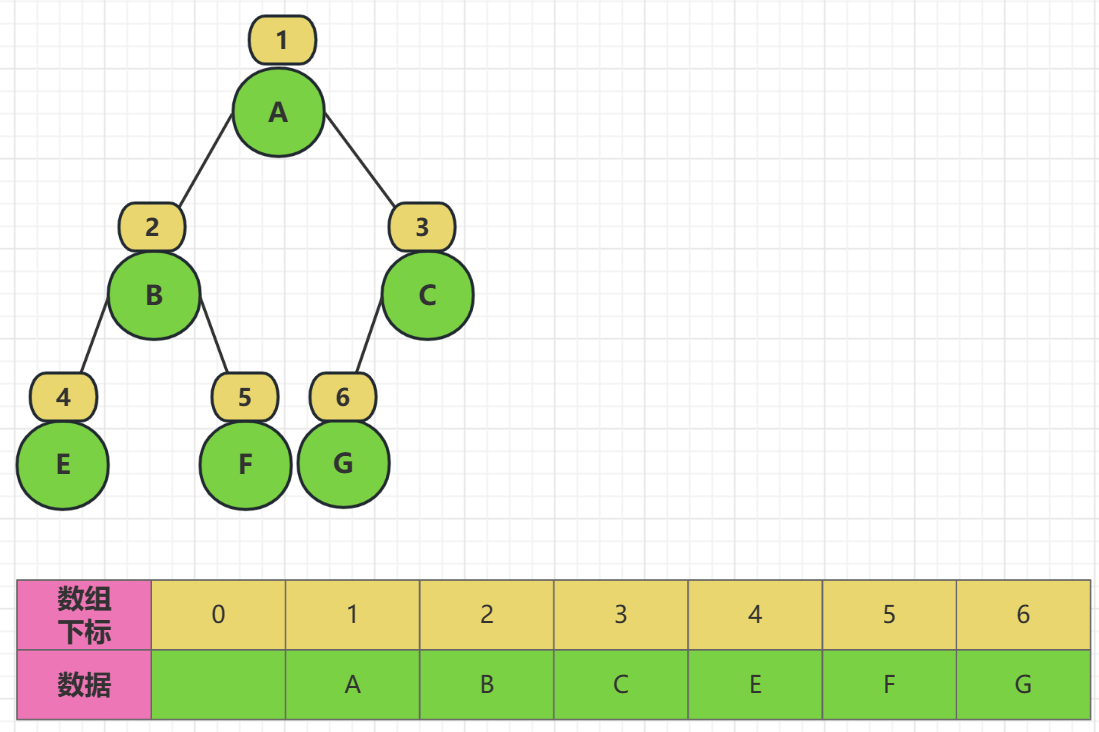
 从上面的图中我们可以很快的推算出子结点和父结点的位置

父结点：当前结点 / 2（取整）

子结点：左子节点，当前结点 *2 ，右子结点，当前结点 *2 + 1 ，计算的结果要小于 n  （结点的个数），否则无子结点

此外，我们还有一些非完全二叉树，对于它们使用数组来存储的话需要利用null值来补满成完全二叉树，但是会有空间浪费

 二叉树的链表实现：

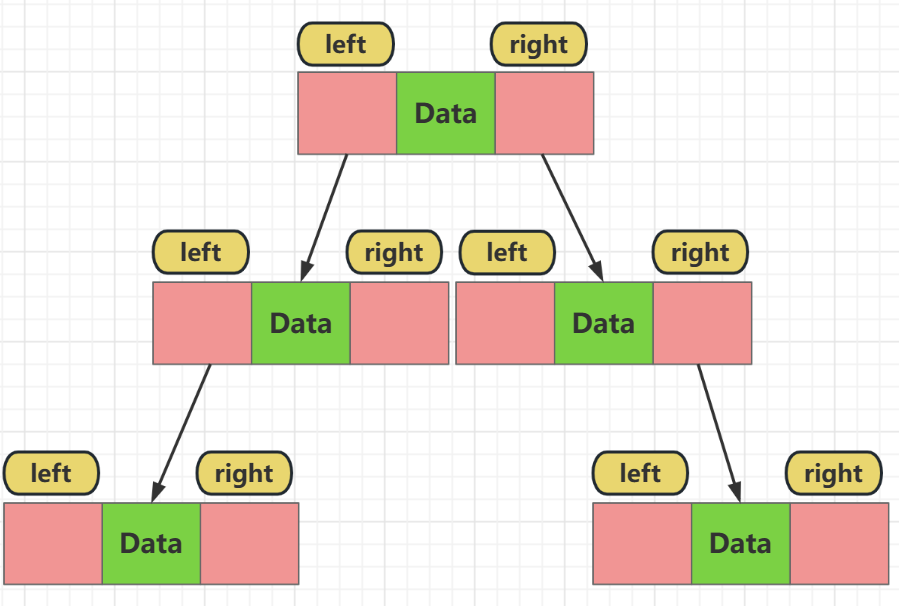
typedef int ElementType;
typedef struct TreeNode* BinTree;
typedef BinTree Position;
struct TreeNode
{
    ElementType Data;
    BinTree Left;
    BinTree Right;
};

上面是二叉顺结点的结构

 三.二叉树的遍历

 二叉树的先序遍历：

遍历过程为：

1. 先访问根结点
2. 先序遍历左子树
3. 先序遍历右子树

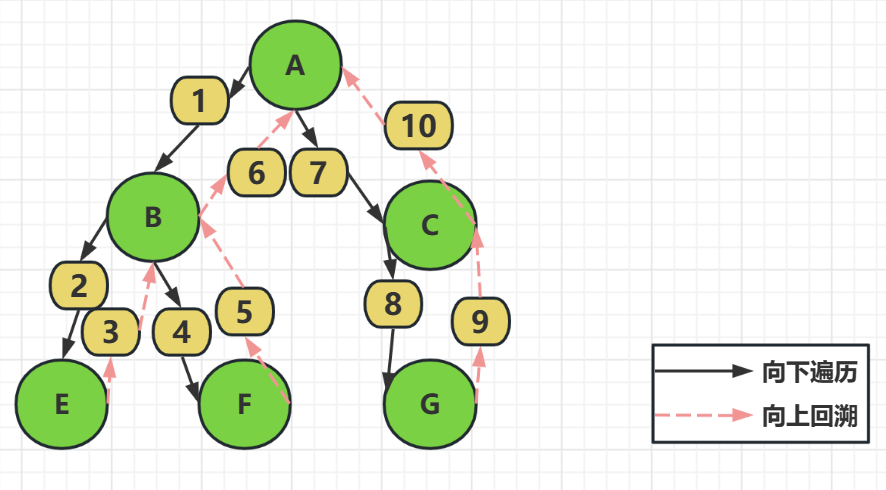
 先序遍历部分的代码（递归实现）：

void PreOrderTraversal(TreeNode *BT){
    if(BT){ //结点存在 
        printf("%d",BT->Data);
        PreOrderTraversal(BT->Left);
        PreOrderTraversal(BT->Right);
    }
}

先序遍历的结果是：A , B , E , F , C ,  G

二叉树的中序遍历：

遍历过程为：

1. 中序遍历其左子树
2. 访问根节点
3. 中序遍历其右子树

 中序遍历部分代码实现（递归）：

void PreOrderTraversal(TreeNode *BT){
    if(BT){ //结点存在 
        PreOrderTraversal(BT->Left);
        printf("%d",BT->Data);
        PreOrderTraversal(BT->Right);
    }
}

中序遍历的结果是：

E , B , F ,  A  ,  C  ,  G

二叉树的后序遍历：

遍历过程为：

1. 后序遍历其左子树
2. 后序遍历其右子树
3. 访问根结点

 后序遍历部分代码实现（递归）：

void PreOrderTraversal(TreeNode *BT){
    if(BT){ //结点存在 
        PreOrderTraversal(BT->Left);
        PreOrderTraversal(BT->Right);
        printf("%d",BT->Data);
    }
}

后序遍历的结果：

E  ,  F  ,  B  ,   G  ,  C  ,  A

总结：

其实三种遍历方式都是对根结点位置的描述，然后遵循先左子树后右子树的特点

先序遍历：根节点，左子树，右子树

中序遍历：左子树，根节点，右子树

后序遍历：左子树，右子树，根节点

中序非递归遍历：

中序的非递归遍历使用的是循环的思想，然后使用堆栈作为数据存储结构

我们根据中序遍历的思路，它是先遍历了左子树，然后访问根节点，遍历右子树

所以说我们可以先让根结点入栈，然后一直让左子树的左结点入栈，直到当前的结点没有左节点时，把指针转向它的它的右节点，然后出栈左结点和它的父结点

我们再使用同样的方法入栈当前的右节点的左节点，如果没有左节点就出栈，没有此结点就下一次循环了

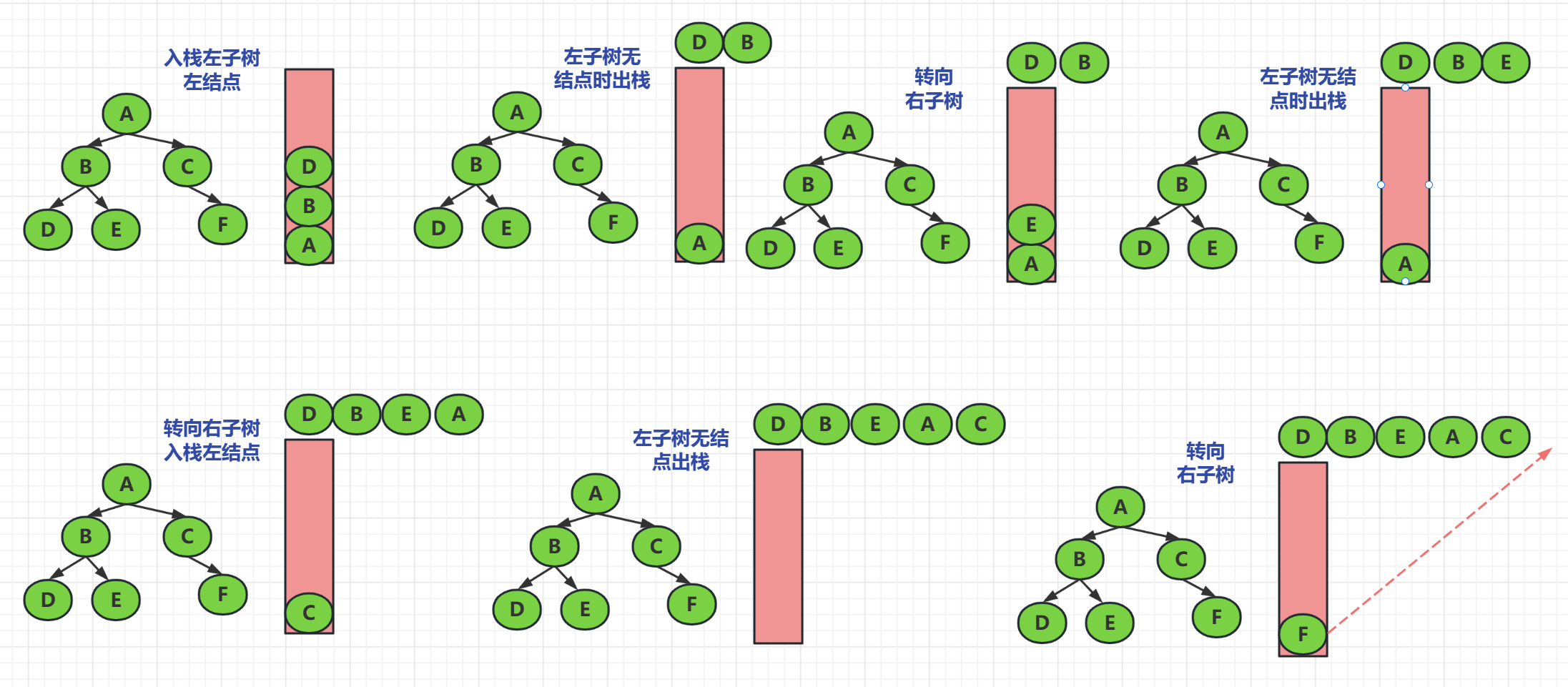
 上面是图片解析我们的中序非递归遍历

然后是代码实现：

void InOrderTraversal(TreeNode *BT){
    TreeNode *T=BT;
    Stack s = CreateStack(Maxsize);
    //开辟一个数组栈空间 
    While(T || !IsEmpty(s)){
        // 树结点不为空，并且栈内还有元素 
        while(T){
            //树结点存在 
            push(s,T);
            T=T->Left;
        }
        if(!isEmpty(s)){
            //栈不为空 
            T=pop(s); 
            printf("%d\n",T->Data);
            T=T->Right;
        }
    }
}

中序遍历也可以改为先序遍历，只需要把输出函数放在，入栈函数push（）后面即可

层序遍历：

层序遍历的思想是使用队列加循环完成的，它和后面要学习的图的遍历很像

由于队列的特点是先进先出，所以它的遍历是一层一层向下进行的

队列实现：遍历从根结点开始，首先将根结点入队，然后开始执行循环：结点出队，访问此结点，入队它的孩子结点

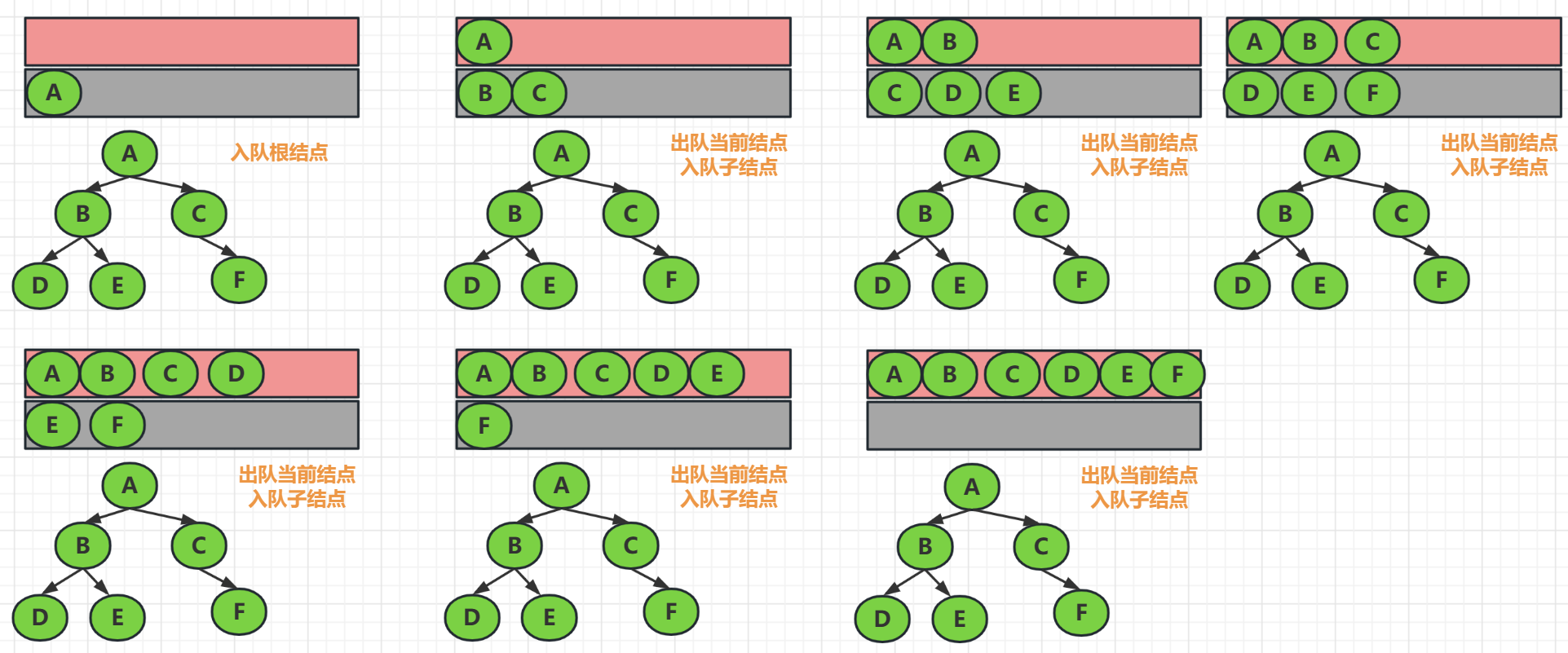
 使用队列来遍历二叉树，很显然它是一层一层的输出结果的

然后代码实现：

void LevelOrderTraversal(TreeNode *BT){
    Queue Q;
    TreeNode *T;
    if(!BT)
    //空树直接返回 
    return;
    Q = CreateQueue(Maxsize);
    //创建一个队列 
    AddQ(Q,BT);
    //把根结点先入队
    while(!isEmptyQ(Q)){
        T = Delete(Q); 
        printf("%d\n",T->Data);
        //出队结点 
        if(T->Left)
        AddQ(Q,T->Left);
        //入队左子结点 
        if(T->Right)
        AddQ(Q,T->Right);
        //入队右子结点 
    }
}

已知两个遍历序列，来求二叉树

已知先序序列：a，b，c ，d，e，f，g，h，i，j

已知中序序列：c，b，e，d，a，h，g，i，j，f

首先我们要根据先序序列，推出我们的根结点为a，那么再中序序列中，a左边的就是左子树，右边的就是右子树

 然后根据中序序列也可以把先序学列划分成左子树和右子树，根据长度划分，左子树b，c ，d，e，右子树f，g，h，i，j，然后各个子树的第一个元素又是当前子树的根结点，又可以再已划分的中序序列中去继续找左子树和右子树

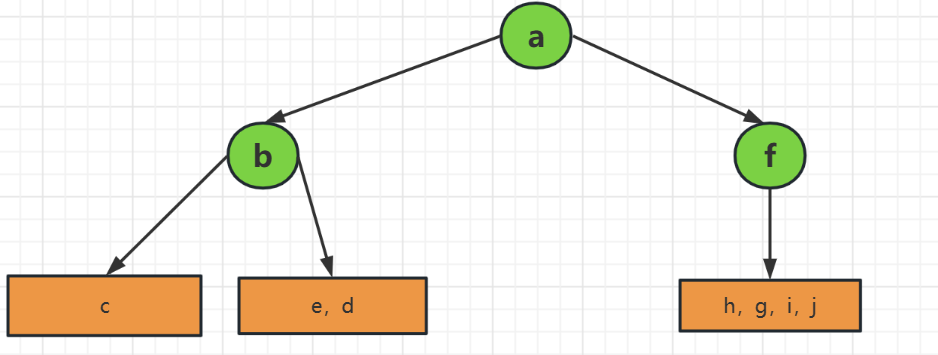
 我们看到左子树，在先序序列中找到e元素和d元素，先序序列中它的顺序是d，e，那么第一个元素就是根结点即d为根结点，e为子结点，有根据中序序列的e，d，说明先访问子结点，那么e一定是左子结点

右边，先序序列是g，h，i，j，说明g是下一层的根结点，由于中序序列它们的父结点是后访问，说明g，h，i，j都位于左子结点，

 我们可以看到，左子树已经推算完了，然后就是右子树，

肯定是一个相对于g的左子结点，主要是i，j，我们看看先序序列也是i，j，说明i是根节点，由于中序遍历的i，j说明先访问根结点，那么j一定是i的右子结点

 这样一棵二叉树就被我们给推算出来了