1. 引入Markov Model
• 定义
如果一个系统存在n个状态S1,S2,S3,...Sn,随时间推移,该系统从某一状态转移到另一状态。用qt表示系统在时间t的状态变量,那么t时刻的状态取值为Sj的概率取决于前t-1个时刻的状态,该概率为
![]()
– 假设1:如果在特定情况下,系统在时间 t 的状态只与其在时间 t-1 的状态相关,则该系统构成一个离散的一阶马尔可夫链
– 假设2:如果只考虑独立于时间 t 的随机过程,状态与时间无关,即t时刻状态的概率取决于前 t-1 个时刻(1, 2, …, t-1)的状态,且状态的转换与时间无关,则该随机过程就是马尔可夫模型
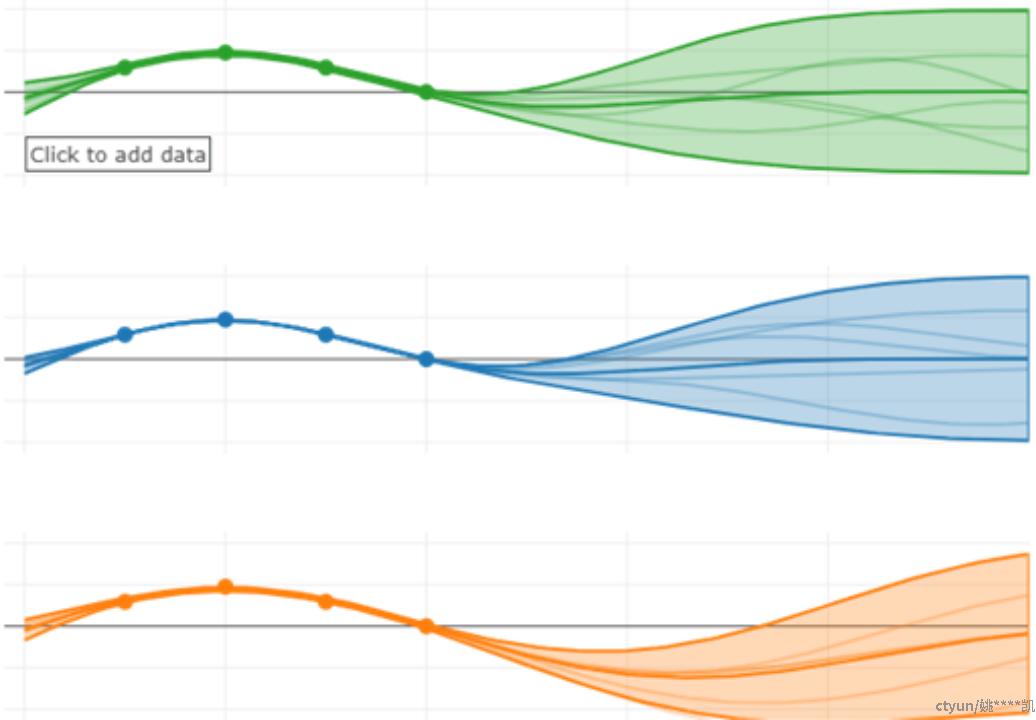
2. HMM基本阐释
• 概念导入
在马尔可夫模型中,每个状态代表了一个可观察的事件,所以,马尔可夫模型有时又称作可视马尔可夫模型(Visible Markov Model,VMM),这在某种程度上限制了模型的适应性。
对于盲人来说也许不能够直接获取到天气的观察情况,但是他可以通过触摸树叶通过树叶的干燥程度判断天气的状态。于是天气就是一个隐藏的状态,树叶的干燥程度是一个可观察的状态,于是我们就有了两组状态,一个是不可观察、隐藏的状态(天气),一个是可观察的状态(树叶),我们希望设计一种算法,在不能够直接观察天气的情况下,通过树叶和马尔可夫假设来预测天气。
• 概念
在隐马尔可夫模型(HMM)中,我们不知道模型具体的状态序列,只知道状态转移的概率,即模型的状态转换过程是不可观察的。
HIDDEN STATES: Rainy and Sunny
OBSERVATIONS: Walk, Shop and Clean
NOTE:在机器学习中, 观测序列为训练数据, 状态值为数据的标注,也是模型输出的值
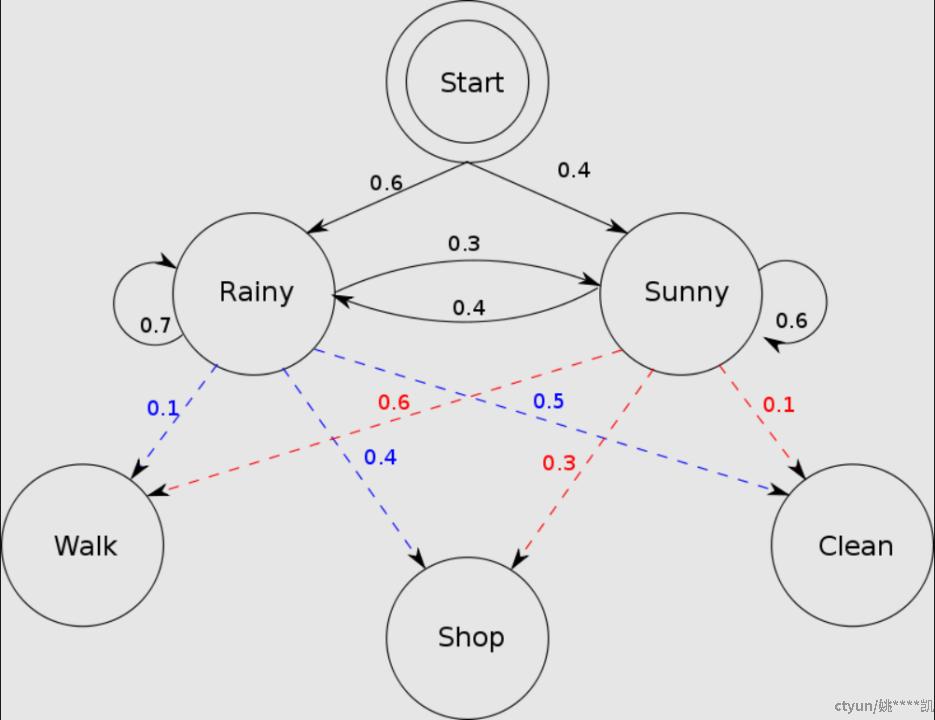
因此,该模型是一个双重随机过程,包括模型的状态转换和特定状态下可观察事件的随机。
• 如何理解?
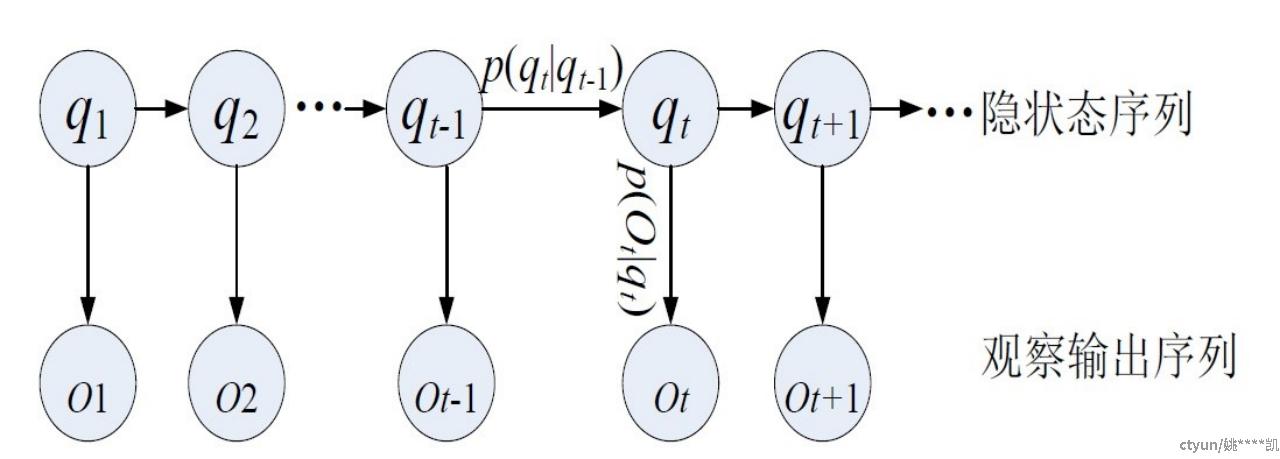
状态序列为:q1,q2,...,qn
观测序列为:O1,O2,...,On
问题转化为:已知输入序列O1,O2,...,On,对应的最可能的中文字q1,q2,...,qn。求最可能的汉字序列?
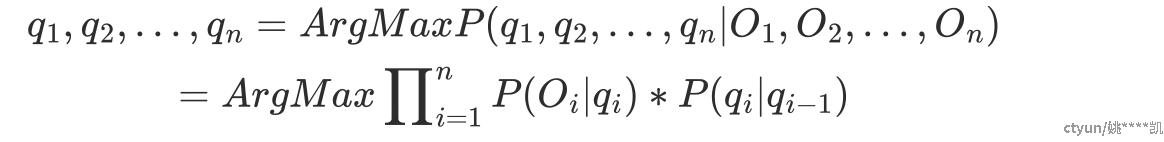
从众多状态值序列中找到一组使得联合概率(包括观察序列的概率)最大的路径q1,q2,...,qn
3. HMM的训练过程
本节以==中文分词==为例,进行HMM的原理阐述。假设有一个3句话组成的语料库,空格表示分词
今天 天气 真 不错
浦东新区 在 下雨
我 是 真的 喜欢 晴天
3.1 HMM的基本元素
• 5个基本元素
I 状态序列:在分词中为每个中文字的标注,即状态值,分词中的状态值有4种(BMSE),见3.2
O 观测序列:中文字本身
π 初始概率矩阵:每个标注的初始化概率,计算方法见3.3
A 状态概率转移矩阵:从一种标注转移到另一种标注的概率组成的矩阵,计算方法见3.4
B 发射概率矩阵:在每个个标注下,生成每个字的概率组成的矩阵,计算方法见3.5
==HMM的训练目标:通过语料库中的每个字和对应标记,统计计算π,A和B==
3.2 状态值集合
• BMSE标签,分别代表每个状态代表的是该字在词语中的位置,具体如下:
– B - begin ----> 该字是词语中的起始字
– M - middle -----> 词语中的中间字
– S - single -----> 表是单字成词
– E - end -----> 词语中的结束字
• Example
|
今 |
天 |
天 |
气 |
真 |
不 |
错 |
|
|
B |
E |
B |
E |
S |
B |
E |
|
|
浦 |
东 |
新 |
区 |
在 |
下 |
雨 |
|
|
B |
M |
M |
E |
S |
B |
E |
|
|
我 |
是 |
真 |
的 |
喜 |
欢 |
晴 |
天 |
|
S |
S |
B |
E |
B |
E |
B |
E |
3.3 初始概率矩阵
• 统计语料库中每句话第一个字的标记,分别得到BMES的个数
• 得到一个1*4的矩阵
• 归一化,将其变为概率
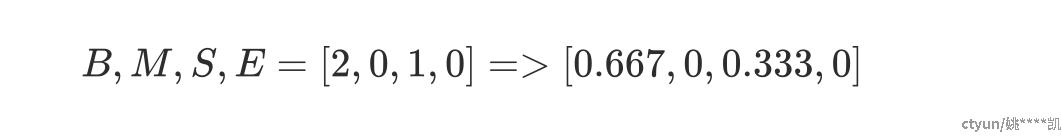
3.4 转移概率矩阵
• 分别统计某个状态到另个状态转移的频次
• 转移概率矩阵为4*4矩阵
• 由于从A状态到B状态和B状态到A状态不同,所以该矩阵是非对称的
|
|
B |
M |
S |
E |
|
|
|
B |
M |
S |
E |
|
B |
0 |
1 |
0 |
7 |
|
|
B |
0 |
0.125 |
0 |
0.875 |
|
M |
0 |
1 |
0 |
1 |
|
|
M |
0 |
0.5 |
0 |
0.5 |
|
S |
3 |
0 |
1 |
0 |
|
|
S |
0.75 |
0 |
0.25 |
0 |
|
E |
3 |
0 |
2 |
0 |
|
|
E |
0.6 |
0 |
0.4 |
0 |
3.5 发射概率矩阵
• 统计每个标签下每个字的出现频次
|
|
今 |
天 |
气 |
真 |
不 |
错 |
浦 |
东 |
新 |
区 |
在 |
下 |
雨 |
我 |
是 |
的 |
喜 |
欢 |
晴 |
|
B |
1 |
1 |
|
1 |
1 |
|
1 |
|
|
|
|
1 |
|
|
|
|
1 |
|
1 |
|
M |
|
|
|
|
|
|
|
1 |
1 |
|
|
|
|
|
|
|
|
|
|
|
S |
|
|
|
1 |
|
|
|
|
|
|
1 |
|
|
1 |
1 |
|
|
|
|
|
E |
|
2 |
1 |
|
|
1 |
|
|
|
1 |
|
|
1 |
|
|
1 |
|
1 |
|
• 行归一化得到发射概率矩阵 4*19
|
|
今 |
天 |
气 |
真 |
不 |
错 |
浦 |
东 |
新 |
区 |
在 |
下 |
雨 |
我 |
是 |
的 |
喜 |
欢 |
晴 |
|
B |
0.125 |
0.125 |
|
0.125 |
0.125 |
|
0.125 |
|
|
|
|
0.125 |
|
|
|
|
0.125 |
|
0.125 |
|
M |
|
|
|
|
|
|
|
0.5 |
0.5 |
|
|
|
|
|
|
|
|
|
|
|
S |
|
|
|
0.25 |
|
|
|
|
|
|
0.25 |
|
|
0.25 |
0.25 |
|
|
|
|
|
E |
|
0.25 |
0.125 |
|
|
0.125 |
|
|
|
0.125 |
|
|
0.125 |
|
|
0.125 |
|
0.125 |
|
4. HMM预测过程
• 给定预测句子示例:
Sentence: 真 是 喜欢 下雨
True Label: S S BE BE
• HMM的预测目标:通过训练统计出的π,A和B三个矩阵,从多条状态序列中==选出一条路径==,使得其转移和发射的联合概率最大,这里就用到了预测时给定的句子,因为在计算状态序列联合概率时要计算每个标签转移到给定句子每个字的概率
• 预测示意图
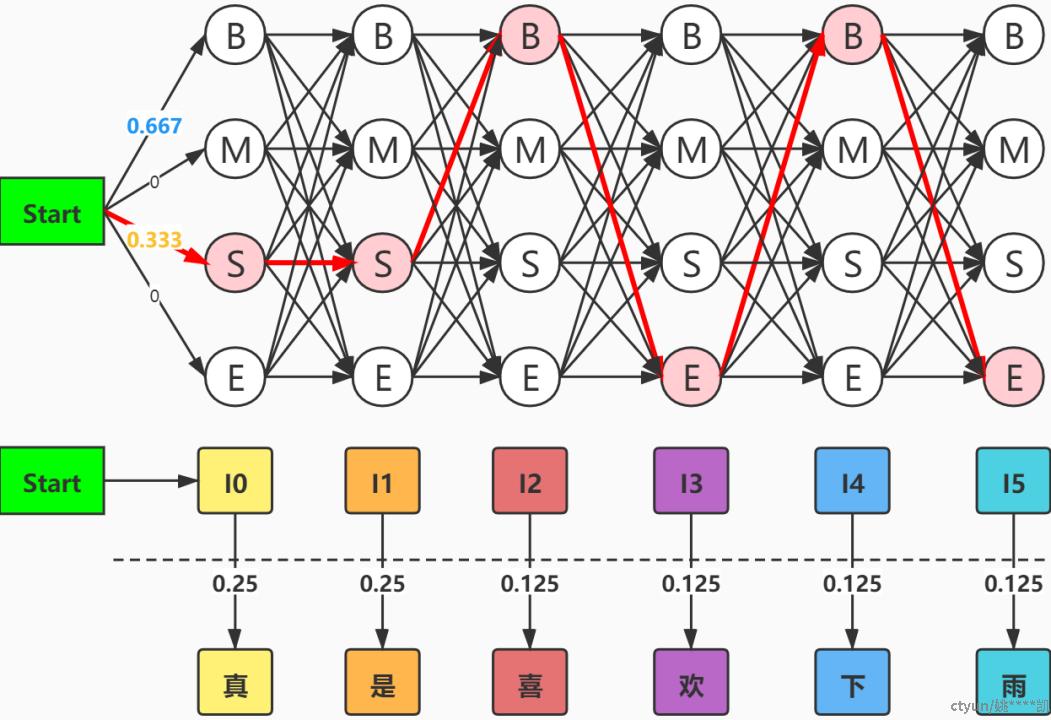
• 计算最优路径概率P
0.333 * 0.25 * ( 0.25 * 0.25 ) * ( 0.75 * 0.125 ) * ( 0.875 * 0.125 ) * ( 0.6 * 0.125) * (0.875 * 0.125)
st->S S->真 S->S S->是 S->B B->喜 B->E E->欢 E->B B->下 B->E E->雨
• 这条状态转移路径中共有 4^6 种路径,按照上面的方法计算出每条路径的联合概率,选择概率最大的那条路径 S--->S--->B--->E--->B--->E
5. Viterbi算法
5.1 为什么使用Viterbi算法
• 如果对所有路径进行枚举,对于M种状态值以及长度为N的观测序列,其理论路径数目为M^N,^对每种路径计算概率(这里可认为概率计算为常量级数),则时间复杂度为O(M^N)
• 假定状态数一定,那么其时间复杂度随着序列的长度增长而呈指数级增长,极大降低了运算效率
• 为了能在观测序列长度较大时,快速找出最优路径,采用此算法
5.2 算法过程
以上述的分词过程为例,其过程如下图所示
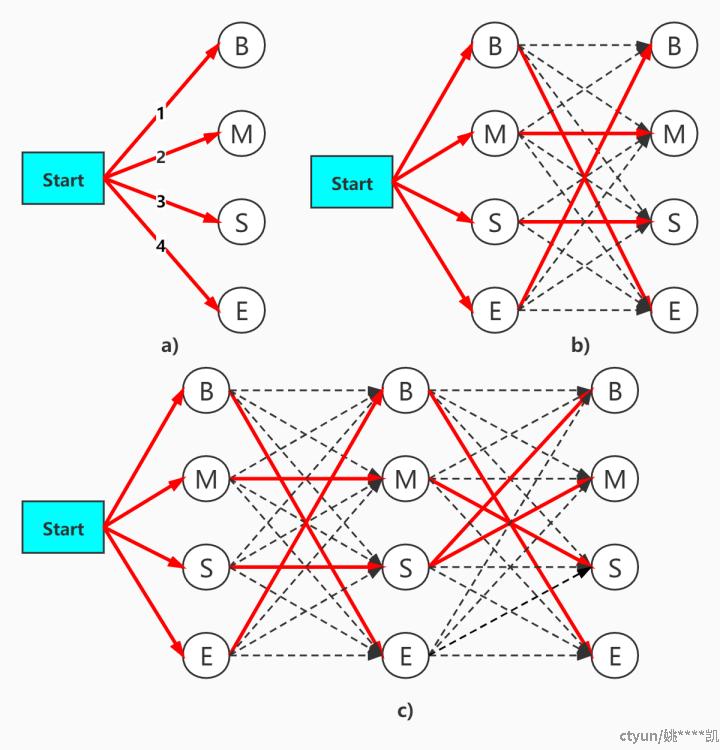
• 如上图a) 所示:对于每个状态值而言,从初始态连接的路径均只有1条,此时的初始概率只是局部最优解,因此全部保留;
• 如上图b) 所示:对于当前状态的每个值而言,从上一个状态连接过来的路径有4条,从中选取最优的一条,其余的前部删除,这样从状态I0--->I1,只保留了4条最优路径
• 如上图c) 所示:同理从l1--->l2,只保留4条最优路径
• 以此类推,可得到一个下图所示的最优路径转态转移图
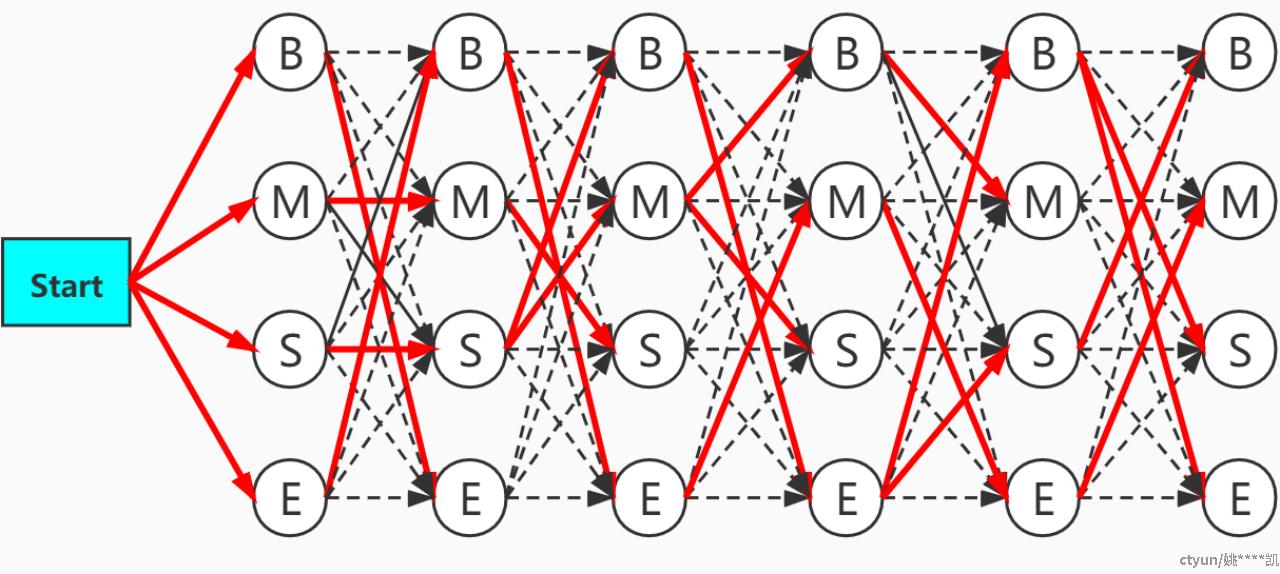
5.3 总结
• 比如在st---> I0--> I1的路径中,假设经过st-->E--->B的路径最短,那么其他3条路径 [ st-->s--->B, st--->M--->B, st--->B--->B ]绝对要比st-->E--->B的距离长,其他状态值同理
• 在每步的迭代中,总是保留最优的唯一路径,因此,使得下一步迭代的路径选择也仅有M(状态数)条
• 因此在迭代完毕后,整体的最优路径也仅有M条
• 这样,Viterbi算法将一个 α* O(M^N) 复杂度的计算降为 β * O(M*N)级,极大提升了计算效率,α和β都是常量级复杂度计算:
α:整条路径的概率计算
β:每步择优时的局部路径概率计算