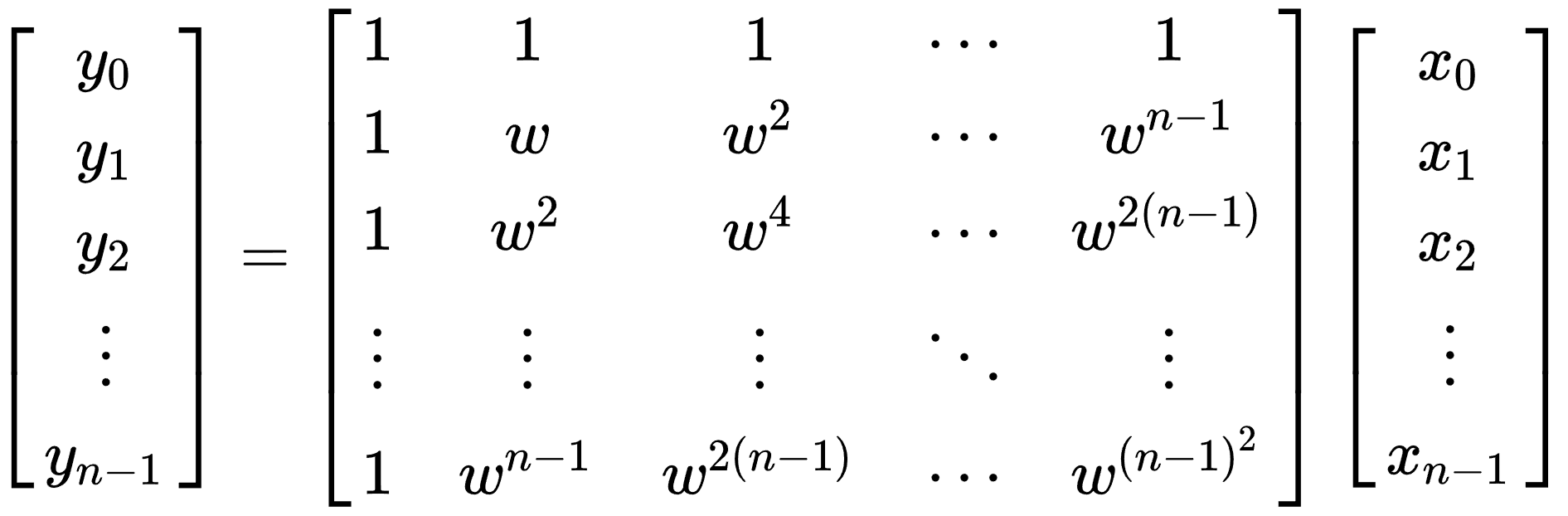1. Convolutional
-
定义
- 一维:
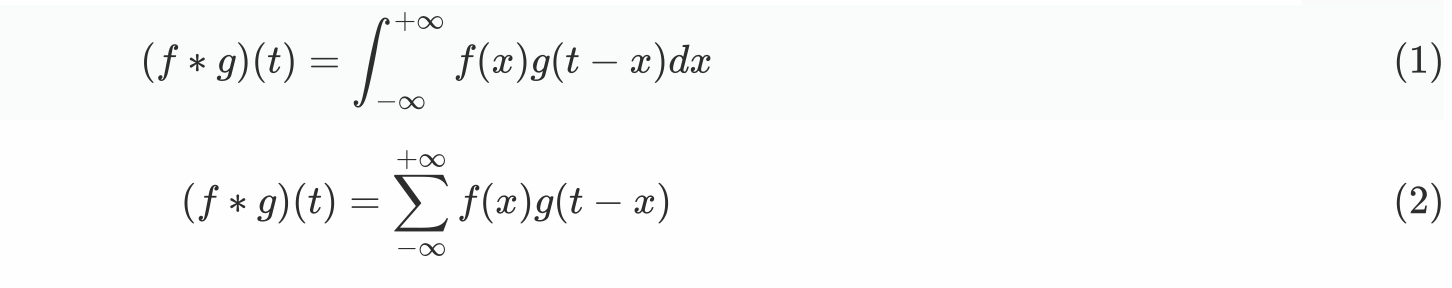
- 二维:
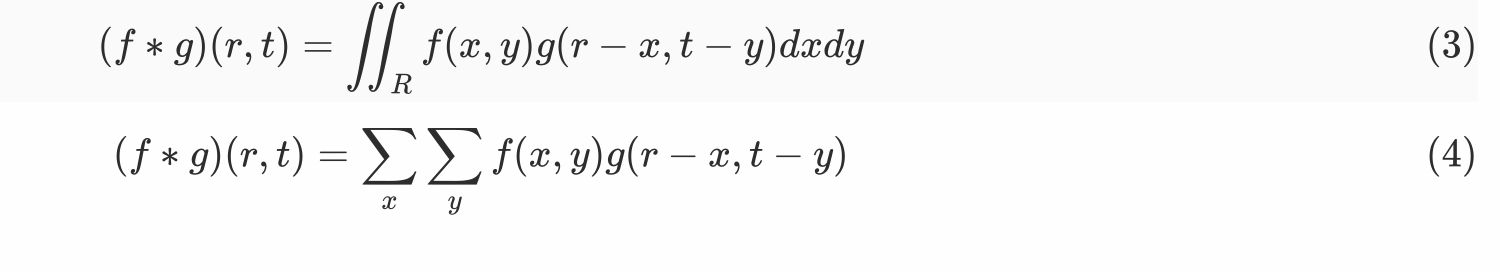
- 一维:
-
理解
- 所谓两个函数的卷积,本质上就是先将一个函数翻转,然后进行滑动叠加
- 在连续情况下,叠加指的是对两个函数的乘积求积分,在离散情况下就是加权求和,为简单起见就统一称为叠加
- **卷积的“卷”,指的的函数的翻转,从 **g(t) 变成 g(-t) 的这个过程;同时,“卷”还有滑动的意味
- 卷积的“积”,指的是积分/加权求和
-
例子
有两枚骰子,把它们都抛出去,两枚骰子点数加起来为4的概率是多少?

**两枚骰子点数加起来为4的情况有三种情况:1+3=4, 2+2=4, 3+1=4,因此,两枚骰子点数加起来为4的概率为:**

首先,因为两个骰子的点数和是4,为了满足这个约束条件,我们还是把函数 g 翻转一下,然后阴影区域上下对应的数相乘,然后累加,相当于求自变量为4的卷积值,如下图所示:
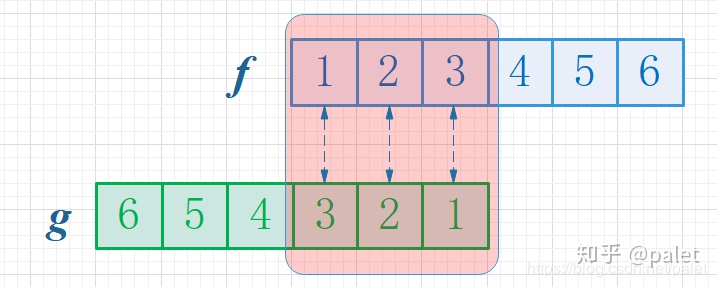
**其次,如此翻转以后,可以方便地进行推广去求两个骰子点数和为 n 时的概率,为f 和 g的卷积 f*g(n),如下图所示:

**由上图可以看到,函数 **g 的滑动,带来的是点数和的增大。此例子中对f和g的约束条件就是点数和,它也是卷积函数的自变量。
2. Fourier Transform
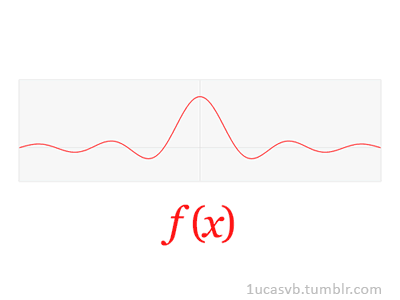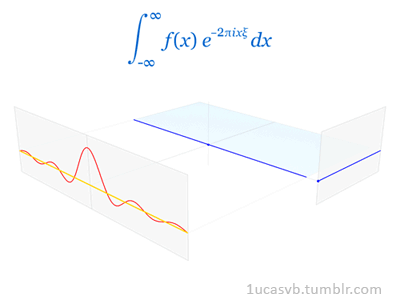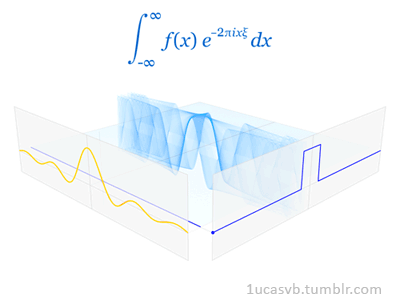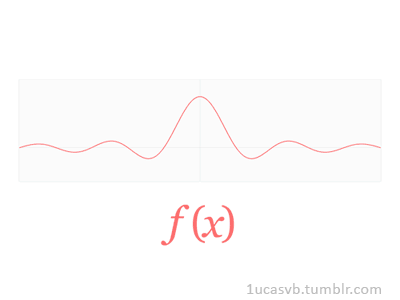
- Fourier变换和逆变换定义
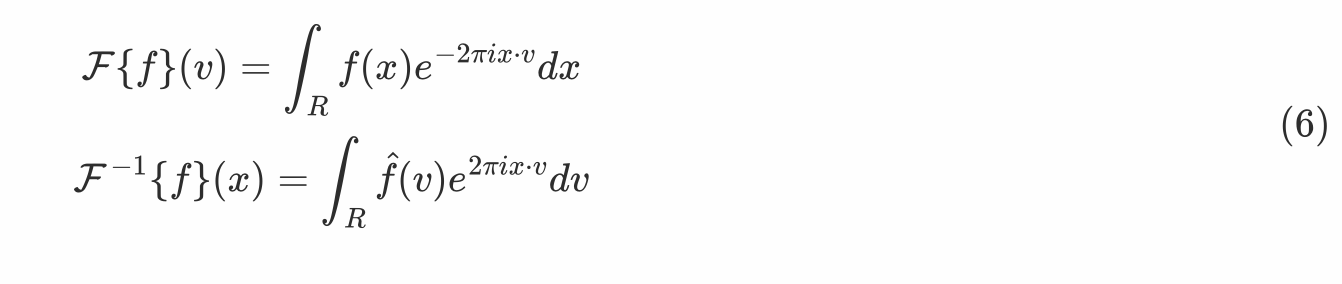
- 卷积定理
函数卷积的傅里叶变换是函数傅里叶变换的乘积

- 由卷积定理可将卷积公式写作如下

- 理解
**函数f(x)可以想象成一个长度为无穷的向量,==函数空间中的内积定义为积分==。上面傅里叶变换的公式中,将 e^-2pixv 看做基,则整个式子就是在算f(t)在这个基上的坐标,所有的v都算一次,就可以得到f(t)在这组基上的完整坐标,这就是F{f}(t)这个函数的含义。**
==****而这个基,恰好是拉普拉斯算子的特征向量。==
3. Laplacian Matrix
3.1 定义
拉普拉斯算子是 n 维欧几里得空间中的一个二阶微分算子,其定义为对函数 f 先作梯度运算后,再作散度运算的结果

在笛卡尔坐标系中的所有非混合二阶偏导数之和

3.2 图上的Laplacian算子
** 图拉普拉斯矩阵,如果把它看作线性变换的话,它起的作用与数学分析中的拉普拉斯算子是一样的。也就是说拉普拉斯矩阵就是图上的拉普拉斯算子,或者说是离散的拉普拉斯算子。**
如果f是欧式空间中的二阶可微实函数,则△f即欧式空间中求其二阶微分(散度)
如果f是图上定义的一组高维向量,则Lf即在图空间中求其二阶微分(散度),L是图的拉普拉斯矩阵
- 散度(标量)
**设向量场 **A(x,y,z) = P(x,y,z) i + Q(x,y,z) j + R(x,y,z) k,则其散度为
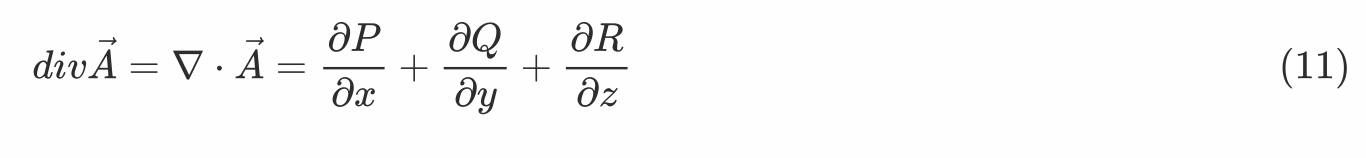
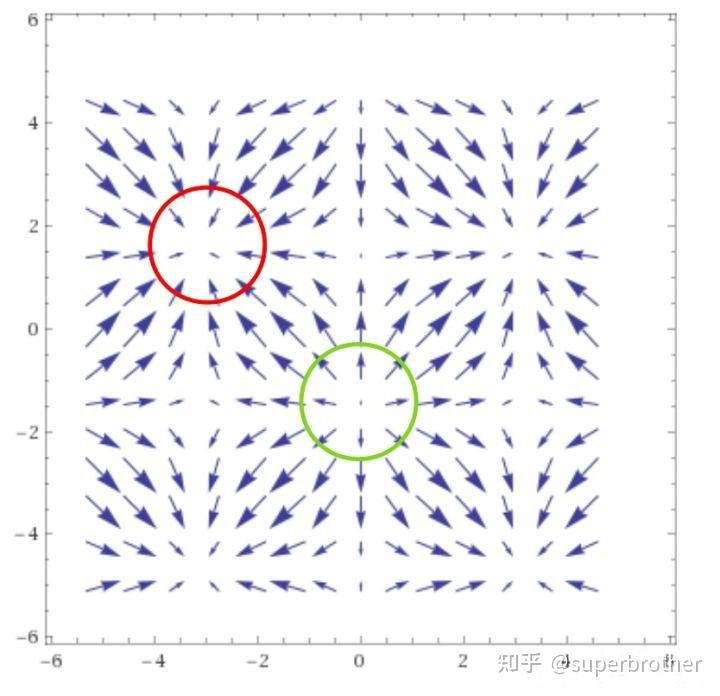
div A>0时,****表示该点有散发通量的正源(发散源)。如下图中绿圈所示,即为散度大于0的点,其附近的矢量场情况
**div A<0时,****表示该点有吸收通量的负源(洞或汇)。**如下图中红圈所示,即为散度小于0的点,其附近的矢量场情况。
**div A=0时,**该点无源
-
离散函数的导数
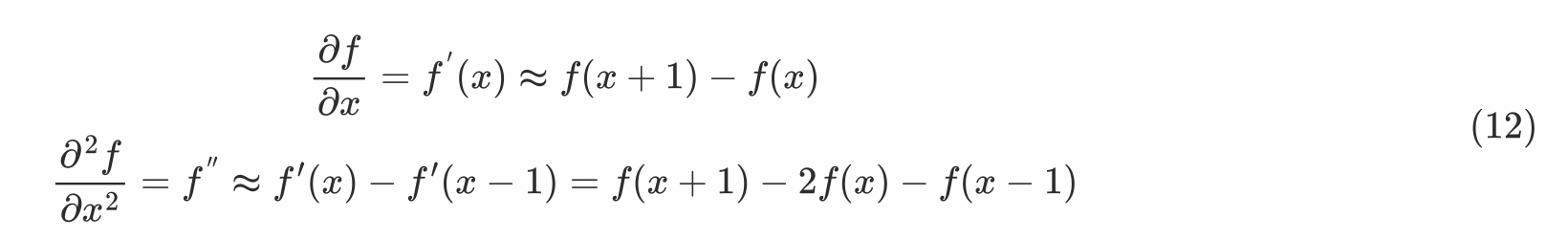
-
根据上面的离散函数的导数形式,Laplacian算子转换为离散形式
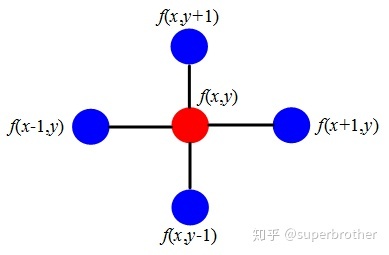
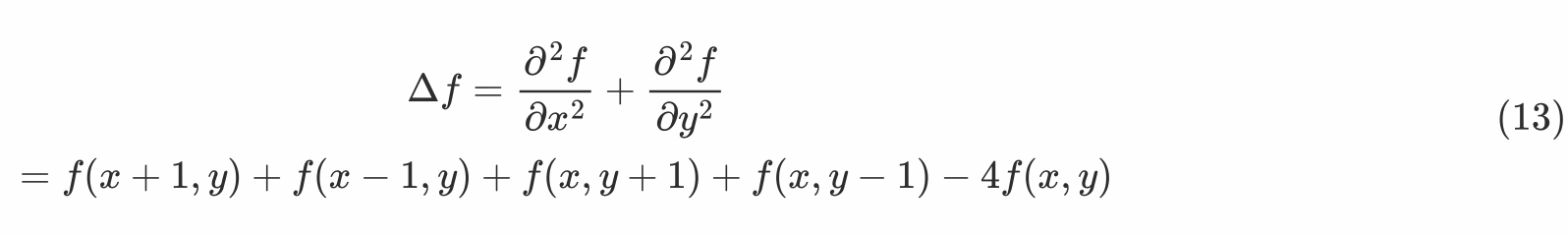
拉普拉斯算子计算了周围点与中心点的梯度差。当f(x,y)受到扰动后,可能变为相邻的f(x-1,y)等4个节点之一,拉普拉斯算子得到的是对该点进行微小扰动后可能获得的总增益 (或者说是总变化)
-
现在,将此结论推广到图
** 假设具有N个节点的图G,此时以上定义的函数f是N维向量,f=(f1,f2,f3,...,fN),其中fi为函数f在节点i处的函数值。类比于f(x,y)在节点(x,y)处的值。对i节点进行扰动,它可能变为任意一个与它相邻的节点j∈Ni,Ni表示节点i的一阶邻域节点。**
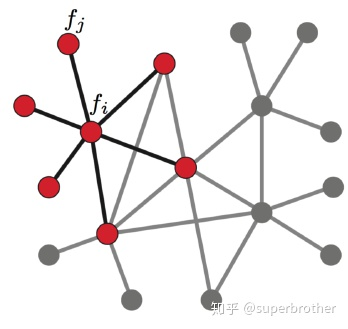
拉普拉斯算子可以计算一个点到它所有自由度上微小扰动的增益,则通过图来表示就是任意一个节点j变化到节点i所带来的增益,设边Eij具有权重wij,当wij=0时,表示结点i和j不相邻。由此,对应的Laplacian算子可定义为: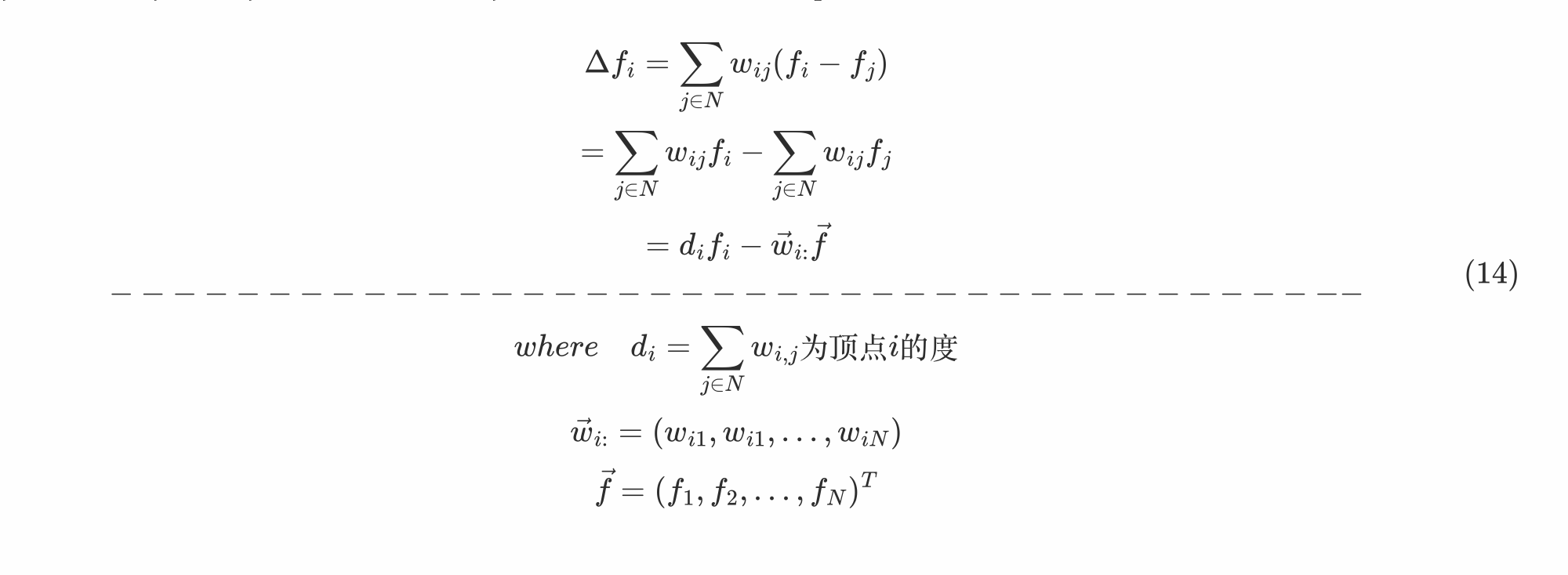
那么,对于所有的N个节点,其Laplacian算子为
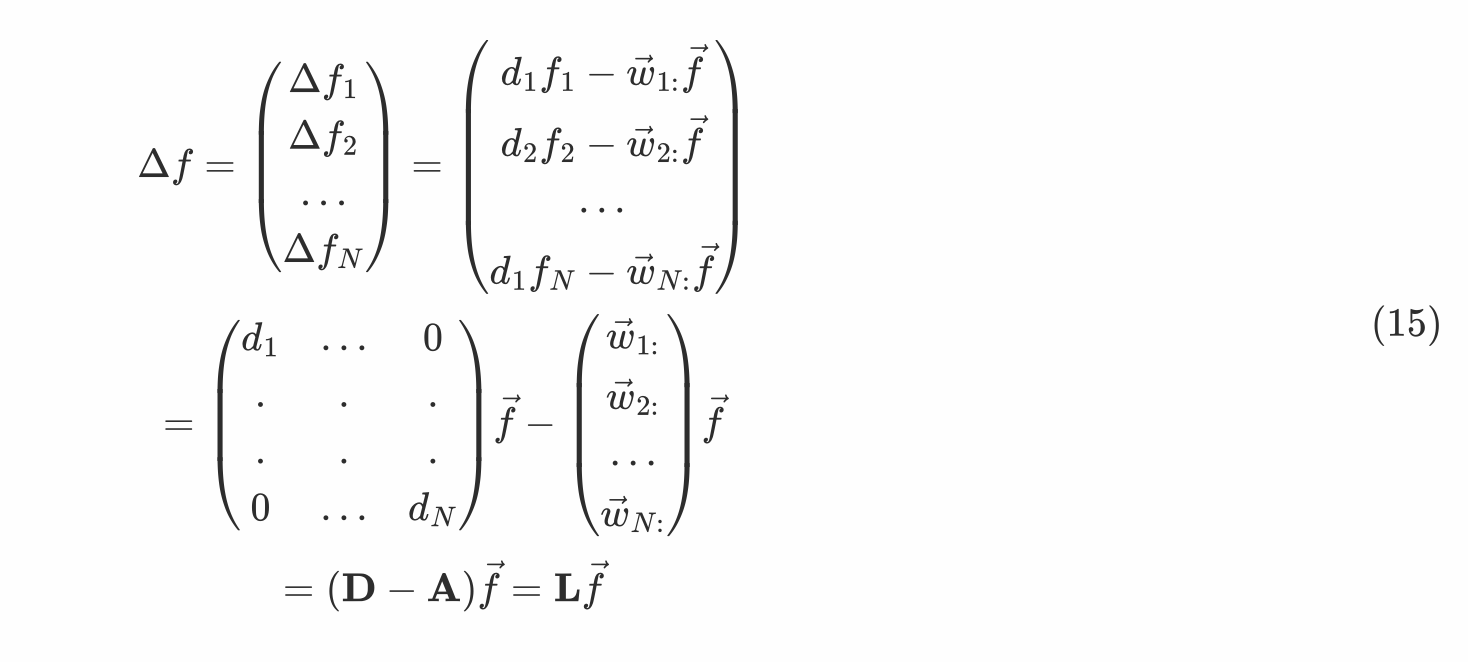
上式中的两个矩阵
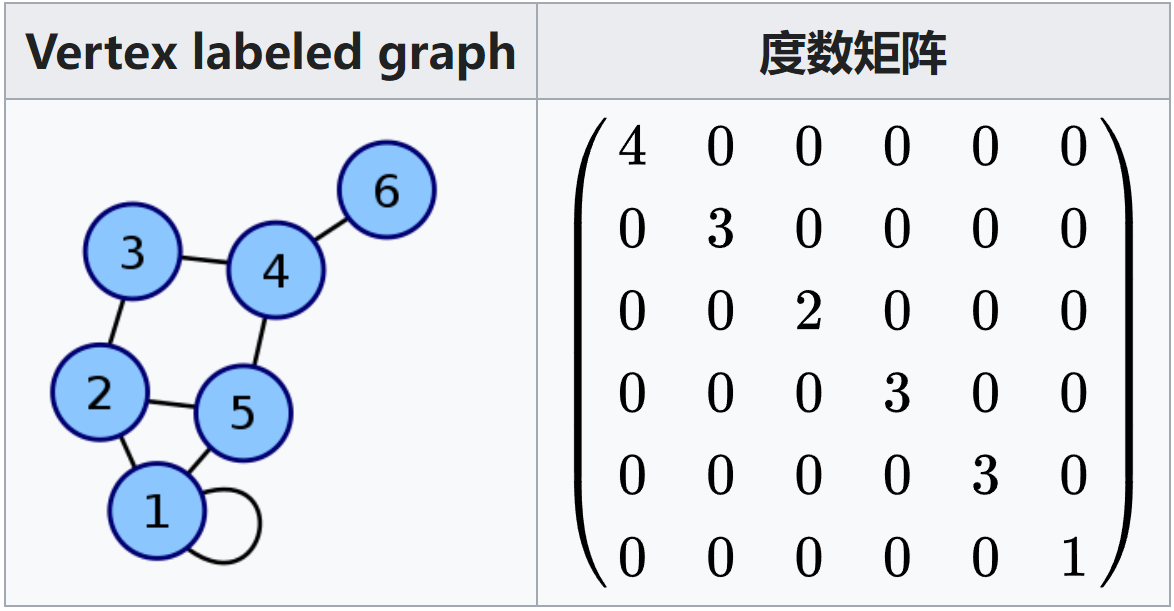
矩阵****D:图的度数矩阵
矩阵****A:图的邻接矩阵
对图的Laplacian算子使用标准化,对A的每一行除以行的和(即结点的度),得到标准化的A,用矩阵表示为:

在实际中,使用的是对称标准化:

==****因此,图的Laplacian算子可写为:==

3.3 总结
这里(D-W)就是拉普拉斯矩阵L。根据前面所述,拉普拉斯矩阵中的第i行实际上反应了第i个节点在对其他所有节点产生扰动时所产生的增益累积。
直观上来讲,图拉普拉斯反映了当在节点i上施加一个势,这个势以****哪个方向能够多顺畅的流向其他节点。
4. Graph Fourier
**定义Laplacian算子的目的==是为了找到Fourier变换的基==。**
传统Fourier变换的基,如下,就是Laplacian算子的一组特征向量。

那么图的Fourier基就是 L矩阵的n个特征向量U=(****u1,...,un),L可以分解为:

其中Λ是特征值组成的对角矩阵,则有:

类比传统Fourier变换之下,Graph Fourier变换可以定义为

**用矩阵形式表示Graph Fourier变换 (==图的傅里叶变换定义==)**

类似地,Inverse Graph Fourier变换定义为

**用矩阵形式表示: (==图的傅里叶逆变换定义==)**

**==需要注意的是==:**
图傅里叶变换使用的变换矩阵,并不同于离散傅里叶变换。离散傅里叶变换所用矩阵形式固定,如下:y=Fx
其中
此矩阵F称为傅里叶矩阵。
而图傅里叶中所用矩阵随图结构的不同而变化,因此二者不能混为一谈。
因此图傅里叶变换并不是通过严谨的数学推导,将傅里叶变换扩展到图上,而是经过许多类比,直接给出如此定义。傅里叶变换是以拉普拉斯算子的特征向量为基进行投影,那么图傅里叶变换就以拉普拉斯矩阵的特征向量为基进行投影。
5. Graph Convolution
根据卷积定理,则图卷积公式可表示为:

x为卷积核,将x的fourier变换(U^T x)看做是L矩阵特征值的函数
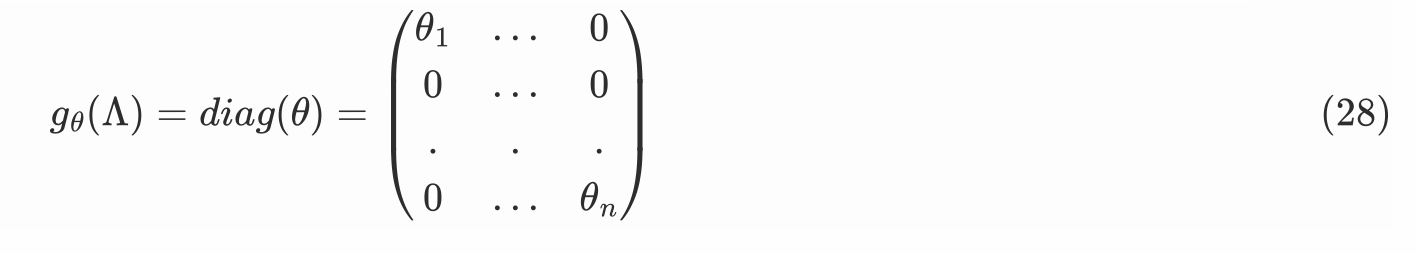
θ为待学习的参数,即weights,初始化后通过损失函数反向传播后更新得出神经网络计算公式: