一、因子分解机
1. 介绍
因子分解机于2010年由Steffen Rendle提出,是一种推荐模型,可用于解决推荐系统中的推荐问题。
因子分解机通过将用户和物品表示为向量,然后使用向量乘积来预测用户对物品的兴趣度。
与传统机器学习算法相比,因子分解机具有以下优点:
支持高维稀疏数据:因子分解机可以处理大量的用户和物品,而且在处理高维稀疏数据时,因子分解机可以更好地发挥其优势。
模型复杂度低:因子分解机的复杂度比其他推荐模型低,使得推荐系统能够更快地处理大规模的数据集。
可以学习用户和物品的隐式特征:因子分解机可以学习用户和物品的隐式特征,这些特征是推荐系统中非常重要的。
2. 演化

2.1 线性模型
简单的线性模型是对所有特征的加权组合;其中需要估计的参数包括𝑤0、𝑤∈ℝ^𝑛, 𝑛是特征维度
缺点:线性模型仅用来单一的特征,没有考虑到特征之间的关系,因此表达能力有限

2.2 POLY2
POLY2(Degree-2 Polynomial Margin):在线性模型中加入二阶交叉特征;其中需要估计的参数包括𝑤0、𝑤∈ℝ^𝑛、 𝑤^𝑇 𝑤∈ℝ^(𝑛×𝑛) , 𝑛是特征维度;参数个数为1+𝑛+𝑛(𝑛−1)/2
缺点:复杂度上升;在数据中不是每个特征组合都相互作用,此时𝑥𝑖 𝑥𝑗为0,矩阵稀疏,训练难以收敛

2.3 因子分解机
为每个特征学习了一个隐权重向量,在特征交叉的时候,用特征隐向量内积作为交叉特征的权重;其中需要估计的参数包括𝑤0、𝑤∈ℝ^𝑛、𝑉∈ℝ^(𝑛×𝑘) ,n是特征维度,k是隐向量维度;参数个数为1+𝑛+𝑘𝑛
优势:二阶交叉特征的系数不再是独立无关的,同时解决数据稀疏导致的无法训练参数的问题
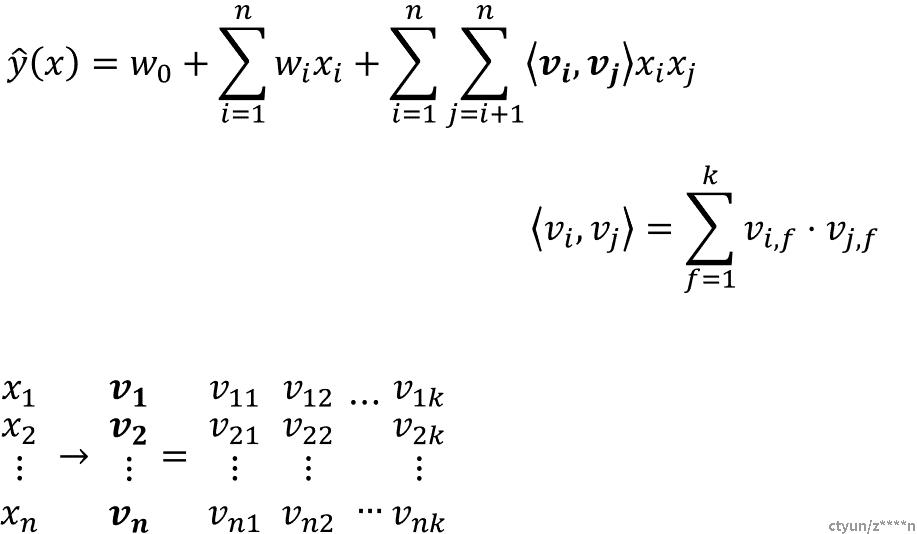
3. 因子分解机模型求解
交叉项的计算可以简化为线性复杂度的计算,由O(kn^2)降低到O(kn)

利用梯度下降算法(SGD等)来训练,迭代更新参数的公式

4. 因子分解机拓展
- 高阶分解机:叉项拓展到最多d(d>2)个特征的交叉,将时间复杂度改进到线性时间
- FFM(Field-aware Factorization Machine):每个特征都用 f 个隐向量来描述,二阶交叉参数从kn上升到fkn
二、纵向联邦因子分解机
1. 应用示例

partyA持有用户书籍相关偏好信息,partyB持有用户兴趣信息
联邦纵向因子分解机使数据不出本地的情况下,对两方重叠的用户进行因子分级机建模
2. 建模
①:party A内部做特征交叉,利用A独有的特征数据
②:party B内部做特征交叉,利用B独有的特征数据
③:将AB特征做二阶交叉

模型输出:基于A交叉特征的模型结果+基于AB交叉特征的模型结果+基于B交叉特征的模型结果
