特点： 每件物品仅用一次

N件物品，容量为V的背包。每件物品只能用一次。每个物品的价值为w

将dp[i]表示的所有选法分成两大类（划分原则：不漏）

① 选法中不含 i ， 即从 1 ~ i-1中选，且总体积不超过j，即 dp[i-1]

② 选法中包含 i ，即从 1 ~ i 中选，包含 i，且总体积不超过 j

可以先把第 i 个物品拿出来，即从第 1 ~ i-1中选，且总体积不超过 j-v[i]。

所以状态转移方程为：f[i][j] = f[i - 1][j]; 
                                    if (j >= v[i]) f[i][j] = max(f[i][j], f[i - 1][j - v[i]] + w[i]);

#include<bits/stdc++.h>
using namespace std;
const int N = 1010;
int f[N][N];
int v[N], w[N];
int n, m;
int main()
{
    ios::sync_with_stdio(false);
    cin.tie(0);
    cout.tie(0);

    cin >> n >> m;
    for (int i = 1; i <= n; i++) cin >> v[i] >> w[i];

    for (int i = 1; i <= n; i++) {
        for (int j = 1; j <= m; j++) {
            f[i][j] = f[i - 1][j];
            if (j >= v[i]) f[i][j] = max(f[i][j], f[i - 1][j - v[i]] + w[i]);
        }
    }

    cout << f[n][m] << '\n';
}

这里dp数组不需要初始化是因为在全局中全初始化为0了，所以状态转移时没有影响。

注意这里是不能直接将第二层循环的j赋值为v[i]

因为在二维状态表示下f[i][j]和f[i - 1][j]是互不影响的，在j < v[i]的情况下f[i][j]有些是不应该为0的而却无法被更新到，如果f[i][j]不通过f[i - 1][j]更新，那么f[i][j]就永远是0，那么在这种情况下f[i][j]就恒被更新为 f[i - 1][j - v[i]] + w[i]导致错误。

接着就是从二维优化成一维。一维的dp数组表示的就是容量为多少时，价值最大。

优化成一维就是将原本二维dp数组中的dp[i][]删除。

//01背包
#include<iostream>
using namespace std;
const int N = 1e3 + 9;
int dp[N], v[N], w[N], n, m;

int main()
{
	ios::sync_with_stdio(0), cin.tie(0), cout.tie(0);
	cin >> n >> m;
	for (int i = 1; i <= n; ++i) cin >> v[i] >> w[i];

	for (int i = 1; i <= n; ++i)
	{
		for (int j = m; j >= v[i]; --j)
		{
			dp[j] = max(dp[j], dp[j - v[i]] + w[i]);
		}
	}
	//状态dp[j]定义：N件物品，背包容量j下的最优解。
	//初始化时将dp[0]和dp[j]都初始化为0，当容量 <= m时为最大价值
	//初始化时将dp[0]初始化为0，dp[j]都初始化为-INF，当容量恰好等于m时为最大价值
	cout << dp[m];
	return 0;
}

上述代码必须满足倒序遍历因为：

当J从小到大递增时，每次J都可以基于J - vi算出来
但是我忽略了一个问题：
当J从小到大递增时，i是不变的，也就是说基于J - vi求出来的J都是同一个i
如果用没有降维之前来表示的话是这样的： f[i][j] = max(f[i][j], f[i][j - v[i])
但正确的表示方式应该是这样的： f[i][j] = max(f[i][j], f[i - 1][j - v[i])
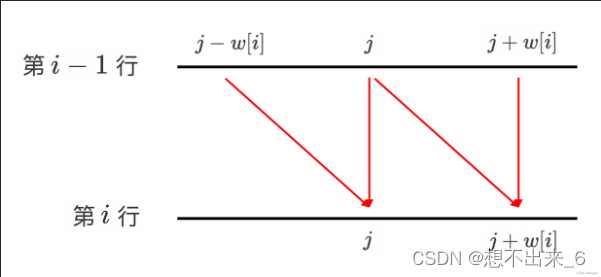
那为什么当J从大到小更新时就可以满足了呢？
加入还是计算f[j]，同样的想要计算J还是要基于J - vi, 此时元素个数是 i
由之前的二维模式可以知道 要计算f[i][j]需要基于f[i - 1][j - vi]来求得

由于J是降序的，也就是说当计算J时，J - vi还没有被更新（J - vi < J），
也就是说此时的 J - vi对应的还是上一轮的i - 1，正好可以满足需求
所以J只能是从大到小来遍历。

上面说二维时第二层循环j不可以从v[i]开始遍历。

原因：

为什么一维状态表示就对呢。因为在一维状态下f[j]在当前循环下表示为f[i][j]，在上一循环下表示为f[i - 1][j]，也是说在当前循环下f[j]在被赋值之前的值就已经是f[i - 1][j]了，相当于默认被f[i - 1][j]更新了，这也就是优化为一维后被删掉的那个恒等式f[j] = f[j]

这是y总评论区的解答：