一、46. 全排列
中等
给定一个不含重复数字的数组 nums ,返回其 所有可能的全排列 。你可以 按任意顺序 返回答案。
示例 1:
输入:nums = [1,2,3]
输出:[[1,2,3],[1,3,2],[2,1,3],[2,3,1],[3,1,2],[3,2,1]]
示例 2:
输入:nums = [0,1]
输出:[[0,1],[1,0]]
示例 3:
输入:nums = [1]
输出:[[1]]
提示:
1 <= nums.length <= 6
-10 <= nums[i] <= 10
nums 中的所有整数 互不相同
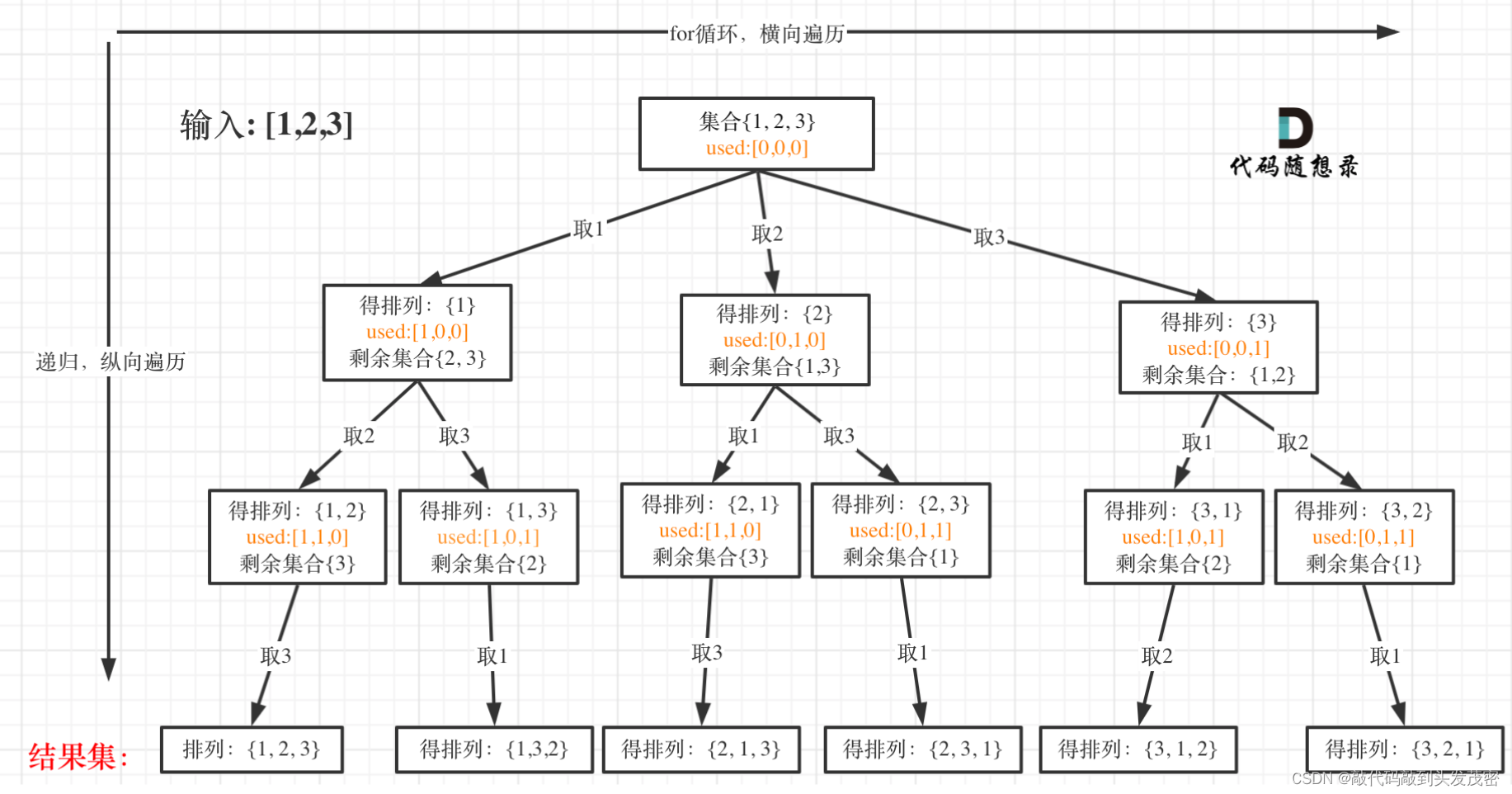
1、以[1,2,3]为例,抽象成树形结构
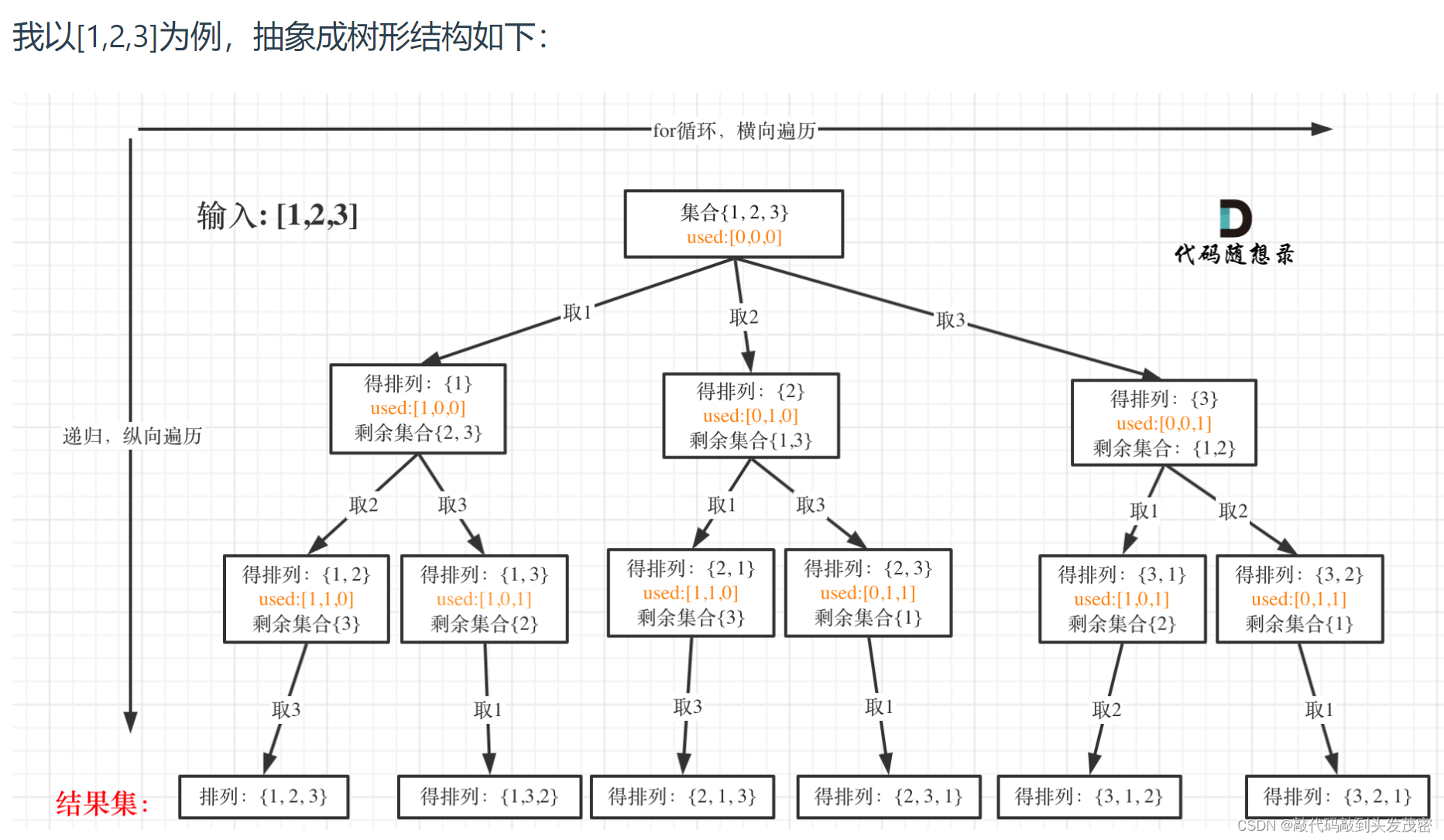
2、回溯三部曲
1、递归函数参数
首先排列是有序的,也就是说 [1,2] 和 [2,1] 是两个集合,这和之前分析的子集以及组合所不同的地方。
可以看出元素1在[1,2]中已经使用过了,但是在[2,1]中还要在使用一次1,所以处理排列问题就不用使用startIndex了。
但排列问题需要一个used数组,标记已经选择的元素,如图橘黄色部分所示:
2、递归终止条件
可以看出叶子节点,就是收割结果的地方。
那么什么时候,算是到达叶子节点呢?
当收集元素的数组path的大小达到和nums数组一样大的时候,说明找到了一个全排列,也表示到达了叶子节点。
3、单层搜索的逻辑
这里和77.组合问题、131.切割问题和78.子集问题最大的不同就是for循环里不用startIndex了。
因为排列问题,每次都要从头开始搜索,例如元素1在[1,2]中已经使用过了,但是在[2,1]中还要再使用一次1。
而used数组,其实就是记录此时path里都有哪些元素使用了,一个排列里一个元素只能使用一次。
class S46:
def func(self, nums):
result = []
def dfs(path, used):
if len(path) == len(nums):
result.append(path[:])
return
for i in range(len(nums)):
if used[i] == True:
continue
used[i] = True
path.append(nums[i])
dfs(path, used)
used[i] = False
path.pop()
dfs([], [False] * len(nums))
return result
r = S46()
nums = [1, 2, 3]
print(r.func(nums))
二、LCR 084. 全排列 II
中等
给定一个可包含重复数字的整数集合 nums ,按任意顺序 返回它所有不重复的全排列。
示例 1:
输入:nums = [1,1,2]
输出:
[[1,1,2],
[1,2,1],
[2,1,1]]
示例 2:
输入:nums = [1,2,3]
输出:[[1,2,3],[1,3,2],[2,1,3],[2,3,1],[3,1,2],[3,2,1]]
还要强调的是去重一定要对元素进行排序,这样我们才方便通过相邻的节点来判断是否重复使用了。
1、以[1,1,2]为例,抽象成树形结构
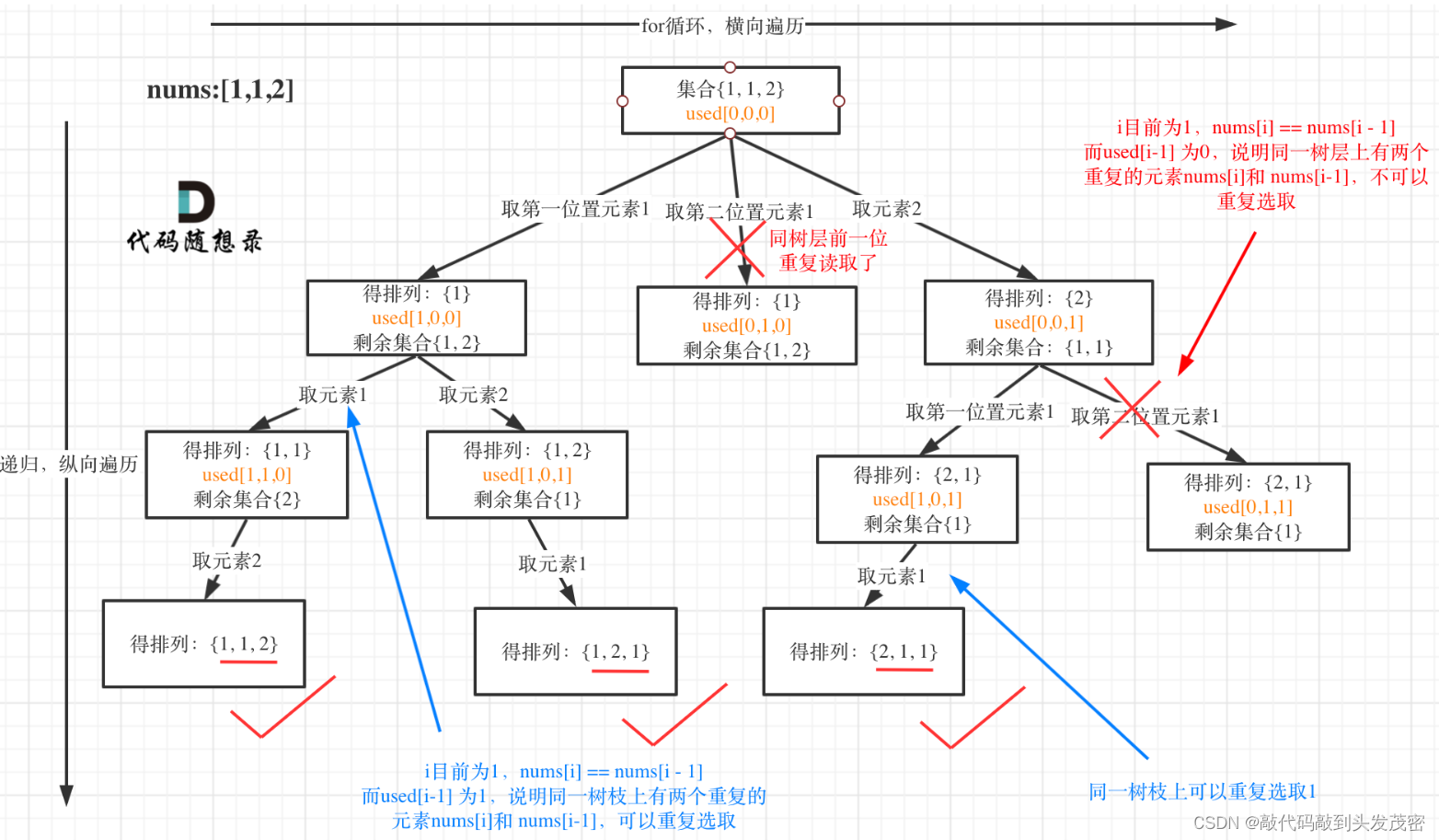
图中我们对同一树层,前一位(也就是nums[i-1])如果使用过,那么就进行去重。
一般来说:组合问题和排列问题是在树形结构的叶子节点上收集结果,而子集问题就是取树上所有节点的结果。
去重最为关键的代码为:
if i > 0 and nums[i] == nums[i - 1] and used[i - 1] == False:
class S47:
def func(self,nums):
nums.sort()
result=[]
def dfs(path,used):
if len(path)==len(nums):
result.append(path[:])
return
for i in range(len(nums)):
#todo 如果当前值与上一个值相等,进行减枝操作;并且上一个值没有使用
# 前一位是1,只有回溯,前一位才能置为0
# 竖层:因为前一位是1,回溯到0 used=[1,0,0]——》used=[0,1,0]
if i>0 and nums[i]==nums[i-1] and used[i-1]==False:
continue
if used[i]==True: #细节:为了防止再次取当前值
continue
used[i]=True
path.append(nums[i])
dfs(path,used)
used[i]=False
path.pop()
dfs([],[False]*len(nums))
return result
r=S47()
nums=[1,1,2]
print(r.func(nums))
三、面试题 08.07. 无重复字符串的排列组合
中等
无重复字符串的排列组合。编写一种方法,计算某字符串的所有排列组合,字符串每个字符均不相同。
示例1:
输入:S = “qwe”
输出:[“qwe”, “qew”, “wqe”, “weq”, “ewq”, “eqw”]
示例2:
输入:S = “ab”
输出:[“ab”, “ba”]
提示:
字符都是英文字母。
字符串长度在[1, 9]之间。
class S46:
def func(self,nums):
result=[]
def dfs(nums,path,used):
#终止条件
if len(path)==len(nums):
result.append(path[:])
return
for i in range(len(nums)):
if used[i]==True:
continue
used[i]=True
path.append(nums[i])
dfs(nums,path,used)
path.pop()
used[i]=False
dfs(nums,[],[False]*len(nums))
res=[''.join(i) for i in result]
return res
r=S46()
nums="ab"
print(r.func(nums))
四、面试题 08.08. 有重复字符串的排列组合
中等
有重复字符串的排列组合。编写一种方法,计算某字符串的所有排列组合。
示例1:
输入:S = “qqe”
输出:[“eqq”,“qeq”,“qqe”]
示例2:
输入:S = “ab”
输出:[“ab”, “ba”]
提示:
字符都是英文字母。
字符串长度在[1, 9]之间。
class S0808:
def func(self,nums):
result=[]
def dfs(path,used):
if len(nums)==len(path):
result.append(path[:])
return
for i in range(len(nums)):
if i>0 and nums[i]==nums[i-1] and used[i-1]==False:
continue
if used[i]==True:
continue
used[i]=True
path.append(nums[i])
dfs(path,used)
used[i]=False
path.pop()
dfs([],[False]*len(nums))
return [''.join(i) for i in result]
r=S0808()
nums="qqe"
print(r.func(nums))

