栈
栈的概念及结构
栈(Stack) :一种特殊的线性表,其只允许在固定的一端进行插入和删除元素操作。进行数据插入和删除操作的一端称为栈顶,另一端称为栈底。栈中的数据元素遵守后进先出LIFO(Last In First Out)的原则。类似于一个垂直摞起来的盘子,想要拿或放只能从顶上,而不能从底部操作。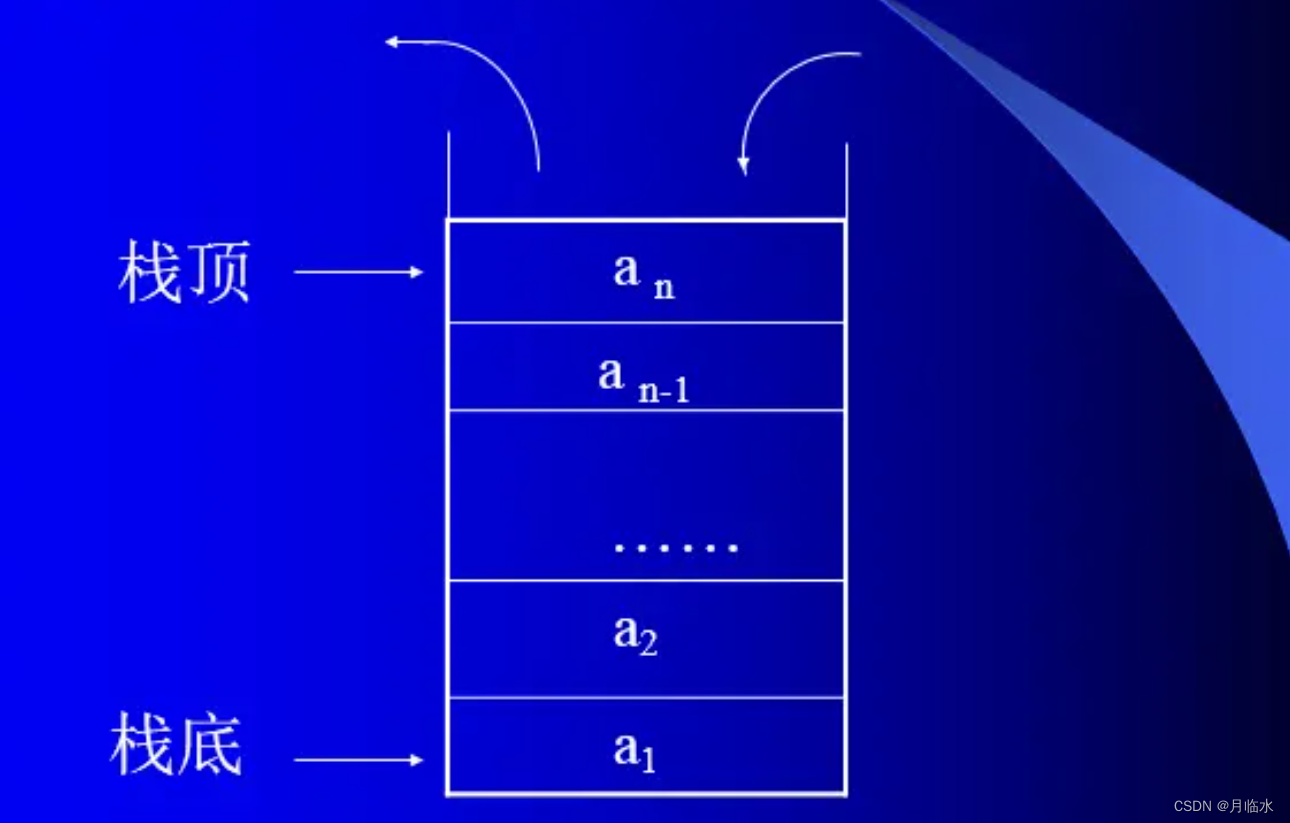
栈的一些操作
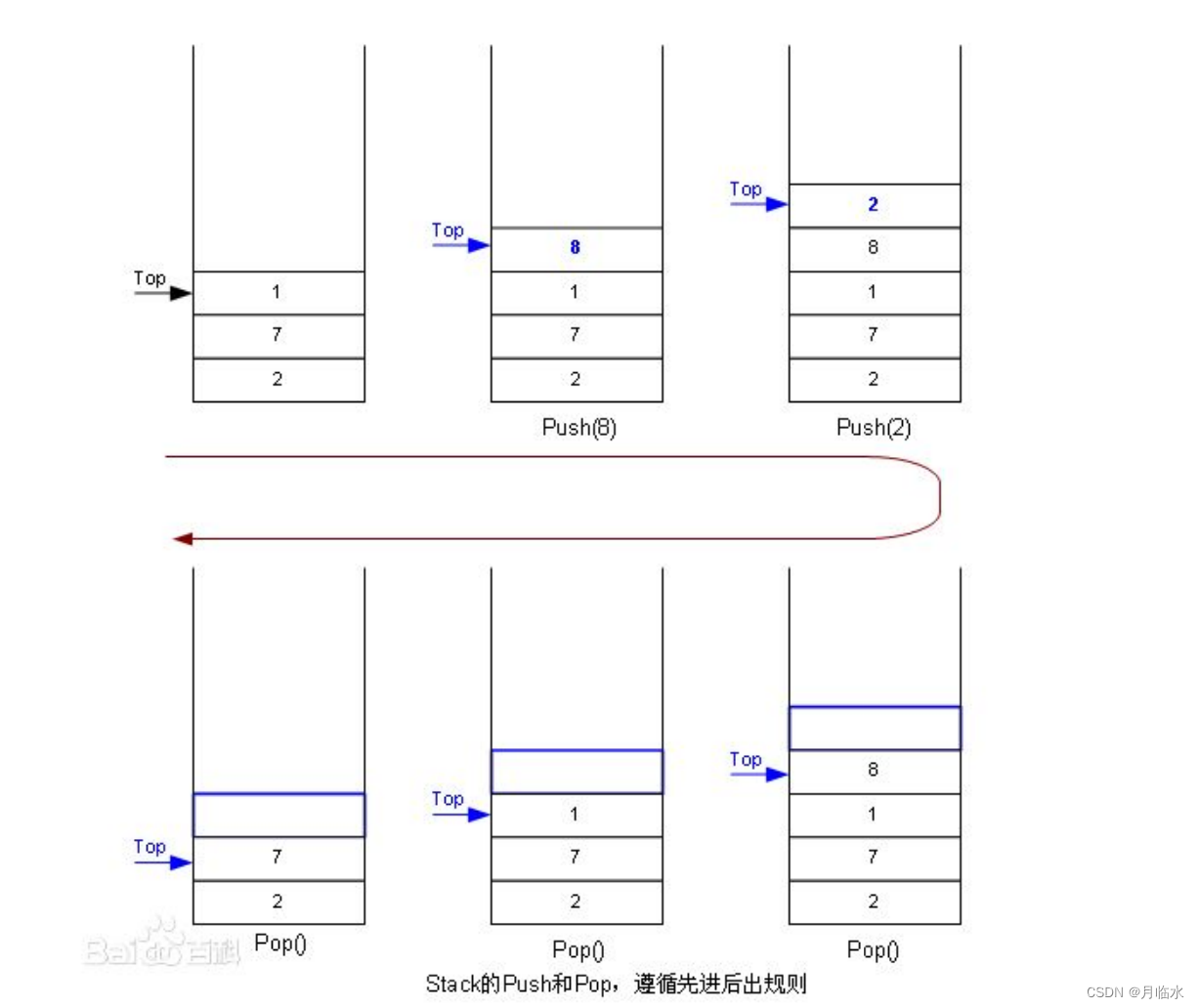
压栈(push):栈的插入操作叫做进栈/压栈/入栈,入数据在栈顶。
出栈(pop):栈的删除操作叫做出栈。出数据也在栈顶
获取栈顶元素(top):获取栈顶元素,但不将其从栈中移除。
判断栈是否为空(isEmpty):判断栈是否为空操作会返回一个布尔值,表示栈是否为空。
栈的实现
顺序栈
顺序栈是一种基于数组实现的栈数据结构。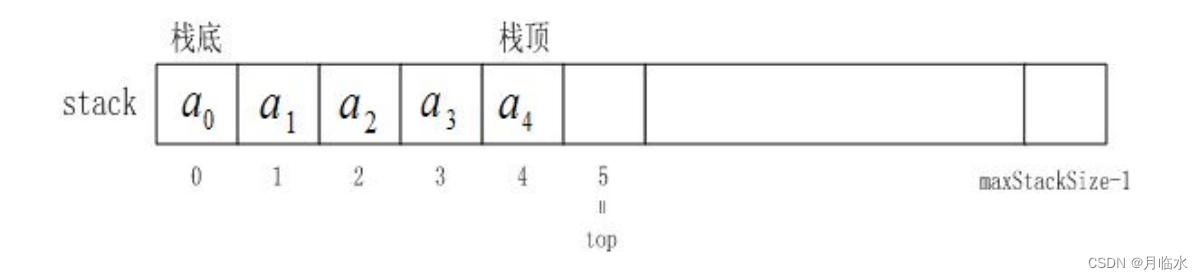
代码实现
//准备工作
int[] array;
int size;//当前栈内的空间大小
//创建栈,为栈分配存储空间
public MyStack() {
array = new int[3];
}
//入栈
public void push(int val) {
//检查是否需要扩容
ensureCapacity();
//入栈,并将栈的大小自增1
array[size++] = val;
}
//出栈
public int pop() {
//因为top()方法中已经检查了栈是否为空,所以这里就不再检查了
int val = top();
size--;
return val;
}
//判断栈是否为空
public boolean isEmpty() {
return size == 0;
}
//获取栈顶元素
public int top() {
if (isEmpty()) {
System.out.println("栈为空!");
return -1;//这里也可以写成抛出一个异常
}
return array[size - 1];
}
//检查扩容
public void ensureCapacity() {
//检查栈是否已满
if (size == array.length) {
//已满,将栈的容量扩大一倍
array = Arrays.copyOf(array, size * 2);
}
}
链栈
采用链式存储结构实现的栈称为链栈,链栈通常采用单链表来实现,因此其结构与单链表的结构相同由于栈的插入和删除操作仅限制在栈顶位置进行,所以采用单链表的表头指针作为栈顶指针。
代码实现
//准备工作
private Element base;//栈底指针
private Element top;//栈顶指针
//栈中的每个节点
private class Element {
private int data;
private Element next;
}
//入栈
public void push(int val) {
Element newElem = new Element();
newElem.data = val;
newElem.next = top;
top = newElem;
}
//出栈
public int pop() {
if(isEmpty()) {
System.out.println("栈为空!");
return -1;//这里也可以抛出异常
}
int val = top.data;
top = top.next;
return val;
}
//判断栈是否为空
public boolean isEmpty() {
//栈底指针和栈顶指针指向同一位置,此时栈为空
return base == top;
}
//获取栈顶元素
public int top() {
return top.data;
}
栈小结
⭐栈的特点是?
先进后出
⭐顺序栈与链栈哪个更好?
顺序栈和链栈各有优缺点,没有绝对的“更好”。选择哪种实现方式取决于问题的要求和特点。
⭐顺序栈(数组实现)的优点是:
- 存储空间连续,可以利用数组的随机访问特性,对栈的操作具有较高的效率。
- 实现简单,代码量较少。
⭐顺序栈(数组实现)的缺点是:
- 存储空间固定,创建栈时必须指定大小,大小无法动态调整。
- 当栈满时需要进行扩容,需要重新分配更大的内存空间,并将原有数据复制到新的内存空间中。
⭐链栈的优点是:
- 存储空间可以动态分配,不受固定大小的限制。
- 插入和删除元素的操作只需要修改指针,不需要移动大量的数据,相对较快。
⭐链栈的缺点是:
- 需要额外的指针指向下一个节点,增加了存储空间的开销。
- 由于每个节点需要存储指针,导致链栈的存储密度较低,对内存的利用率较低。
有关栈的一些题
1. 有效的括号
题目链接: 有效的括号
题目
给定一个只包括 ‘(’,‘)’,‘{’,‘}’,‘[’,‘]’ 的字符串 s ,判断字符串是否有效。
有效字符串需满足:
左括号必须用相同类型的右括号闭合。
左括号必须以正确的顺序闭合。
每个右括号都有一个对应的相同类型的左括号。
-
示例 1:
输入:s = “()”
输出:true -
示例 2:
输入:s = “()[]{}”
输出:true -
示例 3:
输入:s = “(]”
输出:false
提示:
1 <= s.length <= 104
s 仅由括号 ‘()[]{}’ 组成
思路
- 遍历字符串中的每个字符。
- 如果字符是一个开括号(即’(', ‘[’, ‘{’),它会被压入栈中。
- 如果字符是一个闭括号,则检查栈是否为空。如果栈为空,意味着没有相应的开括号,字符串无效。如果栈不为空,则检查栈的顶部是否包含相应的开括号。如果是,栈的顶部元素将被弹出。如果不是,意味着字符串无效。
- 在遍历字符串的所有字符之后,检查栈是否为空。如果栈为空,意味着所有的开括号已经匹配并从栈中弹出,字符串有效。如果栈不为空,意味着还有剩余的开括号,字符串无效。
代码
class Solution {
public boolean isValid(String s) {
Stack<Character> stack = new Stack<>();
for(int i = 0; i < s.length(); i++) {
char ch = s.charAt(i);
if(ch == '(' || ch == '[' || ch == '{') {
stack.add(ch);
}else {
if(stack.isEmpty()){
return false;
}else {
if (ch == ')' && stack.peek() == '(' ||
ch == ']' && stack.peek() == '[' ||
ch == '}' && stack.peek() == '{' ) {
stack.pop();
} else {
return false;
}
}
}
}
return stack.isEmpty();
}
}
2. 逆波兰表达式求值
题目链接: 逆波兰表达式求值
题目
给你一个字符串数组 tokens ,表示一个根据 逆波兰表示法 表示的算术表达式。
请你计算该表达式。返回一个表示表达式值的整数。
注意:
有效的算符为 ‘+’、‘-’、‘*’ 和 ‘/’ 。
每个操作数(运算对象)都可以是一个整数或者另一个表达式。
两个整数之间的除法总是 向零截断 。
表达式中不含除零运算。
输入是一个根据逆波兰表示法表示的算术表达式。
答案及所有中间计算结果可以用 32 位 整数表示。
-
示例 1:
输入:tokens = [“2”,“1”,“+”,“3”,“*”]
输出:9
解释:该算式转化为常见的中缀算术表达式为:((2 + 1) * 3) = 9 -
示例 2:
输入:tokens = [“4”,“13”,“5”,“/”,“+”]
输出:6
解释:该算式转化为常见的中缀算术表达式为:(4 + (13 / 5)) = 6 -
示例 3:
输入:tokens = [“10”,“6”,“9”,“3”,“+”,“-11”,““,”/“,””,“17”,“+”,“5”,“+”]
输出:22
解释:该算式转化为常见的中缀算术表达式为:
((10 * (6 / ((9 + 3) * -11))) + 17) + 5
= ((10 * (6 / (12 * -11))) + 17) + 5
= ((10 * (6 / -132)) + 17) + 5
= ((10 * 0) + 17) + 5
= (0 + 17) + 5
= 17 + 5
= 22
提示:
1 <= tokens.length <= 104
tokens[i] 是一个算符(“+”、“-”、“*” 或 “/”),或是在范围 [-200, 200] 内的一个整数
思路
用循环遍历整个字符串数组,如果当前字符为数字,则入栈;如果当前字符为运算符,则将栈中的两个数字弹出,根据运算符参与相应的运算。最后栈当中会剩余一个最终结果,return返回这个结果。
代码
class Solution {
public boolean isOperation(String tmp) {
return tmp.equals("+") || tmp.equals("-") ||tmp.equals("*") ||tmp.equals("/");
}
public int evalRPN(String[] tokens) {
Stack<Integer> stack = new Stack<>();
for(int i = 0; i < tokens.length; i++) {
String tmp = tokens[i];
if(!isOperation(tmp)) {
stack.add(Integer.valueOf(tmp));
} else {
int num2 = stack.pop();
int num1 = stack.pop();
switch (tmp) {
case "+":
stack.push(num1 + num2);
break;
case "-":
stack.push(num1 - num2);
break;
case "*":
stack.push(num1 * num2);
break;
case "/":
stack.push(num1 / num2);
break;
}
}
}
return stack.pop();
}
}
3. 栈的压入、弹出序列
题目链接:栈的压入、弹出序列
题目
描述
输入两个整数序列,第一个序列表示栈的压入顺序,请判断第二个序列是否可能为该栈的弹出顺序。假设压入栈的所有数字均不相等。例如序列1,2,3,4,5是某栈的压入顺序,序列4,5,3,2,1是该压栈序列对应的一个弹出序列,但4,3,5,1,2就不可能是该压栈序列的弹出序列。
- 0<=pushV.length == popV.length <=1000
- -1000<=pushV[i]<=1000
- pushV 的所有数字均不相同
示例1
输入:[1,2,3,4,5],[4,5,3,2,1]
返回值:true
说明:可以通过push(1)=>push(2)=>push(3)=>push(4)=>pop()=>push(5)=>pop()=>pop()=>pop()=>pop()
这样的顺序得到[4,5,3,2,1]这个序列,返回true
示例2
输入:[1,2,3,4,5],[4,3,5,1,2]
返回值:false
说明:
由于是[1,2,3,4,5]的压入顺序,[4,3,5,1,2]的弹出顺序,要求4,3,5必须在1,2前压入,且1,2不能弹出,但是这样压入的顺序,1又不能在2之前弹出,所以无法形成的,返回false
思路
- 定义一个整型变量j用于指示出栈数组popV的位置,初始化为0;定义一个Stack对象stack来模拟入栈过程。
- 使用循环遍历入栈数组pushV,
- 如果当前入栈元素不等于出栈数组popV中指针j所指向的元素,则将当前入栈元素压入栈stack中。
- 如果当前入栈元素等于出栈数组popV中指针j所指向的元素,则进行出栈操作:
- 将指针j向后移动一位,表示出栈数组中的下一个元素。
- 检查栈顶元素是否与popV[j]相等,如果相等,则继续出栈,直到栈为空或者栈顶元素与popV[j]不相等。
- 判断最终栈是否为空:遍历结束后,如果栈为空,则说明入栈和出栈顺序是匹配的,返回true;否则返回false。
代码
import java.util.*;
public class Solution {
public boolean IsPopOrder(int[] pushV, int[] popV) {
int j = 0;
Stack<Integer> stack = new Stack<>();
for(int i = 0; i < pushV.length; i++) {
if(pushV[i] != popV[j]) {
stack.push(pushV[i]);
} else {
j++;
while(!stack.isEmpty() && j < popV.length && popV[j] == stack.peek()) {
j++;
stack.pop();
}
}
}
return stack.isEmpty();
}
}

