一、让我们开始与杨辉三角的奇妙之旅

        无论你是尝试理解复杂的数学概念，还是激发对编程的新鲜兴趣，杨辉三角总能作为一个引人注目的工具在理论和实践中起到无比重要的作用。更准确地说，它也被称为帕斯卡三角，从视觉和功能上都是一种数学艺术品。特性巧妙且小巧的杨辉三角以1为边界，并且在内部每一个数字都是它左上方和右上方的数之和。为了使这个理论更加贴近实际，我们可以将其用编程的方式来呈现，比如在C语言代码中利用二维数组结构来构建杨辉三角。简洁又优雅的代码符合我们的目的，通过控制循环结构，我们能轻易的在屏幕上打印出美丽的杨辉三角。

        接下来，让我们转换一个场景，看看一个你应该非常熟悉的游戏——弹珠抽奖游戏如何显现出杨辉三角的影子。弹珠抽奖游戏的特点在于其随机性和公平性，吸引你参与并期待它带来的惊喜。有个有趣的观察，如果我们将游戏的每个分叉看作是一个决策点——左或右，那么或许你已经发现这与杨辉三角有着密切的关联。弹珠抽奖游戏的过程就像是在杨辉三角中从顶部走到底部，每一步都只能选择向下或者向右下。这样看来，每次的抽奖结果都对应了杨辉三角中的一条路径，不是吗？

二、卓越的编程是有迹可循的   

        在编写杨辉三角和弹珠抽奖程序的过程中，我们需要有一些C语言的基石支撑，像是不同的数据类型（例如整型、浮点型）；还有表达式和各种运算符（赋值运算符、算术运算符等）的灵活运用，当然少不了诸如条件语句和循环语句这样的控制结构。在本案例中，我们还将学习如何使用数组来存储和处理一系列的数据。

        在编码的实践中，通过定义一个二维数组来存储杨辉三角，我们可以自由控制和处理数据，再借助循环结构，让我们轻松地填充这个二维数组来构建一个杨辉三角。再来看弹珠抽奖游戏，我们则可以设计一个模拟弹珠下落路径的算法。具体来说，就是模拟弹珠在每个节点向左还是向右的选择，最后在弹珠落点来确定奖项。

三、用C语言让杨辉三角熠熠生辉

        首先，在西方，这种三角形被称为帕斯卡三角，而在东方，我们称其为杨辉三角。对于杨辉三角的定义，你一定不陌生。简单来说，它是把二项式系数几何化表示，这就形成了一个等腰直角三角形，并且该三角形每行的数字都沿着两侧的边界对齐，内容则完全由其左上方和右上方两数之和构成。

        在C语言的世界里，二维数组就是实现杨辉三角的理想结构。它具有横向与纵向的特性，可以预留任何一行和一列的数据，非常适用于矩阵和其他二维数据的存储。在这个案例中，我们将二维数组视作工具，通过编码的方式存储杨辉三角的每个元素。

        接下来，我们将用到嵌套循环来遍历二维数组，将生成的元素填进去。其中，外部循环控制杨辉三角的行，内部循环处理特定行内的元素。借助杨辉三角的规则，我们可以轻松的描绘出三角形的每个元素，因为每个元素都等于它左上和右上的元素之和。

        当数据结构构建完毕，为了更加直观的观看到三角形的形状，我们有必要对其进行一定的调整使其美观。一种方式是在每一行前输出一些空格来实现对齐。随着行数的增加，需要的空格数逐渐减少，从而实现了杨辉三角的居中显示。

#include <stdio.h>

int main() {
    int n, i, j;

    printf("请输入杨辉三角的行数: ");
    scanf("%d", &n);

    int triangle[n][n];

    for(i = 0; i < n; i++) {
        triangle[i][0] = 1;
        triangle[i][i] = 1;
    }

    for(i = 2; i < n; i++) {
        for(j = 1; j <= i - 1; j++) {
            triangle[i][j] = triangle[i-1][j-1] + triangle[i-1][j];
        }
    }

    for(i = 0; i < n; i++) {
        for(j = 0; j < n-i-1; j++) {
            printf(" ");
        }
        for(j = 0; j <= i; j++) {
            printf("%d ", triangle[i][j]);
        }
        printf("\n");
    }

    return 0;
}

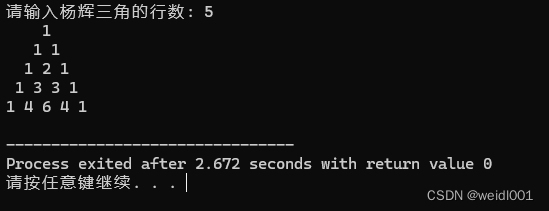
        这段代码片段先让用户读取需要输出的杨辉三角行数，接着根据用户的需求创建二维数组，并设定杨辉三角的边界条件和内部元素，最后通过空格的输出形成对齐的三角形，以此为用户带来更好的用户体验。

四、弹珠抽奖游戏的原理及其编程实现

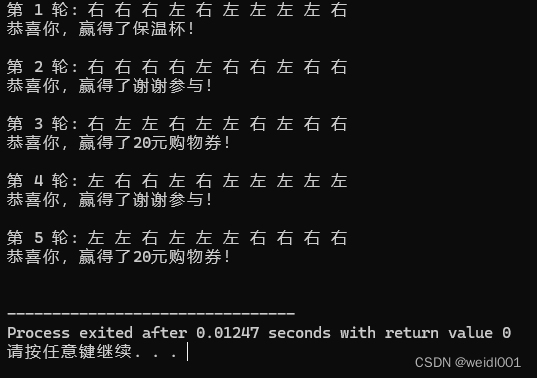
        弹珠抽奖游戏的原理很简单，弹珠从顶部开始下落，每遇到一个分叉点，弹珠都会随机选择左边或者右边的路径，最后落到一个奖品区域，弹珠落入的区域即为获得的奖品。

        在C语言中，我们可以用一维数组来表示奖品区域，数组中的每个元素代表一个奖品。然后，我们可以利用C语言中的随机函数来模拟弹珠的下落过程。在每个分叉点，生成一个0或1的随机数决定弹珠的下落方向。

        与杨辉三角类似，弹珠抽奖游戏的实现中也使用了数组和循环。然而，与杨辉三角不同的是，弹珠抽奖游戏中的数组是一维的，而杨辉三角中的数组是二维的。此外，弹珠抽奖游戏中的循环是用来模拟随机过程的，而杨辉三角中的循环是用来计算数值的。

#include <stdio.h>
#include <stdlib.h>
#include <time.h>

#define MAX 10 // 杨辉三角的最大行数
#define ROUNDS 5 // 抽奖的轮次

int main() {
    srand(time(NULL));  // 初始化随机数生成器
    int triangle[MAX][MAX] = {0};  // 用于存储每个位置的奖品索引
    // 定义一组更加日常化且多样化的奖品
    char* prizes[5] = {"1元话费", "10元购物券", "20元购物券", "保温杯", "谢谢参与"};

    // 构建杨辉三角（每个格子代表的奖品）
    for(int i = 0; i < MAX; i++) {
        for(int j = 0; j <= i; j++) {
            if (j == 0 || j == i) {  // 每一行的第一个和最后一个元素对应的奖品是"谢谢参与"
                triangle[i][j] = 4;
            } else {  // 其他元素对应的奖品随机
                triangle[i][j] = rand() % 5;
            }
        }
    }

    // 进行ROUNDS轮抽奖
    for(int round = 0; round < ROUNDS; round++) {
        int index = 0;  // 弹珠的初始位置
        printf("第 %d 轮: ", round + 1);

        // 模拟弹珠在杨辉三角中的路径
        for(int i = 0; i < MAX; i++) {
            int move = rand() % 2;  // 随机决定弹珠的移动方向
            // 更新弹珠的位置，确保不会超出边界
            index = (move == 0 && index > 0) ? index - 1 : index + move;
            printf("%s ", move == 0 ? "左" : "右");  // 打印出弹珠的移动方向
        }

        // 弹珠最终落在哪个位置，就赢得该位置的奖品
        printf("\n恭喜你，赢得了%s！\n\n", prizes[triangle[MAX-1][index]]);
    }

    return 0;
}

五、弹珠抽奖游戏与杨辉三角的关系

        弹珠抽奖游戏与杨辉三角的关系在于它们都涉及了决策路径的选择。弹珠在下落过程中每到达一个分叉点就需要做出选择，就像在杨辉三角中从顶部走到底部，也需要在每个节点选择向左还是向右。而且，二者都能够很好地模拟和演示二项分布的特性。

六、总结

       经过对弹珠抽奖游戏与杨辉三角的深度解析，我们可以看出，虽然它们看起来大相径庭，但实际上它们有许多的相似之处。这是因为它们都可以被视为二项分布的实例。一个理性且充满感情的讨论将引导我们走向理解，理解将引导我们走向实践，而实践将带给我们卓越的编程技能。在这个美丽的计算世界中，只有当理论碰撞实践时，我们的思维才能迸发出最炫丽的火花。

附：联合应用

        我们知道，在没有其他外力作用的情况下，物体在Y轴方向上的位移可以使用公式                   y = -g * t^2 / 2 + v * t + s   来表示，其中 g 代表重力加速度，v 代表初速度，s 代表初始高度，t 代表时间。

        请注意，我们使用抛物线运动的模型来近似实际运动，具体的实际模型可能并非完全符合抛物线模型。

#include <stdio.h>

// 定义重力加速度
#define G 9.8

// 物体的初始高度和速度
double initialHeight = 100.0;
double initialSpeed = 20.0;

// 时间间隔和总时间
double timeInterval = 0.01;
double totalTime = 0.01;

int main() {
    int i;
    int numSteps = totalTime / timeInterval;

    for(i = 0; i <= numSteps; i++) {
        // 计算当前时间
        double t = i * timeInterval;

        // 计算当前位移
        double y = -0.5 * G * t * t + initialSpeed * t + initialHeight;

        printf("在时刻 %f秒, 物体位于高度为%f米的位置\n", t, y);
    }

    return 0;
}

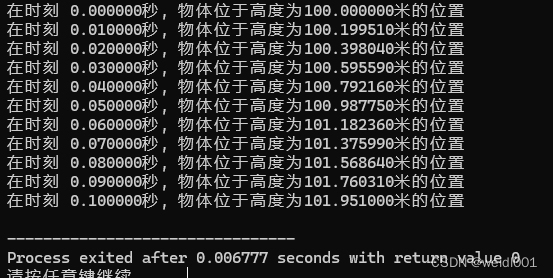
        在这个程序中，物体从100米高，向上以20米/秒的速率抛出，然后我们计算从0秒到10秒每0.01秒物体的高度。程序将每个时间步长下物体的高度打印出来，可以清楚地看到物体高度的变化，模拟了抛物线运动的过程。

如果想要计算更精确的抛物线运动，可以这样修改

#include <stdio.h>

#define G 9.8
double initialHeight = 100.0;
double initialSpeed = 20.0;
double timeInterval = 0.001;
double totalTime = 0.02;

double calculateHeight(double t, double h, double v) {
    return -0.5 * G * t * t + v * t + h;
}

void rungeKutta() {
    double t = 0; // initial time
    double h = initialHeight; // initial height
    double v = initialSpeed; // initial speed

    int numSteps = totalTime / timeInterval;
    for(int i = 0; i <= numSteps; i++) {
        double k1_y = calculateHeight(t, h, v);
        double k2_y = calculateHeight(t + timeInterval / 2, h + timeInterval * k1_y / 2, v);
        double k3_y = calculateHeight(t + timeInterval / 2, h + timeInterval * k2_y / 2, v);
        double k4_y = calculateHeight(t + timeInterval, h + timeInterval * k3_y, v);

        // Update next value of y
        h = h + (1.0 / 6.0) * timeInterval * (k1_y + 2 * k2_y + 2 * k3_y + k4_y);

        t = t + timeInterval;

        printf("在时刻 %f秒, 物体位于高度为%f米的位置\n", t, h);
    }
}   

int main() {
    rungeKutta();
    return 0;
}

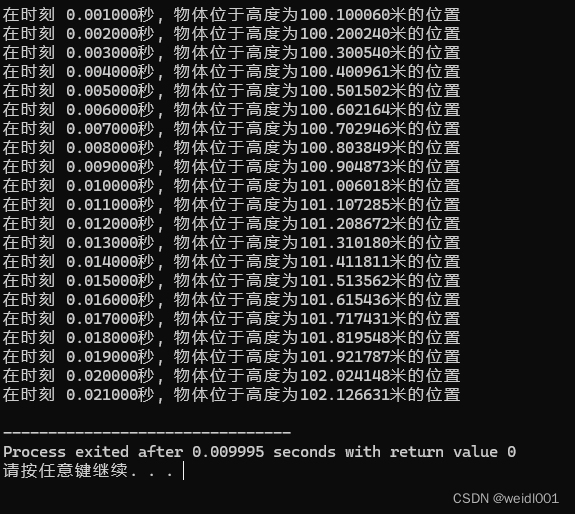
        这段程序利用了四阶龙格-库塔方法，它通过取多个斜率的平均值而不仅仅是一个斜率，可以更精准地逼近实际的微分方程的解，所以可以提高算法的准确性。

        然而，这个程序仍然只考虑了抛物线运动，没有考虑如空气阻力、物体的形状和旋转等复杂的物理因素。如果想要进行更真实的模拟，我们可能需要考虑这些更复杂的物理因素，但它们会大大提高模型和算法的复杂性。