引言

在大数据和人工智能的时代，概率论已成为数据科学和编程的核心工具。通过编程，我们能够模拟复杂的随机过程、实现统计模型，并通过数据分析来预测和决策。本文将探讨概率论与编程的交互，并展示如何通过编程来实现概率模型和算法。

---

第一章 概率模拟与编程实现

1.1 随机数生成与蒙特卡罗模拟

1.1.1 随机数生成

随机数生成是概率模拟的基础。大多数编程语言（如Python, R）都提供了生成均匀分布、正态分布等常见分布的随机数函数。通过随机数，可以模拟各种概率事件，如掷骰子、抽牌等。

编程示例：

在Python中使用NumPy库生成正态分布的随机数：

import numpy as np

# 生成1000个均值为0，标准差为1的正态分布随机数
random_numbers = np.random.normal(0, 1, 1000)

1.1.2 蒙特卡罗模拟

蒙特卡罗模拟是一种通过随机数来近似解决复杂问题的数值方法，广泛用于积分估计、风险评估和系统仿真等领域。

应用示例：

利用蒙特卡罗模拟估计圆周率 π\piπ。在单位正方形中随机投点，统计落在单位圆内的点数比例来估计 π。

import numpy as np

def estimate_pi(num_samples):
    count_inside_circle = 0
    for _ in range(num_samples):
        x, y = np.random.uniform(-1, 1, 2)
        if x**2 + y**2 <= 1:
            count_inside_circle += 1
    return (count_inside_circle / num_samples) * 4

# 估计 π 的值
pi_estimate = estimate_pi(100000)
print(f"Estimated value of π: {pi_estimate}")

应用场景：

• 金融风险分析：通过蒙特卡罗模拟评估投资组合的风险。
• 物理学：在复杂系统中近似求解多维积分。

---

第二章 统计建模与数据分析

2.1 统计模型实现

编程使得复杂的统计模型可以被轻松实现并应用于实际数据。常用的统计建模技术包括回归分析、分类模型、时间序列分析等。

2.1.1 回归分析

使用Python的Scikit-learn库实现线性回归模型，对数据进行拟合并预测。

from sklearn.linear_model import LinearRegression
import numpy as np

# 假设有一些数据点
X = np.array([[1], [2], [3], [4], [5]])
y = np.array([1, 2, 1.3, 3.75, 2.25])

# 创建并拟合模型
model = LinearRegression().fit(X, y)

# 预测
predictions = model.predict(X)
print(f"Predictions: {predictions}")

2.1.2 时间序列分析

时间序列数据常见于金融、气象、销售等领域。通过ARIMA模型等对时间序列进行分析和预测。

import pandas as pd
from statsmodels.tsa.arima.model import ARIMA

# 示例时间序列数据
data = pd.Series([100, 102, 101, 104, 108, 110, 107])

# 构建并拟合ARIMA模型
model = ARIMA(data, order=(1, 1, 1))
fit_model = model.fit()

# 预测未来值
forecast = fit_model.forecast(steps=3)
print(f"Forecast: {forecast}")

实际应用：

• 经济预测：预测未来的经济指标如GDP增长率、失业率。
• 电力负荷预测：电力公司通过时间序列分析预测未来的电力需求。

2.2 概率图模型

2.2.1 贝叶斯网络

贝叶斯网络是描述随机变量及其条件依赖关系的有向无环图。它用于概率推断和决策分析。

实现贝叶斯网络：

通过Python的pomegranate库来构建贝叶斯网络，进行推断。

from pomegranate import *

# 定义网络结构
cloudy = DiscreteDistribution({'T': 0.5, 'F': 0.5})
sprinkler = ConditionalProbabilityTable(
    [['T', 'T', 0.1], ['T', 'F', 0.9],
     ['F', 'T', 0.5], ['F', 'F', 0.5]], [cloudy])
rain = ConditionalProbabilityTable(
    [['T', 'T', 0.8], ['T', 'F', 0.2],
     ['F', 'T', 0.2], ['F', 'F', 0.8]], [cloudy])
wet_grass = ConditionalProbabilityTable(
    [['T', 'T', 'T', 0.99], ['T', 'T', 'F', 0.01],
     ['T', 'F', 'T', 0.9], ['T', 'F', 'F', 0.1],
     ['F', 'T', 'T', 0.9], ['F', 'T', 'F', 0.1],
     ['F', 'F', 'T', 0.0], ['F', 'F', 'F', 1.0]], [sprinkler, rain])

# 构建模型
s1 = State(cloudy, name="cloudy")
s2 = State(sprinkler, name="sprinkler")
s3 = State(rain, name="rain")
s4 = State(wet_grass, name="wet_grass")

network = BayesianNetwork("Rain Problem")
network.add_states(s1, s2, s3, s4)
network.add_edge(s1, s2)
network.add_edge(s1, s3)
network.add_edge(s2, s4)
network.add_edge(s3, s4)
network.bake()

# 推断
beliefs = network.predict_proba({'wet_grass': 'T'})
print(f"Probability distribution: {beliefs}")

应用场景：

• 医学诊断：根据症状推断疾病概率。
• 机器学习：用于特征选择和建模复杂系统中的变量依赖关系。

---

第三章 概率论在机器学习中的应用

3.1 随机森林与决策树

随机森林是一种集成学习方法，基于多个决策树的投票结果进行预测，具有高精度和抗过拟合能力。它依赖于概率分布的采样技术，如Bootstrap。

3.1.1 决策树与信息熵

决策树通过信息熵（entropy）来选择最佳分割点。信息熵衡量随机变量的不确定性，定义为：

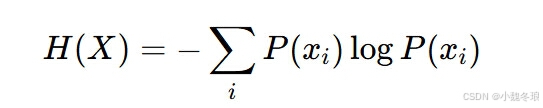
实现随机森林：

from sklearn.ensemble import RandomForestClassifier
from sklearn.datasets import load_iris
from sklearn.model_selection import train_test_split

# 加载数据集
iris = load_iris()
X, y = iris.data, iris.target

# 划分训练集和测试集
X_train, X_test, y_train, y_test = train_test_split(X, y, test_size=0.3)

# 创建并训练模型
model = RandomForestClassifier(n_estimators=100)
model.fit(X_train, y_train)

# 预测与评估
accuracy = model.score(X_test, y_test)
print(f"Model Accuracy: {accuracy}")

应用场景：

• 金融信用评分：通过随机森林评估借款人信用风险。
• 生物信息学：用于基因表达数据的分类分析。

3.2 贝叶斯分类器

贝叶斯分类器是基于贝叶斯定理的分类模型，通常用于文本分类、图像识别等任务。朴素贝叶斯假设特征之间相互独立，简化了计算。

实现朴素贝叶斯分类器：

from sklearn.naive_bayes import GaussianNB
from sklearn.metrics import accuracy_score

# 创建并训练模型
model = GaussianNB()
model.fit(X_train, y_train)

# 预测
predictions = model.predict(X_test)

# 评估模型
accuracy = accuracy_score(y_test, predictions)
print(f"Naive Bayes Model Accuracy: {accuracy}")

应用实例：

• 垃圾邮件过滤：基于词频和邮件内容的概率分布判断邮件是否为垃圾邮件。
• 情感分析：分析文本的情感倾向，如正面或负面评价。

---

总结与展望

通过编程实现概率论模型，我们不仅能够更好地理解理论，还能在数据分析、机器学习等领域中灵活应用这些工具。这些应用不仅限于理论研究，还能为实际问题提供有效的解决方案。随着计算能力的提升和大数据的普及，概率论与编程的结合将继续推动各行业的创新发展。