问题

请你设计一个 最小栈 。它提供 push ，pop ，top 操作，并能在常数时间内检索到最小元素的栈。

实现 MinStack 类:

• MinStack() 初始化堆栈对象。
• void push(int val) 将元素val推入堆栈。
• void pop() 删除堆栈顶部的元素。
• int top() 获取堆栈顶部的元素。
• int getMin() 获取堆栈中的最小元素。

示例 

输入：
["MinStack","push","push","push","getMin","pop","top","getMin"]
[[],[-2],[2],[-3],[],[],[],[]]

输出：
[null,null,null,null,-3,null,2,-2]

解释：
MinStack minStack = new MinStack();
minStack.push(-2);
minStack.push(2);
minStack.push(-3);
minStack.getMin();   --> 返回 -3.
minStack.pop();
();      --> 返回 2.
minStack.getMin();   --> 返回 -2.

分析

本题目的难点在于，出了要实现间的栈操作，还得满足在常数时间内找到最小值。因此时间成本要求极高。所以不能进行数据的遍历去找到合适的数值。

因此，我们可以考虑空间换时间的方法。用额外开辟的空间，去换得最小的时间消耗。

思路

我们可以建立两个stack，第一个叫st，用来正常出入数据；第二个叫minst，将最小的数入到该栈。

示例：

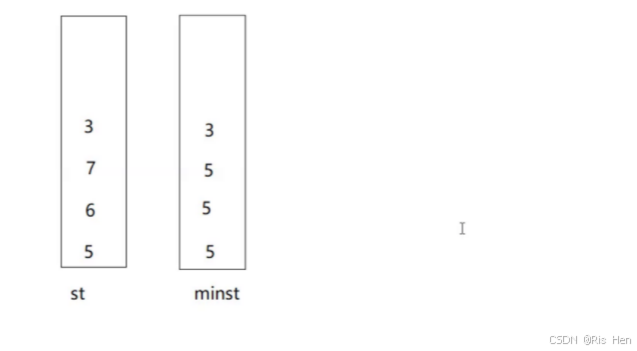
当我们打算入5 6 7 3时， st作为正常栈，存储5 6 7 3。

当5入栈时，minst为空，5入minst-------->当6 7入栈时，6  7均大于5（minst栈顶），因此入5（保证minst的栈顶始终是最小值）---------->当3入栈时，3小于等于()，因此3入minst。

（需要注意，当插入的元素 x 等于 ()时，仍需要插入）

优化：

为了减少入栈的消耗，在minst中“当6 7入栈时，6  7均大于5（minst栈顶），因此入5（保证minst的栈顶始终是最小值）”此操作省去

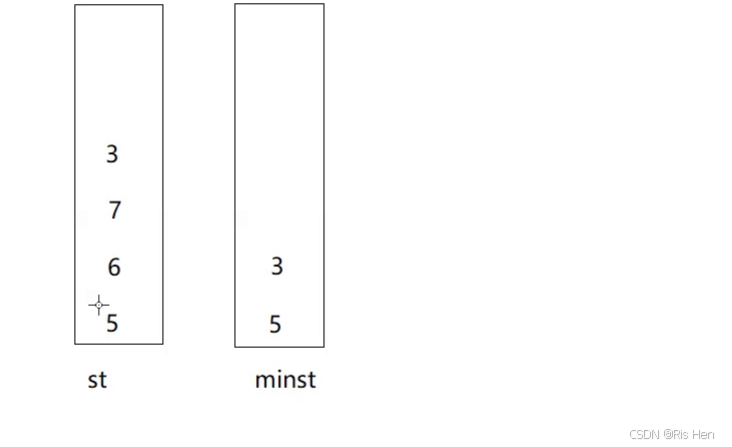
因此在需要满足的push、top、pop操作如下：

top：

返回st栈的栈顶

push：

st栈优先插入，当插入的数据x小于等于（）时，minst才插入x

pop：

st栈优先删除，当删除的数据等于（）时，minst才删除。（（因为（）始终小于等于（）   ））

代码实现

class MinStack {
public:
    MinStack() {    //不写，在初始化列表自动完成初始化
    }
    
    void push(int x) {
        _st.push(x);

        if (_minst.empty() || x <=  _())
            _minst.push(x);
    }
    
    void pop() {

        if (_() == _())
            _minst.pop();

        _st.pop();

    }
    
    int top() {
        return _();
    }
    
    int getMin() {
        return _();
    }

private:
    stack<int> _st;
    stack<int> _minst;

};

题外话

当出现大量重复元素时，minst还需要大量的push这些重复元素吗？

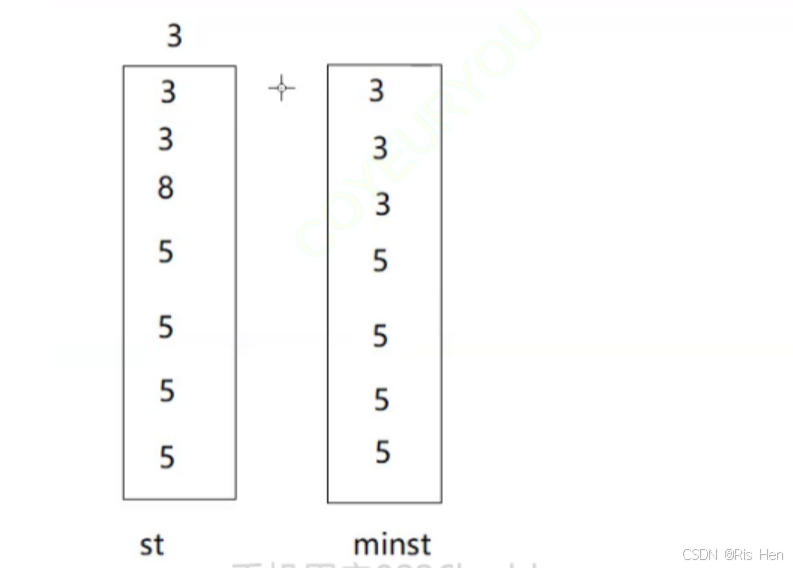
答案是不需要。我们只需要将minst初始化为一个自定义类型即可。

采用类内初始化，建立一个这样的类。当传入相同的元素时，只需要_count++即可。