附有过程详细思路图解，最后有整体实现的代码

一、堆排序

堆排序是利用堆这种数据结构而设计的一种排序算法，堆排序是一种选择排序，它的最坏，最好，平均时间复杂度均为O(nlogn)，它是不稳定排序。

1.堆排序简介

堆是一个近似完全二叉树（可以简单理解为从根到最后一层，只有最后一层可以存在二叉树的深度为h，除第 h 层外，其它各层 (1～h-1) 的结点数都达到最大个数，第 h 层所有的结点都连续集中在最左边）的结构，并同时满足堆积的性质：即子结点的键值或索引总是小于（或者大于）它的父节点。

所以堆排序可以有两种：
大顶堆：每个结点的值都大于或等于其左右孩子结点的值；
小顶堆：每个结点的值都小于或等于其左右孩子结点的值。

这里有一个动态可以看一下加强理解，如果不理解也不影响，继续看下去

2.算法思路
这里我是建造大顶堆，利用将数组放入树中，并借助队列记录左右子树的父亲节点，这样方便将数组中的数放入树中节点，可以满足完全二叉树的特点

下面结合图来举例解释
例如，我们有数组{10，8，7，6，5，4，2}
（1） 将第一个10放入树中的同时，同时也让10进入队列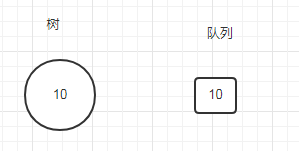

（2） 然后按照从左到右的顺序给10安排孩子，让8和7分别作为10的左右孩子放进树中，同时也进入队列，10可以出队了

（3） 同理给8安排孩子，分别是6和5，同时也记录到队列中，8也不需要了那就出队

（4） 利用队列的重点来了，当我们将数组中的5放入到8的右孩子后，如何将4快速定位到7的左孩子呢，这个时候我们只要去找队头的7，就解决问题了。

这样的树就是我们要构建的完全二叉树了，因为举例比较特殊，所以直接也是大顶堆了

3.代码实现

 //整体思路，将数组中的数变为堆排序，
    // 借助队列记录左右子树的父亲节点，方便放入树中节点（画图解释）
    public static void creatTree(int a[]) {//创建完全二叉树
        LinkedList<treeNode> listNode = new LinkedList();//新建链表，链表模拟队列
        treeNode root = new treeNode(a[0]);//将数组第一位记录到根节点
        listNode.addFirst(root);//将根节点数值入队
        int temp;//声明借助temp进行两数的交换
        for(int i=1;i<a.length;i++) {//for循环遍历数组放入树中（真正的建树过程），以下注释以第一遍循环为例
            treeNode thisNode = listNode.getFirst();//将队列中第一个放入树的第一个节点对象（第一次循环为根节点）
            if (thisNode.getLeft() == null) {  //左孩子为空的情况下
                treeNode newNode = new treeNode(a[i]);//新建节点存放数组第二个值
                listNode.add(newNode);//队列中增加此时的第二个值
                thisNode.setLeft(newNode);//first节点连接左孩子
                newNode.setParent(thisNode);//左孩子连接父亲节点
                while (newNode.value>thisNode.value){//为了构建大顶堆，插入节点的值与父亲节点值进行比较，保证父亲节点值大
                    temp=newNode.value;
                    newNode.value=thisNode.value;
                    thisNode.value=temp;
                    if(thisNode==root){//根节点无父亲节点
                        break;
                    }
                    newNode = thisNode;//保证所有的孩子节点和父亲节点遵循大顶堆原则（父亲节点值大于孩子节点）
                    thisNode=thisNode.getParent();
                }
            }
            else if(thisNode.getRight()==null){//右子树同上
                treeNode newNode = new treeNode(a[i]);
                listNode.add(newNode);
                thisNode.setRight(newNode);
                newNode.setParent(thisNode);
                listNode.removeFirst();
                while (newNode.value>thisNode.value){
                    temp=newNode.value;
                    newNode.value=thisNode.value;
                    thisNode.value=temp;
                    if(thisNode==root){
                        break;
                    }
                    newNode = thisNode;
                    thisNode=thisNode.getParent();
                }
            }
        }

一个大顶堆的逻辑就这么出来了，下面看看广度优先遍历

---

二、二叉树的广度优先遍历

1. 二叉树的广度优先遍历介绍
这是百度百科解释：广度优先遍历
我们可以将二叉树的广度优先遍历理解为：对二叉树整体进行从上到下，每层从左到右的遍历。
2.算法思路
对于二叉树的广度优先遍历的做法类似上面构建大顶堆。

利用队列记录操作的父亲，并将其左右孩子存入队列，只是这是不将父亲出队，而是利用标记来指引树的节点在队列中的索引。最后的队列输出结果就是广度优先遍历结果。
继续用图来解释：
（1） 首先把根节点10放入队列，并用红色代表我们标记的索引

（2） 如果10的左孩子不为空，我们把8放入队列，右孩子也不空，7也放入队列，10的左右孩子都遍历了，但是这是我们不将10出队，只是将标记下移到8

（3） 利用队列加标记的重点在这里：下面我们该遍历8的左右孩子了，如果8的左孩子不为空，将6入队，右孩子不为空，5入队，8的左右孩子遍历完了，同样是将标记下移到7，目的也是为了方便直接定位到7的左右孩子，进行遍历

（4） 后面依次类推
3.代码实现

//通过队列按照每一层树从左到右输出
        LinkedList<treeNode> queue = new LinkedList(); //链表模拟队列
        int flag = 0;//用来标记树的节点在队列中的索引
        queue.add(root);//根节点加入队列头
        treeNode rroot ;//操作节点的父亲
        while(queue.size()!=a.length){
            rroot = queue.get(flag++);
            if(rroot.getLeft() != null){//左孩子不空，放入队列
                queue.addLast(rroot.getLeft());
            }
            if(rroot.getRight() !=null){//右孩子不空，放入队列
                queue.addLast(rroot.getRight());
            }
        }
        for(int i = 0;i<queue.size();i++){//队列先进先出的性质输出
            System.out.print(queue.get(i).value+"  ");
        }

---

三、Java实现大顶堆和二叉树的广度优先遍历全部代码及注释详解
下面就是将堆排序和广度优先遍历结合起来了直接上代码，有两个文件

Tree.java

import java.util.LinkedList;
public class Tree {
    //整体思路，将数组中的数变为堆排序，
    // 借助队列记录左右子树的父亲节点，方便放入树中节点（画图解释）
    public static void creatTree(int a[]){//创建完全二叉树
        LinkedList<treeNode> listNode = new LinkedList();//新建链表，链表模拟队列
        treeNode root = new treeNode(a[0]);//将数组第一位记录到根节点
        listNode.addFirst(root);//将根节点数值入队
        int temp;//声明借助temp进行两数的交换
        
        for(int i=1;i<a.length;i++) {//for循环遍历数组放入树中（真正的建树过程），以下注释以第一遍循环为例
            treeNode thisNode = listNode.getFirst();//将队列中第一个放入树的第一个节点对象（第一次循环为根节点）
            if (thisNode.getLeft() == null) {  //左孩子为空的情况下
                treeNode newNode = new treeNode(a[i]);//新建节点存放数组第二个值
                listNode.add(newNode);//队列中增加此时的第二个值
                thisNode.setLeft(newNode);//first节点连接左孩子
                newNode.setParent(thisNode);//左孩子连接父亲节点
                while (newNode.value>thisNode.value){//为了构建大顶堆，插入节点的值与父亲节点值进行比较，保证父亲节点值大
                    temp=newNode.value;
                    newNode.value=thisNode.value;
                    thisNode.value=temp;
                    if(thisNode==root){//根节点无父亲节点
                        break;
                    }
                    newNode = thisNode;//保证所有的孩子节点和父亲节点遵循大顶堆原则（父亲节点值大于孩子节点）
                    thisNode=thisNode.getParent();
                }
            }
            else if(thisNode.getRight()==null){//右子树同上
                treeNode newNode = new treeNode(a[i]);
                listNode.add(newNode);
                thisNode.setRight(newNode);
                newNode.setParent(thisNode);
                listNode.removeFirst();
                while (newNode.value>thisNode.value){
                    temp=newNode.value;
                    newNode.value=thisNode.value;
                    thisNode.value=temp;
                    if(thisNode==root){
                        break;
                    }
                    newNode = thisNode;
                    thisNode=thisNode.getParent();
                }
            }
        }
        //通过队列按照每一层树从左到右输出大顶堆
        LinkedList<treeNode> queue = new LinkedList(); //链表模拟队列
        int flag = 0;//用来标记树的节点在队列中的索引
        queue.add(root);//根节点加入队列头
        treeNode rroot ;//操作节点的父亲
        while(queue.size()!=a.length){
            rroot = queue.get(flag++);
            if(rroot.getLeft() != null){//左孩子不空，放入队列
                queue.addLast(rroot.getLeft());
            }
            if(rroot.getRight() !=null){//右孩子不空，放入队列
                queue.addLast(rroot.getRight());
            }
        }
        for(int i = 0;i<queue.size();i++){//队列先进先出的性质输出
            System.out.print(queue.get(i).value+"  ");
        }
    }
    public static void main(String[] args) {
        int a[] = {11,10,4,43,34,54,6};
        creatTree(a);
    }
}

treeNode.java

public class treeNode {
    private treeNode left;
    private treeNode right;
    private treeNode parent;
    int value;

    public treeNode getLeft() {
        return left;
    }
    public void setLeft(treeNode left) {
        this.left = left;
    }
    public treeNode getRight() {
        return right;
    }
    public void setRight(treeNode right) {
        this.right = right;
    }
    public int getValue() {
        return value;
    }
    public void setValue(int value) {
        this.value = value;
    }
    public treeNode getParent() {
        return parent;
    }
    public void setParent(treeNode parent) {
        this.parent = parent;
    }
    public treeNode(int value){
        this.value = value;
    }
}

写着是排序，实际就是构造完大顶堆后对其进行取最大值就好。