字符串
- 代码随想录
-
如果想让这套题目有意义,就不要申请额外空间。
344.反转字符串
- 双指针
// 时间复杂度O(n),执行n/2次交换
// 空间复杂度O(1)
class Solution {
public:
void reverseString(vector<char>& s) {
int n = s.size();
for(int left = 0,right = n-1;left <= right;left++,right--){
swap(s[left],s[right]);
}
}
};
541. 反转字符串II
- 分情况讨论,其实除去剩余字符数量小于k个,将剩余全部反转;
- 大于k个小于2k,与正常反转2k个中的前k个,是相同的(即i+k <= n),都是反转该子串中的前k个。
// 时间复杂度 O(n)
// 空间复杂度 o(1)-字符串
class Solution {
public:
string reverseStr(string s, int k) {
int n = s.size();
// 先进入循环,然后判断剩余的数量,再分情况讨论。
for(int i = 0 ;i < n;i+=2*k){
if(i + k < n){
// 剩余字符大于k小于2k,其实这种情况就与正常的剩余2k个字符一样,反转当前字符该k个字符
// 反转2k个字符的前k个字符
reverse(s.begin()+i,s.begin()+i+k);
}else{
// 剩余字符小于k个,反转剩余所有字符
reverse(s.begin()+i,s.end());
}
}
return s;
}
};
- 自己实现reverse
- 注意区间控制
// 时间复杂读O(n)
// 空间复杂度O(1)
class Solution {
public:
void myReverse(int begin,int end,string& s){
// 左闭右闭
for(int l = begin,r = end;l <= r;l++,r--){
swap(s[l],s[r]);
}
}
string reverseStr(string s, int k) {
int n = s.size();
for(int i = 0;i < n;i += 2*k){
if(i + k < n){
myReverse(i,i+k-1,s);// 右边界i+k-1
}else{
myReverse(i,n-1,s);
}
}
return s;
}
};
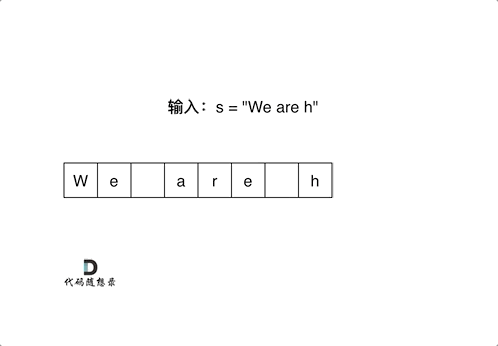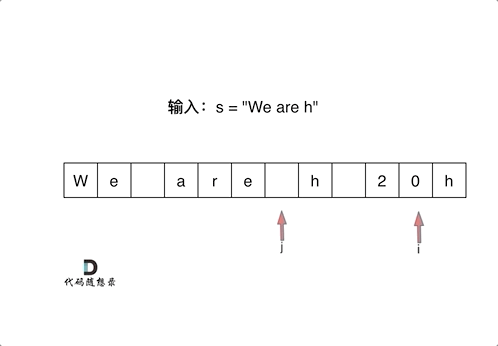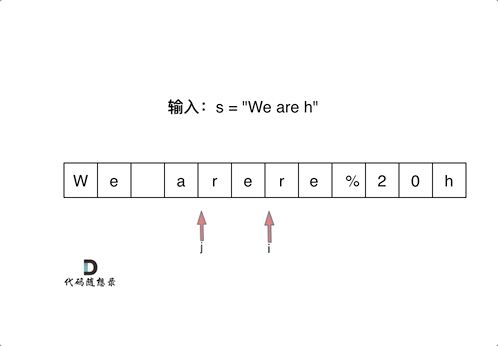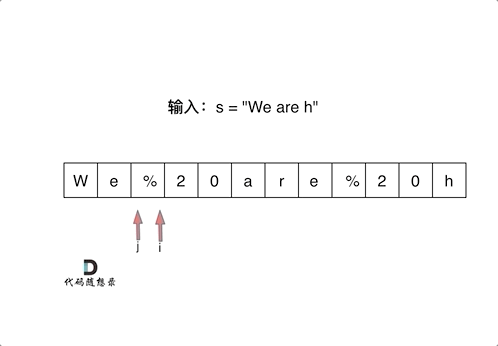
剑指Offer 05.替换空格
- 搜寻空格个数,扩充数组,起两个指针,从后向前遍历,一个指针(慢)指向新开辟数组的最后一个位置,一个指针(快)指向旧数组大小的位置。
- 快指针不为空格,与慢指针交换到最后,反之使用慢指针填充%20。
- 要是用快指针填充,就覆盖前面还没判断的了。
- 填充过程如下图所示:
- 如果从前往后填充,就变成O(n²)的算法了,因为每次添加元素过后都要将后面的元素往后移动。
-
很多数组填充类问题,都可以预先给数组扩容为填充后的大小,然后再从后向前进行操作
- 这么做有两个好处:
- 不用申请新数组
- 从后向前填充元素,避免从前往后填充导致的元素向后移动。
// 时间复杂度 O(n)
// 空间复杂度 O(1)
class Solution {
public:
string replaceSpace(string s) {
int oldSize = s.size();
int count = 0;
for(char& c:s){
if(c == ' ')count++;
}
s.resize(oldSize+2*count);// 注意是2,因为原来的空格是占一个,所以每个空格再扩充2个即可
int newSize = s.size();
for(int slow = newSize-1,fast = oldSize-1;fast < slow;slow--,fast--){
if(s[fast] != ' '){
s[slow] = s[fast];
}else{
s[slow] = '0';
s[slow-1] = '2';
s[slow-2] = '%';
slow -= 2;
}
}
return s;
}
};
151. 反转字符串中的单词
- 空间复杂度O(1)实现思路:
- 去掉多余空格,重新添加空格。
- 整体反转
- 遍历,以单词为整体再次反转。
// 时间复杂度O(n)
// 空间复杂度O(1)
class Solution {
public:
// 反转左闭右闭区间
void myReverse(string& s,int start,int end){
for(int i = start,j = end; i < j;i++,j--){
swap(s[i],s[j]);
}
}
// 去掉多余空格——不能这么删除,这么删,一个空格都不留了
// void removeExSpace(string& s){
// int n = s.size();
// int slow = 0;
// for(int fast = 0;fast < n; fast++){
// if(s[fast] != ' '){
// s[slow++] = s[fast];
// }
// }
// s.resize(slow);
// }
// 去掉多余空格,手动添加正确的空格
// 方法类似于24.移除元素-快慢指针
void removeExSpace(string& s){
int n = s.size();
int slow = 0;
for(int fast = 0; fast < n;fast++){
if(s[fast] != ' '){
if(slow != 0)s[slow++]=' ';//注意是slow,除去第一个单词,在每个单词的前面添加空格。
// 边界控制 fast < n
while(fast < n && s[fast] != ' '){
s[slow++] = s[fast++];
}
}
}
// slow最后停在最后一个字符后,即元素个数。
s.resize(slow);
}
string reverseWords(string s) {
removeExSpace(s);// 去掉多余空格
int n = s.size();
myReverse(s,0,n-1);// 整体反转
// 遍历,按照空格反转每个单词
int slow = 0;
// 注意边界控制,i <= n,是因为要划到最后一个单词。
for(int i = 0;i <= n;i++){
if(i == n || s[i] == ' '){// i== n的意思是反转最后一个单词
myReverse(s,slow,i-1);// 到i-1的意思是,这里是到了空格才开始反转的,前一个就是上一个单词的最后一个字母,myReverse是左闭右闭区间的。
slow = i+1;
}
}
return s;
}
};
- 分开删除前面、中间、后面,多余空格的方法如下所示:
- 双指针删除,O(n)时间复杂度
void removeExSpaceII(string& s){
// 先删除头部多余的空格
int fast = 0;
int slow = 0;
int n = s.size();
while(n > 0 && fast < n && s[fast] == ' ')fast++;
// 删除中间的多余空格
for(;fast < n;fast++) {
if (fast > 0 && s[fast] == s[fast - 1] && s[fast] == ' ') {// 出现多个空格
continue;
} else {
s[slow++] = s[fast];
}
}
// 删除最后的多余空格
if(slow-1 > 0 && s[slow] == ' '){
s.resize(slow-1);
}else{
s.resize(slow);
}
}
剑指Offer58-II.左旋转字符串
- 不申请额外空间,有趣的做法, 如下图所示:

// 时间复杂度O(n)
// 空间复杂度O(1)
class Solution {
public:
string reverseLeftWords(string s, int n) {
reverse(s.begin(),s.begin()+n);
reverse(s.begin()+n,s.end());
reverse(s.begin(),s.end());
return s;
}
};
- 申请额外空间,substr拼接
class Solution {
public:
string reverseLeftWords(string s, int n) {
int _Size = s.size();
string front = s.substr(0,n);
string back = s.substr(n,_Size-n);
return back+front;
}
};
28. 找出字符串中第一个匹配项的下标
- 暴力算法
// 时间复杂度O(n²)
class Solution {
public:
int strStr(string haystack, string needle) {
int hs = haystack.size();
int ns = needle.size();
for(int i = 0; i < hs;i++){
int tmp = i;// 保存开始匹配i的位置
for(int j = 0;j < ns;j++){
if(haystack[i] != needle[j]){
i = tmp;// 将i重置回去
break;
}else{
if(j == ns-1)return tmp;// 相等并且已经到达结尾模式串结尾
i++;// 继续走
}
}
}
return -1;
}
};
- KMP算法
- KMP算法相关补充——【KMP】KMP算法的一些小理解&总结
- 这里仅给出代码实现,详见上述文章中。
// 时间复杂度O(n)
class Solution {
public:
void getNext(int* next,const string s){
int n = s.size();
int j = 0;
next[0] = 0;
// i 为前缀末尾
// j 为后缀末尾
for(int i = 1; i < n ;i++){
while(j > 0 && s[i] != s[j]){// 控制回退,最多回退到开头,即j=0
j = next[j-1];
}
if(s[i] == s[j])j++;
next[i] = j;
}
}
int strStr(string haystack, string needle) {
int next[needle.size()];
// j负责遍历模式串
// i负责遍历文本串
getNext(next,needle);
int j = 0;
for(int i = 0;i < haystack.size();i++){
// 当前这个字符不同,通过移动j指针指向的模式串位置,来调整继续匹配的位置。
while(j > 0 && haystack[i] != needle[j]){
j = next[j-1];
}
if(haystack[i] == needle[j])j++;
if(j == needle.size()){
return i-needle.size()+1;
}
}
return -1;
}
};
459. 重复的子字符串
- 移动匹配
// 时间复杂度 O(n),不确定
class Solution {
public:
bool repeatedSubstringPattern(string s) {
string t = s + s;
// 掐头去尾
t.erase(t.begin());
t.erase(t.end()-1);// 注意end指向最后一个元素后
return t.find(s)!=string::npos?true:false;
}
};
- KMP算法
- 详情也请见上题所给出的KMP相关文章链接。
// 时间复杂度O(n)
class Solution {
public:
void getNext(int* next,const string& s){
int j = 0;
next[0] = 0;
for(int i =1; i < s.size();i++){
while(j > 0 && s[i] != s[j]){
j = next[j-1];
}
if(s[i] == s[j])j++;
next[i] = j;
}
}
bool repeatedSubstringPattern(string s) {
if(s.size() == 0)return false;
int next[s.size()];
getNext(next,s);
int len = s.size();
// next[len-1] == 0就说明,以整体为子串的最长相等前后缀为0。
// 如果是通过某一字串重复得到的,以整体为子串的最长相等前后缀不会为0。
// 最小重复单位如果能被字符串的长度整除,说明该字符串是由重复的子串构成的。
if(next[len-1] != 0 && len % (len-(next[len-1])) == 0)return true;
return false;
}
};

