无论是不是数据库行业的从业者，但凡对数据库有所了解的人都知道所谓“优化器是数据库的大脑”这样的说法。查询优化器（Optimizer）是数据库内核开发的重点和难点，也是数据库查询性能的关键点。优化器生成的不同执行计划的性能可能会有数量级别的差异，所以查询优化能力很大程度上决定了数据库的性能。随着数据库进入分布式时代，分布式的查询优化更加剧了优化的难度。优化器的三要素中搜索空间和代价模型在分布式场景下都面临了全新的挑战，与之相应的搜索策略也有了新的研究。

搜索空间

    单机数据库优化器的搜索空间主要体现在数据访问方法、连接方法和连接顺序三个方面，其他因素对搜索空间的影响不大。在分布式的场景中，连接方法的搜索除了要考虑单机实现之外，还需要考虑其分布式的实现。例如单机场景中，连接的实现方法通常有hash join、merge join 和 nested loop join三种。而到了分布式场景，通常的实现方法会有partitioned wise join、partitial partitioned wise join、rehash distribution join 和 broadcast distribution join等。分布式的实现方法导致计划树在层级上增加，每增加一层就可以以正交下层计划节点的形式扩大计划搜索空间，呈指数膨胀。

    除了连接方法增加导致搜索空间的膨胀，分布式场景下连接顺序也会引起搜索空间扩大。因为在分布式场景里，不仅计划节点类型增多，同时也需要保留更多的物理属性从而导致了更大的计划搜索空间。在单机系统中，候选路径除了考虑其cost之外，往往需要考虑其序（ordering）属性。一个候选路径如果带有对未来上层算子可能有用的序属性，即便其代价更大，也需要被保留。到了分布式场景里，仅仅序属性不足以表达一个路径的物理属性，分布信息同样影响上层计划的选择。分布信息主要包括分布键、分布算法和物理位置等信息。分布信息从根本上决定了分布式算子的选择，比如一个连接选择 partitioned wise join 还是rehash distribution join直接取决于分区信息。一个候选路径可能没有有用的序属性、代价也相对更高，但是如果其具有有用的分布信息，这样的路径同样需要被保留。所以在分布式查询优化中，除了维护序这个物理属性之外，还需要维护分布信息这个物理属性。多了一个维度的物理信息，最终会影响计划裁剪和计划选择，优化器更有可能选中更优的计划。但是同时也增加了分布式查询优化器的搜索空间。

代价模型

    现代CBO利用代价衡量一个执行计划的执行时间或者对数据库系统资源的占用量，包括 CPU 资源、IO 资源、网络资源等。单机优化器的代价模型通常只需要考虑 CPU 和 IO 代价，而在分布式系统里，数据需要在节点间传输，除了考虑 CPU 和 IO 的代价之外，还需要考虑网络传输代价。不同的分布式算子，其网络传输数据量相差很大，代价也会有很大差异。在一些OLAP场景里，甚至网络传输代价会成为代价模型的决定因素。除此之外，分布式系统特定相关的并行度、bloom filter 等的代价都需要得到准确的评估。这些因素都增加了分布式代价模型设计和拟合的复杂程度。

    除此之外，代价模型所依赖的统计信息在分布式场景里也迎来了新的挑战。统计信息一般分为系统统计信息和对象统计信息。系统统计信息衡量得数数据库系统所依赖的硬件本身的性能属性，例如CPU性能、内存大小、内存读写速度、IO带宽、IO速度等等。这些信息将在代价模型中用来评估一个查询计划的执行代价。对象统计信息就是我们所熟知的数据库对象的数据分布特征，一般包括表级统计信息，包括表和索引的行数、页面数等信息，以及列级统计信息，包括min/max、distinct、histogram等等。分布式数据库在系统统计信息和对象统计信息两方面都提出了新的问题：

• 单机系统统计信息不考虑网络性能，分布式系统的系统统计信息在CPU、内存、IO之外，还需要考虑网络特性。
• 单机系统的统计信息只考虑本机的统计信息即可，分布式系统除了需要考虑每个节点的局部统计信息之外，还需要考虑系统的全局统计信息。

二阶段分布式查询优化

    理论上完全考虑了分布式场景的完整搜索空间的话，优化器能够找到最优计划。但是在工业实现上为了使得查询优化器现实可用，在可控的时间里能够获得一个较优计划，必须尽可能缩小计划搜索空间。业界普遍采用二阶段分布式查询优化方法。

第一阶段: 使用优化器的单机查询优化能力生成一个单机最优的执行计划。

第二阶段: 基于分布式代价模型在单机计划上增加分布式算子。

    下图举一个二阶段分布式查询优化方法的例子，假设一个查询是三张表的关联：T1、T2、T3。

• 三个表都按照id列hash分布在4节点的数据库集群。
• T1和T2的连接条件为T1.a = T2.id
• T1和T3的连接条件为T1.id = T3.id

    那么在生成单机计划的时候，因为不考虑分布信息，很可能会生成T1、T2先连接，然后再和T3连接的计划，如下图左方的计划所示。在第二阶段考虑分布信息并在合适的位置嵌入分布式节点。此时会发现T1和T2的分布键和连接键不一致，必须做数据重分布，选择了对T1的a列做重分布，所以T1和T2的连接结果按照T1.a呈hash分布。此时再和T3做连接的时候，连接键又和分布键不一致，需要再次做重分布，所以T1和T2的连接结果需要按照T1.id再次重分布。计划如下图右方所示。

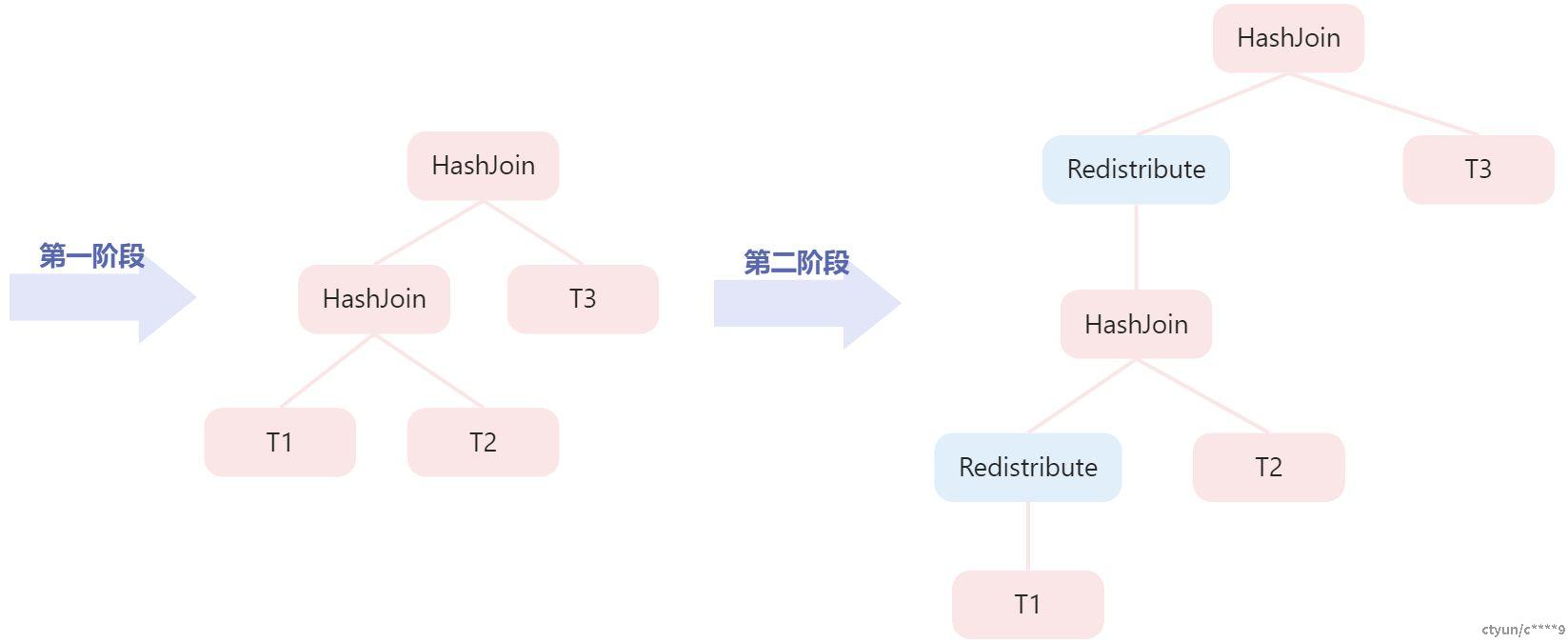
    最终生成的分布式计划的里发生了两次数据重分布。稍作分析我们就可以发现，T1原本就是按照id键呈hash分布的，为了和T2连接做了数据重分布，破坏了原本id键的分布性。为了和T3连接又重新按照id键重分布。这里的两次重分布是一个浪费。如果我们一开始就能够发现T1和T3的分布键和连接键一致可以做Partitioned wisejoin，从而让T1和T3先做连接，连接的结果按照id呈hash分布，再和T2做连接的时候只需要数据重分布一次就可以了。如下图所示。尤其是如果T1和T3的连接结果如果大幅减少的话，重分布的数据进一步减少，性能会更优。

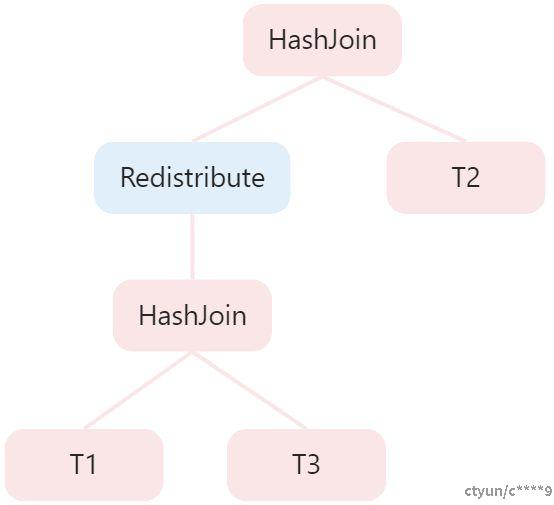
    但是因为二阶段分布式优化方法的局限性，这一候选计划在一阶段的时候就已经被抛弃了，所以二阶段不可能再生成这样的计划，从而错失了最优计划。这一局限性是为了缩小搜索空间，简化分布式查询优化复杂度引入的。上面的例子就是一个典型的因为没有考虑分布式信息导致选择了不优的连接顺序，事实上连接方法的在第一阶段的裁剪同样会造成最优计划的错失。

    例如在一阶段生成单机计划的时候，可能因为数据量较少，选择了nestloop计划，导致第二阶段选择的也是nestloop计划。而事实上在分布式系统里，如果考虑到节点数对数据量的影响，很可能nestloop并不是最优。尤其是当涉及到跨节点rescan的时候，nestloop往往会是最差的计划。

一阶段分布式查询优化

    一阶段分布式查询优化方法在生成每一步查询路径的时候都会同时枚举本地算法和分布式算法，使用分布式代价模型来评估代价每一条路径的代价，而不是通过分两个阶段分别枚举本地算法和分布式算法。同时在每个路径节点做裁剪的时候从代价、可用序、可用分布键三个维度综合考虑，保留所有对上层可能有用的路径。这种方式充分考虑了分布式对计划形状、连接方法和数据访问方法的影响，减少了提前裁剪，可以有效规避上述问题。

    仍旧以上述例子进行分析，为了简化，我们忽略掉连接算法的影响，仅考虑连接顺序中关系上的路径一个子维度。我们用一个集合的形式来描述一个关系，例如(T1, T2)描述的是T1表和T2表的连接关系。分布式查询优化器在考虑两表连接时，分别生成了以下几个候选路径：

• 路径2-1：(T1, T2)：T1按a键hash重分布，结果以T1.a键呈hash分布
• 路径2-2：(T1, T2)：T2广播数据，结果以T1.id键呈hash分布
• 路径2-3：(T1, T3)：Partitioned wise join，结果以T1.id键呈hash分布

    这三种路径分别具有不同的物理分布属性，所以三种路径都需要保留。到了三表连接阶段，生成以下路径：

• 路径3-1：((T1, T2), T3)：(T1, T2)按id键hash重分布
• 路径3-2：((T1, T2), T3)：(T1, T2)广播数据
• 路径3-3：((T1, T2), T3)：T3广播数据
• 路径3-4：((T1, T3), T2)：(T1, T2)按T1.a键hash重分布
• 路径3-5：((T1, T3), T2)：(T1, T3)广播数据
• 路径3-6：((T1, T3), T2)：T2广播数据

    到此为止已经是计划的最顶层，按照cost选择最小的即可，大概率会选中仅进行了一次数据重分布的路径3-4，而不是像两阶段优化方法，在第一阶段就因为没有考虑分布物理属性而提前丢弃中间代价较高的2-3。当然，很显然的，一阶段优化算法比二阶段算法的搜索空间大了很多，搜索时间更长。为了解决计划空间膨胀的问题，需要更多有效的手段进行对冲，比如设置更多的快速裁剪策略提前剪枝，或者在搜索策略方面采取更高效的枚举算法。