模式匹配
Kmp:
求Next数组:
若S[j+1]==S[k] :next[j+1] = k+1
若S[j+1]!=S[k] :k = next[k-1] 重复此步骤,直到next[k]==0或匹配成功为止
Kmp search:
while j > 0 and text[i] != pattern[j]:
j = next[j-1]
目标串不动 动模式串
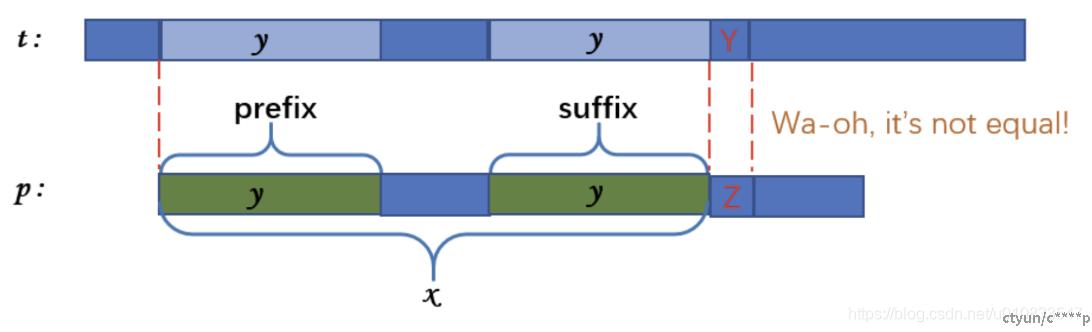
AC: Trie + Kmp
Fail指针:当前字符失配时跳转到另一段从root开始每一个字符都与当前已匹配字符段某一个后缀完全相同且长度最大的位置继续匹配
Fail指针构建:
沿着它父亲节点的失败指针走,直到走到一个节点,它的子结点中也有字母为C的节点。然后把当前节点的失败指针指向那个字母也为C的儿子。如果一直走到了root都没找到,那就把失败指针指向root
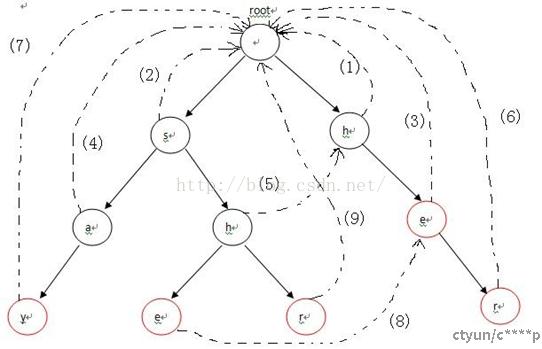
节点处有标记 到达则记录匹配的完整词
Trie 几种实现方法:
Array:内存占用多,只能用于英文等字母表短的
Treemap: O(n*log(t)),t:公共前缀的长度
Hashmap: O(n) Hash计算耗时,且内存仍然可以优化,但灵活性比DAT好很多
DAT:可以看作内存压缩的简单Hash
base[state(s)] + c(字符编码) = state(t)
check[state(t)] = state(s)
核心思想:
base的索引i代表某一个状态state(s)存在这里 使用索引代替状态字符 可以理解为Trie中当前节点的内容
base的值代表当前状态的下一个状态的起始地址 可以理解为Trie中当前节点的地址
加法表示跳转,也可理解为Hash的过程
字符编码不同保证 同一个状态的不同子状态的地址一定不同
流程示例:
开始的时候:base[0] = 0状态0,即空字符串的对应的base[0]值给一个随机值,此处为0.
分析第一个单词(a)从状态为0的空字符串,添加一个a字符,我们来计算单词a的状态:state(a) = base(state(empty)) + code(a)
= base(0) + 1
= 0 + 1
= 1
分析第二个单词(ab)现在已知单词a的状态值为1,将单词ab看作从状态为1的单词a,通过添加一个词b转化而来。state(ab) = base(state(a)) + code(b) = base(1) + 2现在问题是:目前对于状态为1的单词a,它的base(1)的值是空的,还没有赋值。前文所述,base数组里存储的是offset偏移量。这个值是随便给的。我们现在显式给base(1)赋值为0。state(ab) = base(state(a)) + code(b)
= base(1) + 2
= 0 + 2
= 2
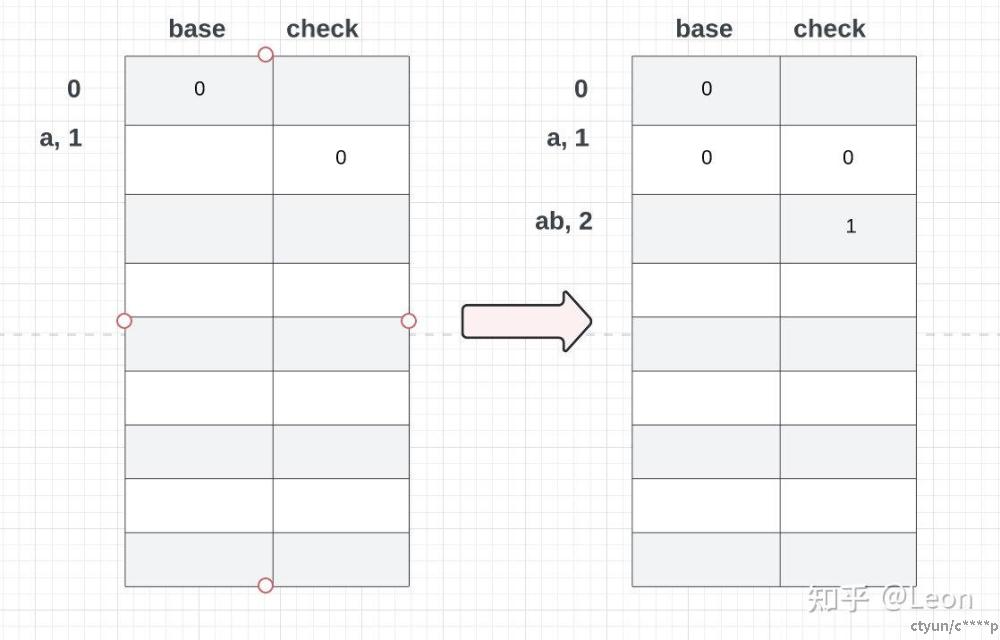
分析第三个单词(bc)
第一字母是b,对应的state(b)通过简单计算(state(b)=base(empty)+code(b)=2)。但是状态2已经被'ab'单词的状态在base[]下标中占用了。
空状态为0的base值,不允许修改了。尽管当初也是随意设定的一个初始值,但后续的a与ab单词的状态都与base(0)值紧密相关。如果修改base(0)的值,那么前面单词a与'ab'计算出的状态值全部需要重新计算。
这个时候,最小的代价是只将单词ab的状态值2进行重新“修正”。怎么计算呢?
之间的ab单词状态是从base(state(a)) + code(b)计算而来。我们当时给state(a)随意设定了一个0值,现在我们重新给一个‘随意’值,比如是6,这个时候state(ab)=base(state(a))+code(b) = 6 + 2 = 8
state(ab) = base(state(a)) + code(b)
= base(1) + 2
= 6 + 2
= 8
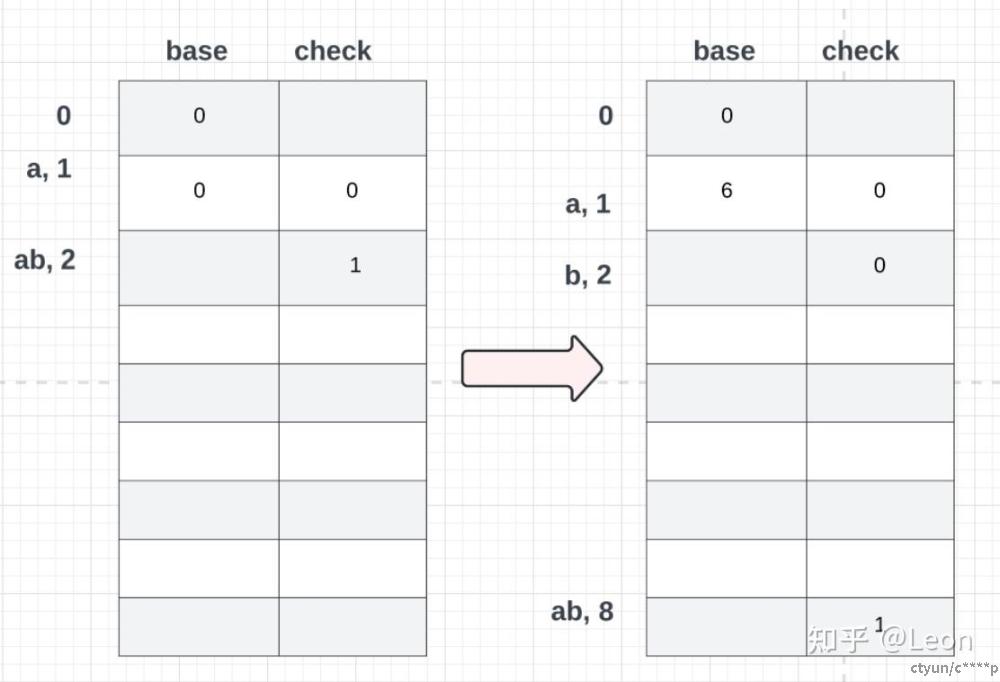
继续添加bc,给状态为2的单词b,‘随意’给定一个base(2)值(此处设置为1)。state(bc) = base(state(b)) + code(c)
= base(2) + 3
= 1 + 3
= 4
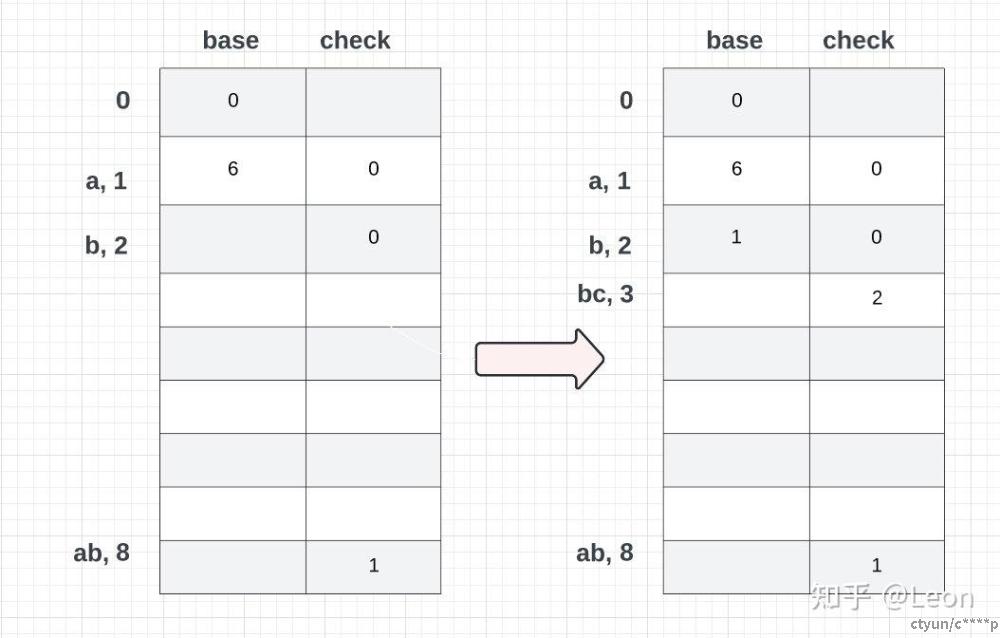
分析第四个单词(bcc)现在已知单词bc的状态值为3,将单词bcc看作从状态为3的单词bc,通过添加一个词c转化而来。state(bcc) = base(state(bc)) + code(c) = base(3) + 3现在问题是:目前对于状态为3的单词bc,它的base(3)的值是空的,还没有赋值。前文所述,base数组里存储的是offset偏移量。这个值是随便给的。我们现在显式给base(1)赋值为2。state(bcc) = base(state(bc)) + code(c)
= base(3) + 3
= 2 + 3
= 5
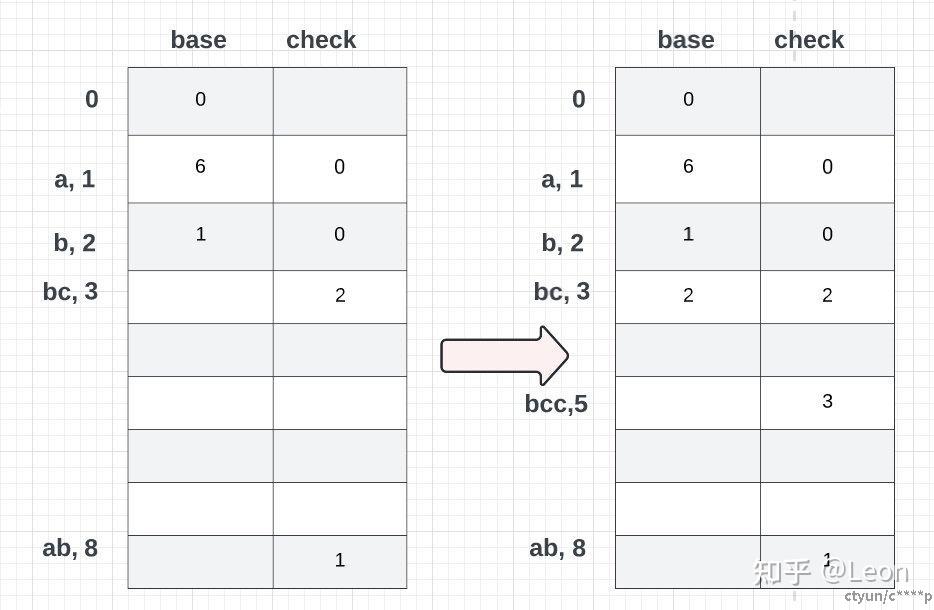
冲突解决方法(base值分配,上述流程中为随机和手动):
线性探查
路径压缩:单个儿子节点压缩成字符串(Patricia Trie)
辅助算法:SAIS(sparse array and induced-sort)
总结:
理论查询速度上限比哈希高,空间占用极小,但状态之间互相依赖,灵活性极差,删除操作极为复杂
适用于一次性构建 对查询性能和内存要求高的场景
ACDAT:
用DAT实现的AC
为一颗双数组Trie树的每个状态(体现为下标)附上额外的信息
为每个状态(base[i]和check[i])构建output[i][]和fail[i]
**原生acdat不支持删除操作 大量删除需要重建**
少量改动时可以标记为已删除 不改动数据 仅从逻辑上删除
性能:
1、利用内存的局部性原理 提高状态转换时的内存命中率从而提高速度:
由于hanlp和goodtool都使用线性探查法解决冲突 在构建的时候 输入挨得近的模式会在内存中离得更近
简单:
构建时按照出现频率对模式排序
复杂·:
三种状态转移对应三个策略:
词内部success的转移:在词中出现频率高的字符编码值小一点 父子状态在内存中离得近一些
有包含关系的词间转移:有包含关系的词放在一起输入
无包含关系的词间转移:常常成对出现的词放在一起输入
编码策略:
综合考虑字符出现在词中/词头的频率 总频率 计算得分根据分值进行排序后按序编码
构建策略:
高频和相邻词放一起输入
2、后缀压缩 无分支的尾缀可以以字符串的形式存储 加速长字符串或者生僻词的匹配速度 模式串分布的比较稀疏的时候 加速效果可能明显一些
基于AC的其他功能:
1、优先以更长的模式分词:
完全包含关系:
若短词和长词没有共同前缀(AABBB AB):叶节点访问完直接返回root
若短词和长词有共同前缀(AAAABBB AA):不设置为匹配完成的节点
非完全包含关系:
长串在前(AAABBB BBC):叶节点访问完直接返回root
长串在后(AAABBB BBCCCDDDDEEEE): 有待处理
多个串重叠(AAABBB BBCCCD CCDEEEFFFFFFFFFFF FFGGGG): 有待处理
策略:
命中所有模式以后 按词长排序 按序逐个分词
2、拼音
两种实现方式:1、以单词为节点进行转移 2、通过空格实现等效功能
HanLP源码阅读:
类:
AhoCorasickDoubleArrayTrie:
成员:Check base fail output数组
方法: dat的构建,接口等
State:
每个节点为一个实例
成员:状态转移表Map<Character, State> success,fail指针 State failure,对应的模式Set<Integer> emits
方法:下一个状态 设置fail指针等
构建:
DAT的构建是dfs,AC自动机fail指针的构建是bfs。故采用异步构造。
1、 构造HashTree 结构的Trie
2、 把HashTree 结构的Trie转换为DAT结构的Trie
3、构建fail指针

调用顺序:addAllKeyword -> addKeyword -> addState
buildDoubleArrayTrie -> resize(分配内存) fetch(获取初始节点) insert(循环插入)
constructFailureStates -> getTransitions(获取状态转移表) nextState failure
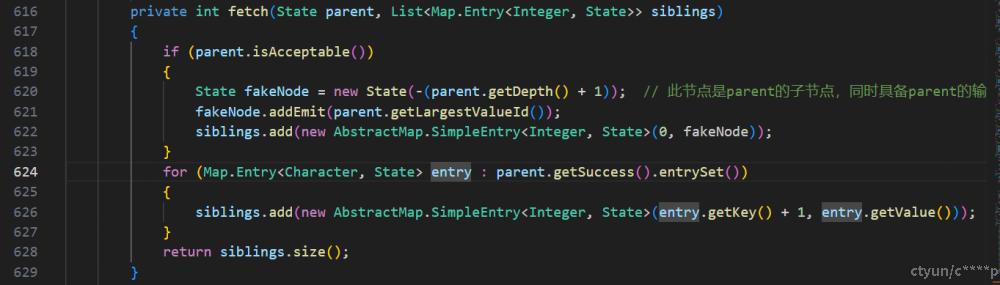
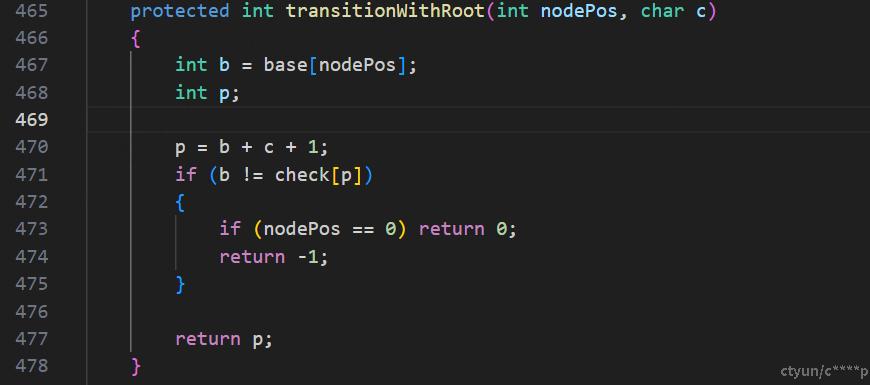
字符编码方式:未实现特殊策略,采用unicode默认编码,在构建DAT获取儿子节点时将character隐式转为整型 第626行 在匹配模式进行转移时将character隐式转为整型第470行
插入方式:
线性探查法
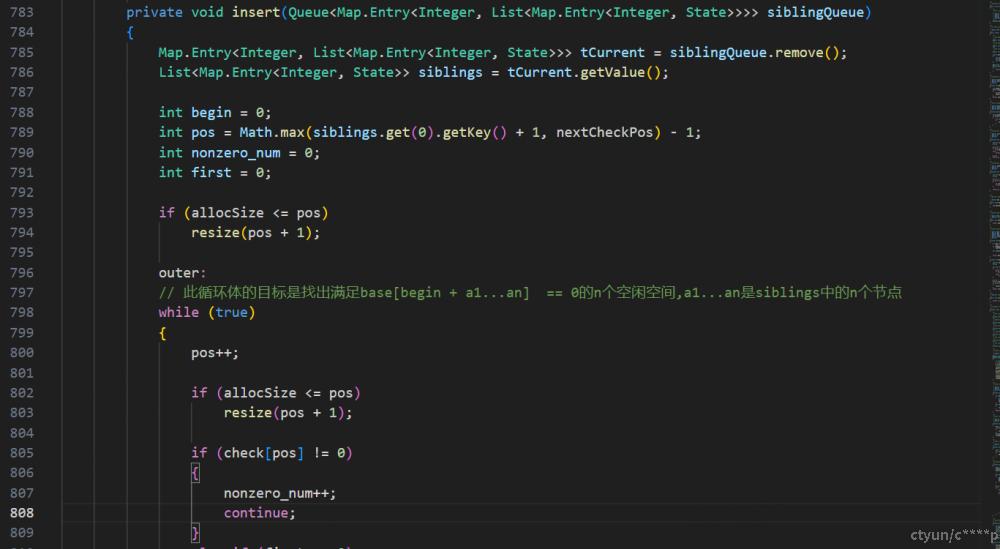
788行和808行 从下标为零开始找空闲的位置
匹配过程:
调用parseText 重写hit
现有ACDAT库:
JAVA:
HanLP
GoodTool
Unicode 编码
线性探查法
使用内存预分配提高分配效率
功能完备 无bug
Python:
Pyahocorasick:
两个问题:
- 一个是关键词匹配不完整,如果目标关键词里面有宝马和马,那么用python的ahocorasick库只会得到宝马,而不会得到马,问题是出在马这个字节是在宝马的链条里面的。
- 另一个是内存泄漏问题
问题在esmre中得到了解决。