背景

自注意力机制需要计算序列中每个元素与其他所有元素的关系，所以它的计算复杂度是O(n^2)，其中n是序列的长度。当序列非常长时，这种​计算复杂度会变得非常高​，导致模型难以处理。

原理

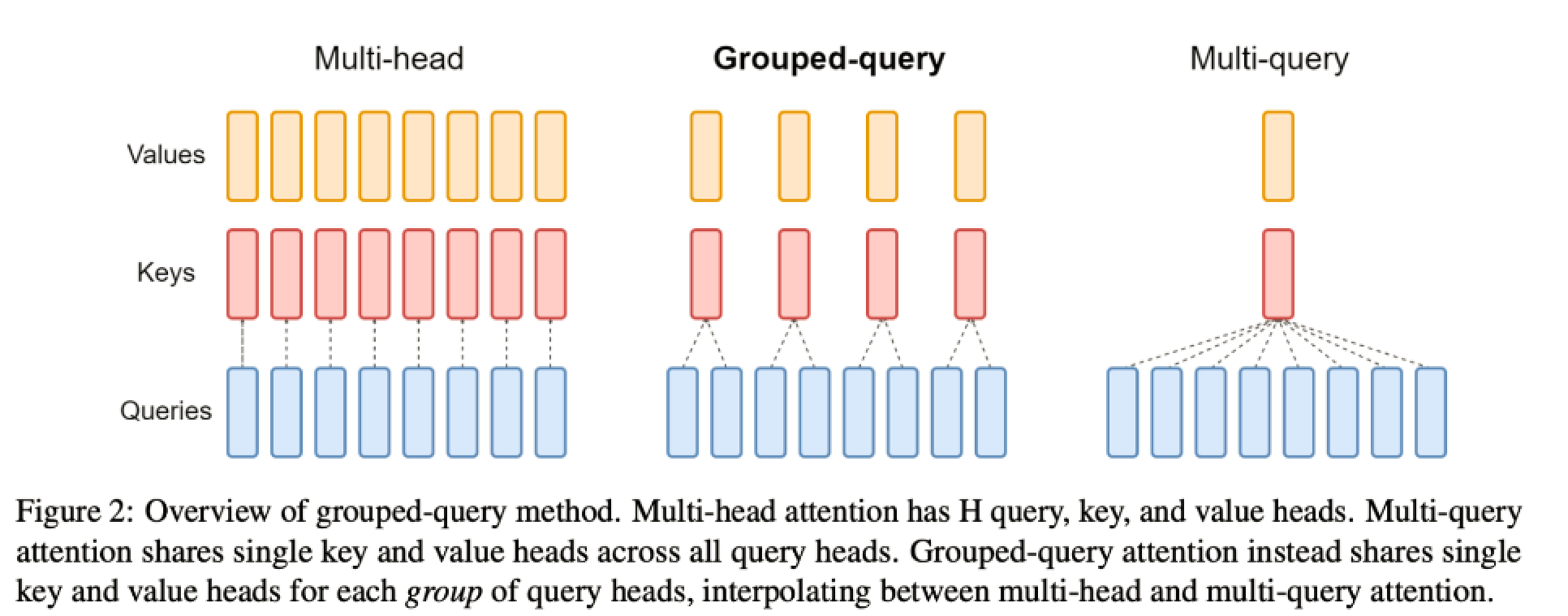
GQA则是为了解决这个问题而提出的。在GQA中，输入序列被分成多个组（Group），每个组内的元素会进行​自注意力计算​，而不同组之间则进行全局注意力计算。这样，每个元素不再需要与所有其他元素进行交互，而只需要与同组的元素和其他组的代表性元素进行交互。这大大降低了计算复杂度，使得模型能够处理更长的序列。

将查询头分成N组，每个组共享一个Key 和 Value 矩阵

具体来说，GQA的计算过程可以分为以下几步：

• 将输入序列分组：输入序列被均匀地​分成多个组​，每个组包含一部分连续的元素。
• 计算组内注意力：每个组内的元素进行自注意力计算，得到组内的上下文表示。
• 计算组间注意力：使用全局注意力机制，计算不同组之间的关系，得到组间的上下文表示。
• 合并组内和组间的上下文表示：将组内和组间的上下文表示​合并​，得到最终的输出序列。
• 通过这种方式，GQA能够有效地处理长序列数据，同时保持了注意力机制的优点，例如能够捕捉序列中的长距离依赖关系。

将MAQ中的key、value的注意力头数设置为一个能够被原本的注意力头数整除的一个数字，也就是group数。

效果

MQA和GQA并​没有减少模型的计算量​，但是模型的==参数量会减少==，优化了显存的换入换出，在解码过程中由于key和value的数量级远远小于query的数量级，所以在自回归解码时可以将已经计算出来的key和value一直高速缓存中，减少数据换入换出的次数，以此来提升速度。

llama2应用

在llama2中有用到GQA, 在推理过程中由于多个query会复用相同的key-value对，所以对于KV-Cache存储会减少对key-value对的存储，减少了 n_heads / n_kv_heads 倍，这里的n_heads是原始Multi-head的头数，n_kv_heads是Grouped-query分组后每组中key-value对的数量。

在实际使用中，会根据从压缩后的key-value对进行还原操作，也就是repeat操作。在llama2中代码如下

def repeat_kv(x: torch.Tensor, n_rep: int) -> torch.Tensor:
    """torch.repeat_interleave(x, dim=2, repeats=n_rep)"""
    bs, slen, n_kv_heads, head_dim = x.shape
    if n_rep == 1:
        return x
    return (
        x[:, :, :, None, :]
        .expand(bs, slen, n_kv_heads, n_rep, head_dim)
        .reshape(bs, slen, n_kv_heads * n_rep, head_dim)
    )