图论是数学中研究图及其性质的一个分支。本文摘要旨在介绍图论的基础知识和主要概念。首先，图是由节点和连接节点的边组成的抽象结构。图可以用来表示各种实际问题，如社交网络、电路和交通网络等。其次，图的基本概念包括顶点、边、路径和环等。顶点是图中的节点，边是连接两个节点的线段，路径是经过一系列节点和边的序列，环是起点和终点相同的路径。进一步，图可以分为有向图和无向图，有向图的边有方向，而无向图的边没有方向。图的表示方法有邻接矩阵和邻接表两种常见的形式。邻接矩阵是一个二维数组，用来表示节点之间的连接关系，邻接表是一个链表或数组的集合，用来表示每个节点的邻居节点。最后，图论有许多重要的应用，如最短路径算法、最小生成树算法和网络流算法等。通过研究图论，人们可以解决各种实际问题，并深入理解图结构的性质和特点。

什么是图

在一个社交网络中，每个帐号和他们之间的关系构成了一张巨大的网络，就像下面这张图：

那么在电脑中，我们要用什么样的数据结构来保存这个网络呢？这个网络需要用一个之前课程里未提到过的数据结构，也就是接下来要讲解的图结构来保存。

到底什么是图？图是由一系列顶点和若干连结顶点集合内两个顶点的边组成的数据结构。数学意义上的图，指的是由一系列点与边构成的集合，这里我们只考虑有限集。通常我们用 G=(V,E) 表示一个图结构，其中V表示点集，E表示边集。

在顶点集合所包含的若干个顶点之间，可能存在着某种两两关系——如果某两个点之间的确存在这样的关系的话，我们就在这两个点之间连边，这样就得到了边集的一个成员，也就是一条边。对应到社交网络中，顶点就是网络中的用户，边就是用户之间的好友关系。

如果用边来表示好友关系的话，对于微信这种双向关注的社交网络没有问题，但是对于微博这种单向关注的要如何表示呢？

于是引出了两个新的概念：有向边和无向边。

简而言之，一条有向边必然是从一个点指向另一个点，而相反方向的边在有向图中则不一定存在；而有的时候我们并不在意构成一条边的两个顶点具体谁先谁后，这样得到的一条边就是无向边。就像在微信中，A是B的好友，那B也一定是A的好友，而在微博中，A关注B并不意味着B也一定关注A。

对于图而言，如果图中所有边都是无向边，则称为无向图，反之称为有向图。

简而言之，无向图中的边是“好友”，而有向图中的边是“关注”。一般而言，我们在数据结构中所讨论的图都是有向图，因为有向图相比无向图更具有代表性。

实际上，无向图可以由有向图来表示。如果AB两个点之间存在无向边的话，那用有向图也可以表示为AB两点之间同时存在A到B与B到A两条有向边。

仍然以社交网络举例：虽然微博中并不存在明确定义的好友关系，但是一般情况下，如果你和另一个 ID 互相关注的话，那么我们也可以近似认为，你和 TA 是好友。

我们来形式化地定义一下图：图是由顶点集合（简称点集）和顶点间的边（简称边集）组成的数据结构，通常用G(V,E)来表示。其中点集用V(G) 来表示，边集用 E(G) 来表示。在无向图中，边连接的两个顶点是无序的，这些边被称为无向边。例如下面这个无向图G，其点集V(G)={1,2,3,5,6}，边集为E(G)={(1,2),(2,3),(1,5),(2,6),(5,6)}。

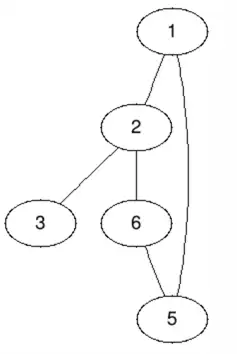
而在有向图中，边连接的两个顶点之间是有序的。箭头的方向就表示有向边的方向。

例如下面这张有向图G'：

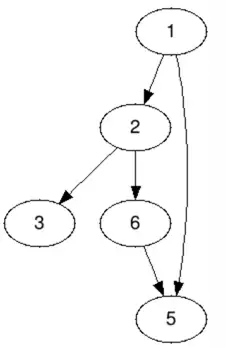
其点集V(G′)={1,2,3,5,6}，边集为E(G′)={(1,2),(2,3),(2,6),(6,5),(1,5)}。对于每条边 (u,v) ，我们称其为从u到v的一条有向边，u是这条有向边的起点，v 是这条有向边的终点。注意在有向图中，(u,v) 和 (v,u) 是不同的两条有向边。

图的分类

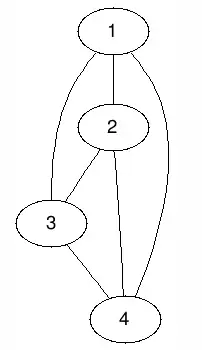
对于一个图，如果以任意一个点为起点，在图上沿着边走都可以到达其他所有点（有向图必须沿有向边的方向），那么这个图就是连通图。显然完全图一定是连通图。

度

定义

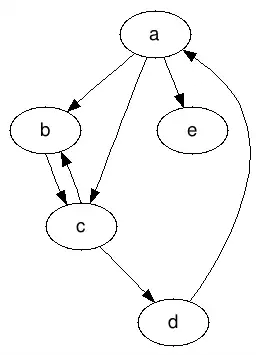
在无向图中，顶点的度是指某个顶点连出的边数。例如在下图中，顶点 b 的度数为3，顶点 a 的度数为4。

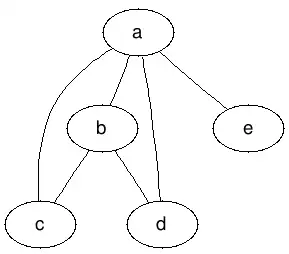
在有向图中，和度对应的是入度和出度这两个概念。顶点的入度是指以该顶点为终点的有向边数量；顶点的出度是指以顶点为起点的有向边数量。需要注意的是，在有向图里，顶点是没有度的概念的。例如在下图中，顶点 a 的入度为1，出度为3；顶点 c 的入度为2，出度为2。

度的性质

在无向图或有向图中，顶点的度数总和为边数的两倍，即：

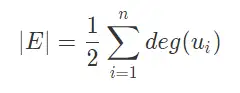
而在有向图中，有一个很明显的性质就是，入度等于出度。
|
|
|
|
|
无向图度数统计

#include <iostream>
using namespace std;
int deg[105];
int main() {
    int n, m;
    cin >> n >> m;
    for (int i = 0; i < m; i++) {
        int u, v;
        cin >> u >> v;
        deg[u]++;
		deg[v]++;
    }
    for (int i = 1; i <= n; i++) {
        cout << deg[i] << " ";
    }
    return 0;
}

有向图度数统计

#include <iostream>
using namespace std;
int outdeg[105], indeg[105];
int main() {
    int n, m;
    cin >> n >> m;
    for (int i = 0; i < m; i++) {
        int u, v;
        cin >> u >> v;
        outdeg[u]++;
        indeg[v]++;
    }
    for (int i = 1; i <= n; i++) {
        cout << outdeg[i] << " " << indeg[i] << endl;
    }
    return 0;
}

图的存储（无权值）

图该怎么存呢？

邻接矩阵

基础知识

什么是邻接矩阵呢？所谓邻接矩阵存储结构就每个顶点用一个一维数组存储边的信息，这样所有点合起来就是用矩阵表示图中各顶点之间的邻接关系。所谓矩阵其实就是二维数组。
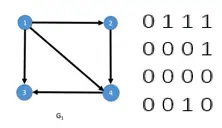
对于有n个顶点的图 G=(V,E) 来说，我们可以用一个 n×n 的矩阵 A 来表示 G 中各顶点的相邻关系，如果 vi 和 vj之间存在边（或弧），则 A[i][j]=1 ，否则 A[i][j]=0 。下图为有向图 G1 和无向图 G2 对应的邻接矩阵：

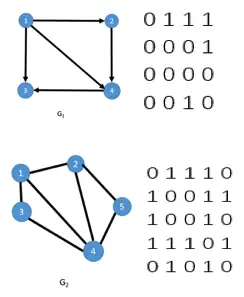
一个图的邻接矩阵是唯一的，矩阵的大小只与顶点个数N有关，是一个 N×N 的矩阵。前面我们已经介绍过，在无向图里，如果顶点 vi 和 vj 之间有边，则可认为顶点 vi 到 vj 有边，顶点 vj 到 vi 也有边。对应到邻接矩阵里，则有 A[i][j]=A[j][i]=1　。因此我们可以发现，无向图的邻接矩阵是一个对称矩阵。

在邻接矩阵上，我们可以直观地看出两个顶点之间是否有边（或弧），并且很容易求出每个顶点的度，入度和出度。

这里我们以 G1 为例，演示下如何利用邻接矩阵计算顶点的入度和出度。顶点的出度，即为邻接矩阵上点对应行上所有值的总和，比如顶点1出度即为0+1+1+1=3；而每个点的入度即为点对应列上所有值的总和，比如顶点3对应的入度即为1+0+0+1=2。

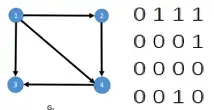
接下来我们就先一起学习构造和使用邻接矩阵的方法。邻接矩阵是一个由1和0构成的矩阵。处于第 i 行、第 j 列上的元素1和0分别代表顶点i到j之间存在或不存在一条又向边。

显然在构造邻接矩阵的时候，我们需要实现一个整型的二维数组。由于当前的图还是空的，因此我们还要把这个二维数组中的每个元素都初始化为0。

在构造好了一个图的结构后，我们需要把图中各边的情况对应在邻接矩阵上。实际上，这一步的实现非常简单，当从顶点x到y存在边时，我们只要把二维数组对应的位置置为1就好了。

用邻接矩阵来构建图需要如下几步，我们可以用二维数组G来表示一个图。

初始化

初始化的过程很简单，只需要把数组初始化为0即可。可以借助memset来快速地将一个数组中的所有元素都初始化为0。（其实定义成全局变量就行了……）

memset(G, 0, sizeof(G));

注意，memset只能用来初始化0和 -1，并且需要加上头文件cstring。

上面的代码等价于：

for (int i = 0; i < N1; i++) { // N1 为数组第一维大小
    for (int j = 0; j < N2; j++) { // N2 为数组第二维大小
        G[i][j] = 0;
    }
}

当然我们平常使用邻接矩阵的时候下标只用 1 到 n 或者 0 到n−1 （这个看题目中点的编号）。

插入边

如果插入一条无向边 (u,v) ，只需要

G[u][v] = 1;
G[v][u] = 1;

也可以写成G[u][v] = G[v][u] = 1;。
如果插入一条有向边 (u,v) ，只需要G[u][v] = 1;。

访问边

如果G[u][v] = 1，说明有一条从 u 到 v 的边，否则没有从 u 到 v 的边。

邻接矩阵的使用

#include <iostream>
using namespace std;
const int maxn = 105;
int G[maxn][maxn];
int main() {
    int n, m;
    cin >> n >> m;
    for (int i = 0; i < m; i++) {
        int u, v;
        cin >> u >> v;
		G[u][v] = G[v][u] = 1;
    }
    for (int i = 1; i <= n; i++) {
        for (int j = 1; j <= n; j++) {
            cout << G[i][j] << " ";
        }
        cout << endl;
    }
    return 0;
}

邻接表

邻接表的思想是，对于图中的每一个顶点，用一个数组来记录这个点和哪些点相连。由于相邻的点会动态的添加，所以对于每个点，我们需要用vector来记录。

也就是对于每个点，我们都用一个vector来记录这个点和哪些点相连。比如对于一张有 10 个点的图，vector<int> G[11]就可以用来记录这张图了。对于一条从 a 到 b 的有向边，我们通过G[a].push_back(b)就可以把这条边添加进去；如果是无向边，则需要在G[a].push_back(b)的同时G[b].push_back(a)。

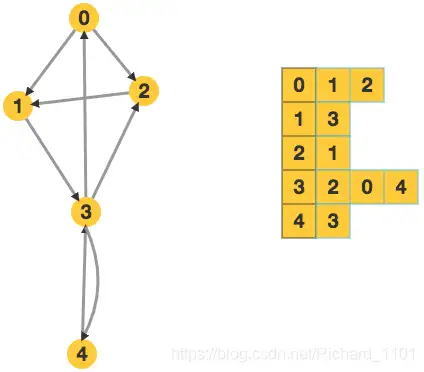
上图演示了一个图对应的邻接表。每一行的第一列表示的是最外层vector数组的下标。

邻接表的优缺点

优点

1. 节省空间：当图的顶点数很多、但是边的数量很少时，如果用邻接矩阵，我们就需要开一个很大的二维数组，最后我们需要存储 n*n 个数。但是用邻接表，最后我们存储的数据量只是边数的两倍。
2. 可以记录重复边：如果两个点之间有多条边，用邻接矩阵只能记录一条，但是用邻接表就能记录多条。虽然重复的边看起来是多余的，但在很多时候对解题来说是必要的。

缺点

当然，有优点就有缺点，用邻接表存图的最大缺点就是随机访问效率低。比如，我们需要询问点 a 是否和点 b 连，我们就要遍历G[a]，检查这个vector里是否有 b 。而在邻接矩阵中，只需要根据G[a][b]就能判断。

因此，我们需要对不同的应用情景选择不同的存图方法。如果是稀疏图（顶点很多、边很少），一般用邻接表；如果是稠密图（顶点很少、边很多），一般用邻接矩阵。

当点数较多（多于 5000）时，使用邻接矩阵会超出空间限制，需要使用邻接表。

邻接表的实现

#include <iostream>
#include <vector>
using namespace std;
const int maxn = 105;
vector<int> G[maxn];
int main() {
    int n, m;
    cin >> n >> m;
    for (int i = 0; i < m; i++) {
        int u, v;
        cin >> u >> v;
        G[u].push_back(v);
        G[v].push_back(u);
    }
    for (int i = 1; i <= n; i++) {
        cout << i << " : ";
        for (int j = 0; j < G[i].size(); j++) {
            cout << G[i][j] << " ";
        }
        cout << endl;
    }
    return 0;
}

图的存储（带权值）

邻接矩阵

在前面，图中的边都只是用来表示两个点之间是否存在关系，而没有体现出两个点之间关系的强弱。比如在社交网络中，不能单纯地用0、1来表示两个人否为朋友。当两个人是朋友时，有可能是很好的朋友，也有可能是一般的朋友，还有可能是不熟悉的朋友。

我们用一个数值来表示两个人之间的朋友关系强弱，两个人的朋友关系越强，对应的值就越大。而这个值就是两个人在图中对应的边的权值，简称边权。对应的图我们称之为带权图。

如下就是一个带权图，我们把每条边对应的边权标记在边上：

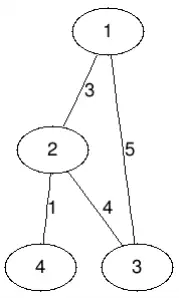
带权图也分成带权有向图和带权无向图。前面学到的关于图的性质在带权图上同样成立。实际上，我们前面学习的图是一种特殊带权图，只不过图中所有边的权值只有1一种；而在带权图中，边的权值可以是任意的。

用邻接矩阵存储带权图和之前的方法一样，用G[a][b]来表示 a 和 b 之间的边权（我们需要用一个数值来表示边不存在，如0）。同样，对于无向图，这个矩阵依然是对称的。

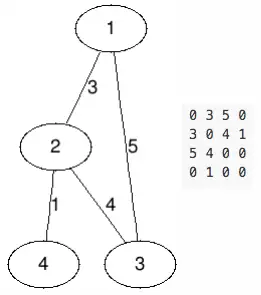
如上所示，左边的图对应的右边的邻接矩阵

带权图的邻接矩阵

#include <iostream>
#include <cstring>
using namespace std;
const int maxn = 105;
int G[maxn][maxn];
int sum[maxn];
int main() {
    int n, m;
    cin >> n >> m;
    for (int i = 0; i < m; i++) {
        int u, v, w;
        cin >> u >> v >> w;
		G[u][v] = w;
    }
    for (int i = 1; i <= n; i++) {
        for (int j = 1; j <= n; j++) {
            cout << G[i][j] << " ";
        }
        cout << endl;
    }
    for (int i = 1; i <= n; i++) {
        for (int j = 1; j <= n; j++) {
            sum[i] += G[i][j];
        }
    }
    for (int i = 1; i <= n; i++) {
        cout << sum[i] << " ";
    }
    return 0;
}

邻接表

用邻接表存储带权图和之前的实现方式略有区别，我们需要用一个结构体来记录一条边连接的点和这条边的边权，然后用一个vector来存储若干个结构体，实际上就是把一个点所连接的点以及这条边的边权"打包"起来放到邻接表中。

结构体的定义举例如下：

struct node {
    int v;  // 用来记录连接的点
    int w;  // 用来记录这条边的边权
};

我们通常把有向图中加入一条边写成一个函数，例如加入一条有向边 (u,v) 、边权为 w ，就可以用如下的函数来实现（我们需要把图定义成全局变量）。

vector<node> G[105];
// 插入有向边
void insert(int u, int v, int w) {
    node temp;
    temp.v = v;
    temp.w = w;
    G[u].push_back(temp);
}

而插入一条无向边，实际上相当于插入两条方向相反的有向边：

// 插入无向边
void insert2(int u, int v, int w) {
    insert(u, v, w);
    insert(v, u, w);
}

带权图邻接表的实现

#include <iostream>
#include <vector>
using namespace std;
const int maxn = 105;
struct node {
    int v;
    int w;
};
vector<node> G[maxn];
void insert(int u, int v, int w) {
    node temp;
    temp.v = v;
    temp.w = w;
    G[u].push_back(temp);
}
int main() {
    int n, m;
    cin >> n >> m;
    for (int i = 0; i < m; i++) {
        int u, v, w;
        cin >> u >> v >> w;
        insert(u, v, w);
    }
    for (int i = 1; i <= n; i++) {
        for (int j = 0; j < G[i].size(); j++) {
			cout << i << " " << G[i][j].v << " " << G[i][j].w << endl;
        }
    }
    return 0;
}

欢迎大家指出错误或给出建议