1. 概述
Apache Spark有一个经典的示例Spark Pi,该示例使用 Apache Spark 计算圆周率(π)的示例程序。 在基本原理上,该应用程序基于蒙特卡洛方法,这是一种随机抽样技术,用于估计难以直接计算的问题的答案。
2. 蒙特卡洛方法原理简介
蒙特卡洛方法(Monte Carlo method)是一种基于概率论和统计的数值计算方法。这种方法使用随机抽样来解决各类问题,特别是那些难以通过传统分析方法处理的问题。它的核心思想是利用大量随机样本对复杂系统进行大量模拟,从而获得精确或近似的解决方法。
蒙特卡洛方法的基本步骤通常包括:
-
定义模型:首先,需要将问题转化为一个可以被模拟的概率模型。这可能涉及到确定变量、参数以及它们之间的关系。
-
生成随机数:根据模型中各个变量的概率分布,生成大量的随机数。这些随机数代表了问题中的不确定性或随机性。
-
执行模拟:使用这些随机数作为输入,运行模拟以产生输出结果。模拟过程可能会涉及多次迭代或实验。
-
收集结果:从每次模拟运行中收集数据,然后汇总所有结果。
-
分析结果:通过对模拟结果的分析,提取出所需的统计信息,如平均值、方差等,并据此推断关于原问题的结论。
蒙特卡洛方法在许多领域都有应用,例如金融风险管理、物理学、工程学、计算机科学、生物学、化学、气候学等等。它的一个显著优点是可以处理多维问题,并且不需要复杂的数学分析。然而,其缺点是计算量大,尤其是在需要高精度的情况下。
3. Spark Pi如何通过蒙特卡洛原理来计算π
通过阅读Spark Pi的源码,我们可以得到以下步骤;
首先,Spark会生成随机点,在 2D 平面上随机选择 n 个点,这些点通常由其 x 和 y 坐标表示,范围从 -1 到 1,而点的位置是均匀分布的,也就是说,任何特定区域被选中的概率与其面积成正比;
接着会检查检查点是否在单位圆内,对于每个生成的点,通过检查该点与原点的距离是否小于或等于 1 来确定该点是否位于半径为 1 的单位圆内,如果点到原点的距离小于或等于 1,则认为该点在圆内;
然后统计落在圆内的点数,也就是计算所有随机点中落在圆内的点的数量,并记为 count;
最后是估算 π,根据蒙特卡洛原理,我们知道:如果将一个边长为 2 的正方形和一个半径为 1 的圆放在同一个坐标系中,那么圆的面积占正方形面积的比例应该接近于 π/4,因此,我们可以通过以下公式来估算 π:pi_estimate = 4 * (count / n)
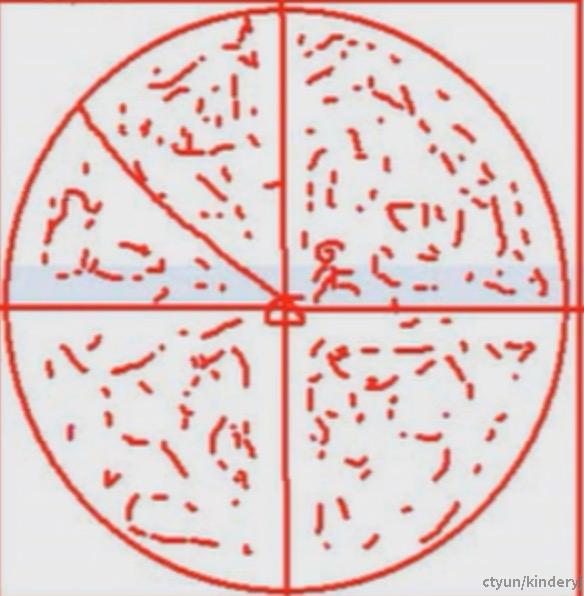
Spark是一个分布式计算框架,因此Spark也是基于分布式的方式对π 进行批量的计算和执行,具体来说,Spark 将数据集分割成多个部分(称为分区),并将这些分区分发给集群中的不同工作节点进行处理,每个工作节点都会独立地生成随机点、检查它们是否在圆内,并累加本地计数器,最后,Spark 会汇总各个工作节点的结果,以得到最终的 π 估计值。