率失真定理
率失真定理(Rate-Distortion Theory)是信息论中的一个重要理论,用于描述在特定码率下,信源信号的最小期望失真。它是信息论的主要分支之一,也是进行数据压缩和信源编码的理论基础之一。
率失真定理可以被描述为:对于一个给定的信源分布和失真度量,在特定的码率下,能够达到的最小期望失真是多少,或者为了满足一定的失真限制,最小的描述码率是多少。换句话说,率失真定理研究的是在码率和失真之间的权衡关系。如下图示意:
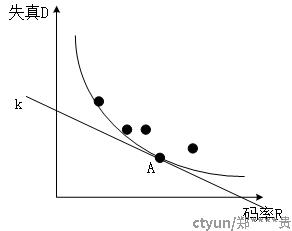
率失真定理的应用非常广泛,包括量化、数模转换、数据压缩等领域。它在数据传输和存储中起着重要的作用,可以帮助我们在不同的码率和失真要求下,选择合适的压缩算法和编码方案。
RDT的应用
在视频编码中,我们通常关心两个主要的问题:视频质量(如清晰度和颜色准确性)和文件大小。通过使用RDT,我们可以找到一个平衡点,使得这两个因素都能得到满足。例如,如果我们想要提高视频质量,我们可以使用一个更好的编码算法,但这可能会导致文件大小增加。反之,如果我们想要减小文件大小,我们可能需要接受一些视频质量的牺牲。通过应用RDT,我们可以找到最佳的编码策略,以达到最佳的质量和文件大小比例。具体而言,RDT的应用可以大致体现在码率控制、编码方案选择两大方面。
码率控制
RDT可以用于视频编码中的码率控制算法。码率控制是视频编码中的一个重要技术模块,通过调整视频的码率来控制视频的质量和压缩效率。RDT可以帮助确定在特定的码率下,达到的最小期望失真是多少,从而在编码过程中进行合理的码率控制。如下图示意:
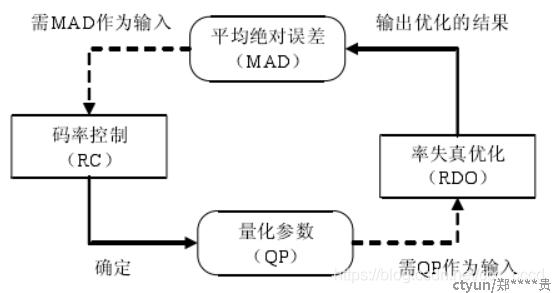
具体来说,RDT在视频编码码率控制上的应用包括以下几个方面:
-
码率控制算法设计:RDT可以用于设计视频编码中的码率控制算法。通过分析信源信号的特性和失真度量,结合RDT的理论基础,可以设计出适应不同码率和失真要求的码率控制算法。这些算法可以根据RDT的结果,动态地调整视频的码率,以达到预期的失真水平。
-
码率调整:RDT可以帮助视频编码器根据当前的码率和失真要求,动态地调整视频的码率。通过实时监测视频的失真情况,结合RDT的理论模型,可以根据当前的码率和失真水平,自适应地调整视频的码率,以保证视频的质量和压缩效率。
-
码率预测:RDT可以用于预测视频在不同码率下的失真水平。通过建立码率和失真之间的模型,可以根据给定的码率,预测视频的失真程度。这样可以在编码过程中,根据预测的失真水平,进行合理的码率控制,以达到预期的失真要求。
RDT在视频编码中的码率控制应用非常广泛。它可以帮助设计码率控制算法,动态调整视频的码率,预测视频在不同码率下的失真水平,以实现高质量的视频编码和传输。
编码方案选择
RDT可以用于视频压缩算法的设计和优化。视频压缩是视频编码的核心任务之一,通过减少视频数据的冗余性和不必要的信息,来实现对视频数据的压缩。RDT可以帮助我们在不同的码率和失真要求下,选择合适的压缩算法和编码方案,以达到最佳的压缩效果。如下图示意:
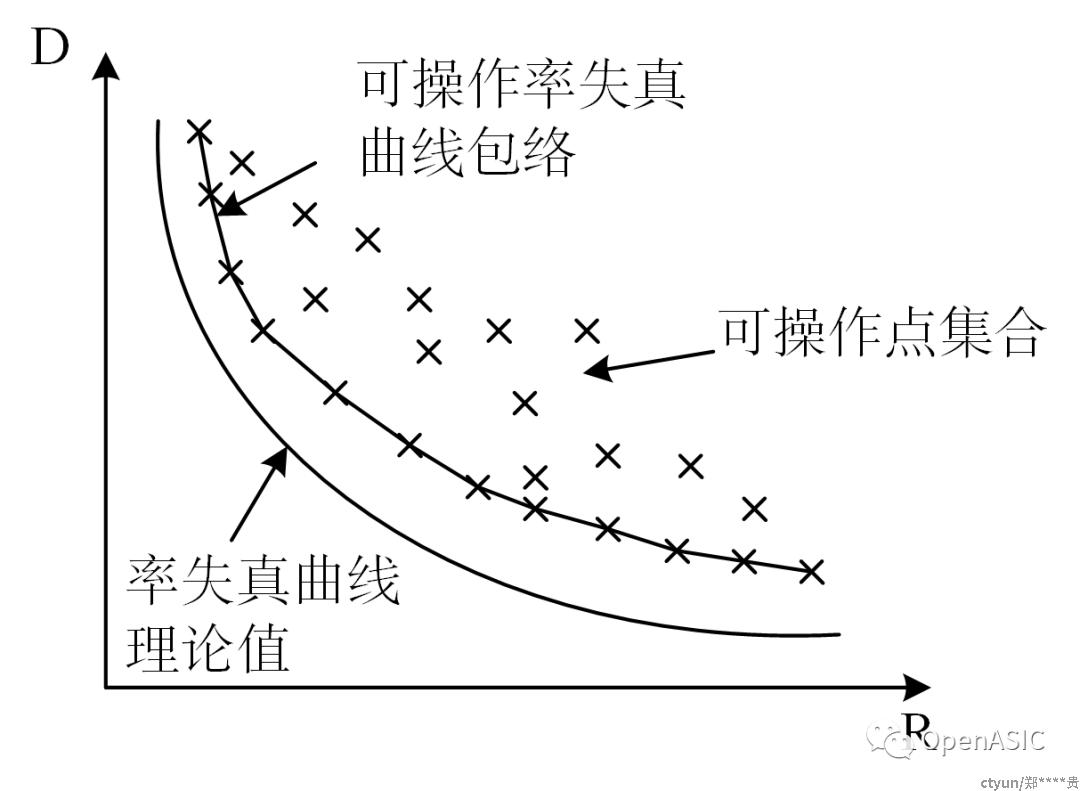
具体来说,RDT在视频编码中的方案选择应用包括以下几个方面:
-
码率和失真之间的权衡:RDT可以帮助我们理解码率和失真之间的权衡关系。通过分析不同码率下的失真水平,我们可以选择合适的码率来控制视频的质量和压缩效率。RDT可以提供理论基础和指导,帮助我们在方案选择中做出权衡决策。
-
编码参数优化:RDT可以用于优化编码参数的选择。通过建立码率和失真之间的模型,我们可以根据预期的失真要求,选择合适的编码参数,如量化参数、帧率等。RDT可以帮助我们在方案选择中找到最佳的编码参数组合,以达到预期的压缩效率和视频质量。
-
算法选择:RDT可以用于选择合适的编码算法。不同的编码算法在压缩效率和视频质量方面可能存在差异。通过分析不同算法在不同码率下的失真水平,结合RDT的理论基础,我们可以选择适合特定应用场景的编码算法,以达到最佳的方案选择。
RDT在视频编码中的方案选择应用非常重要。它可以帮助我们理解码率和失真之间的权衡关系,优化编码参数的选择,以及选择合适的编码算法。通过合理应用RDT,我们可以实现高效的视频编码和传输。
RDT在H.264中的应用
H.264编码中的率失真优化是通过使用基于Lagrangian优化算法的率失真优化模型来实现的。具体步骤包括确定目标函数、确定约束条件、计算拉格朗日乘子、优化过程和结果评估。这些步骤通过调整码率和失真之间的权衡关系,以达到在给定码率下最小化失真的目标。
-
确定目标函数:首先,需要定义一个目标函数,该函数将码率和失真进行权衡。通常,目标函数由码率和失真的加权和构成,其中拉格朗日乘子用于平衡两者之间的关系。
-
确定约束条件:在进行优化之前,需要确定一些约束条件,例如最大码率或最小失真等。这些约束条件将在优化过程中起到限制作用。
-
计算拉格朗日乘子:通过引入拉格朗日乘子,将约束条件融入到目标函数中。拉格朗日乘子是一个权重系数,用于平衡码率和失真之间的关系。通过调整拉格朗日乘子的值,可以实现在给定码率下最小化失真的目标。
-
优化过程:基于Lagrangian优化算法,通过迭代的方式逐步优化目标函数。在每一次迭代中,根据当前的拉格朗日乘子的值,计算目标函数的梯度,并更新码率和失真的值。通过不断迭代,逐步接近最优解。
-
结果评估:在优化过程结束后,需要对优化结果进行评估。可以通过计算实际码率和失真的值,以及与预期目标的差距来评估优化效果。
结论
总的来说,率失真定理在视频编码中发挥着重要的作用。它为我们提供了一个理论框架,可以帮助我们理解和优化视频编码过程,以达到最佳的视频质量和文件大小。随着视频编码技术的不断发展,我们期待看到更多利用RDT的理论和实践的应用。