ceph可靠性
ceph通过CRUSH算法和Monitor集群的方法,在架构上保证了去中心化并消除了单点故障,除此之外Ceph还要保证集群中存储数据的高可靠性。
保证数据的高可靠性主要有两种方式:
数据冗余备份
纠删码机制
磁盘的年损坏率大约是7%,工业可接受的可靠性大约是11个9以上(99.999999999%)
多副本
Ceph在后台自动存储数据的多个副本,从而保证在硬盘损坏、服务器故障、机柜停电等情况下,数据不会丢失,甚至数据仍能保持在线。
Ceph需要及时进行故障恢复,将丢失的数据副本补全,以维持数据的高可靠性。
用户可以配置每个存储池的多副本策略,即每个存储池可以有各自的副本数量。
|
策略 |
冗余度 |
可靠性 |
|
2副本 |
200% |
99.999999% |
|
3副本 |
300% |
99.9999999999% |
纠删码
纠删码是一种编码技术,用1.5副本的空间就可以实现丢失任意两块数据都可以恢复出原始数据的效果,但纠删码的缺点是编码和恢复的代价大。
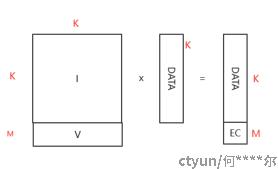
Ceph对k个同样大小的数据块, 额外增加m个校验块, 以使得这k+m块数据中任意丢失m块时都能把丢失的数据找回。
|
策略 |
冗余度 |
可靠性 |
|
4+2 |
150% |
99.999999999% |
|
8+3 |
137.5% |
99.999999999997% |
|
8+2 |
125% |
99.99999999% |
多副本和纠删码
|
比较项 |
多副本(N) |
纠删码(K+M) |
|
可用容量 |
1/N |
K/K+M |
|
容忍节点故障数量 |
N-1 |
M |
|
读写性能 |
较高 |
较低 |
|
重构性能 |
较快 |
较慢 |
|
使用场景 |
小文件场景 热数据 |
大文件场景 冷数据 |
EC原理
k+1
冗余求和 y1 = d1+d2+d3
k+2
方程组 {y1 = d1+d2+d3 y2 = d1+2d2+4d3}
k+m
方程组 {y1 = d1+d2+d3 y2 = d1+2d2+4d3 y3 = d1+3d2+9d3}
两点确定一条直线
包含未知数d1,d2的直线:y = d1+d2 x
已知直线上两点:x1=1,y1=11;x2=2,y2=17
校验块和数据块的关系: {y1 = d1+d2 y2 = d1+2d2 }
高次曲线
如果有k个未知数据块, 把k个数据作为系数, 定义1条关于x的高次曲线:
y=d1+d2x+d3x2+...+dkx(k−1)
取m个不同的x的值(1, 2, 3…m), 记录这条曲线上m个不同点的坐标,平面上m个点可以唯一确定1条 m-1 次幂的曲线(或通过m个点跟k-m个已知系数确定一条k-1次幂的曲线).确定了这条关于x的曲线,就找回了它的系数,也就是数据块
EC实现——编码
生成纠删码
y1=d1+1d2+12d3+⋯+1k−1dk
y2=d1+2d2+22d3+⋯+2k−1dk
y3=d1+3d2+32d3+⋯+3k−1dk
⋯
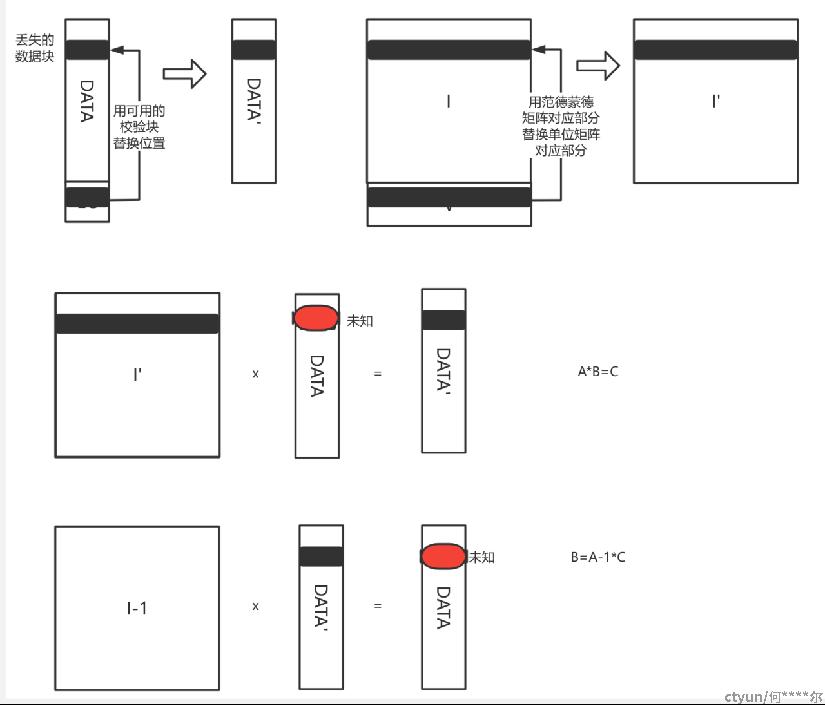
EC实现——解码
求解n元一次方程

只要 xᵢ 都不同, 则 Vandermonde 矩阵的行列式就不为0, 矩阵可逆, 表示方程有唯一解.