前言

本文旨在介绍一种支持并发读写的无锁哈希表结构。其核心思想来源于两篇论文：

1. Michael, M. M. High performance dynamic lock-free hash tables and list-based sets. In Proceedings of the fourteenth annual ACM
   symposium on parallel algorithms and architectures, ACM Press, (2002), 73-82.
2. Ori Shalev and Nir Shavit. Split-ordered lists: Lock-free extensible hash tables. J. ACM 53, 3 (May 2006), 379-405.

其中，第一篇论文重点介绍了无锁单链表的实现原理。有了这篇论文，已经可以实现无锁哈希表了（将冲突链替换为论文中表述的无锁单链表）。第
二篇论文更进一步，提出“分裂排序表”的概念，实现了无锁哈希表的动态扩容。基于第二篇论文的分裂排序表已经在URCU库中实现，参考：https://github.com/urcu/userspace-rcu。

声明：本文仅仅是对上述两篇论文以及URCU库代码进行翻译整理，帮助读者理解无锁哈希表基本原理。论文中介绍的算法，以及URCU库中的代码实现，版权归原作者所有。

哈希表的并发问题

众所周知，哈希表的结构大致如下：

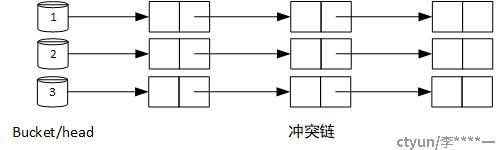
要实现无锁的哈希表（即允许多线程并发地添删改查，却不用加锁），需要解决两个问题：

1. 如何实现冲突链的并发访问
2. 如何保证元素释放时不被其他线程访问

业界的常规实现方式有两种：

1. 变多线程访问为单线程访问
   说白了就是分Core分表，即每个线程独享自己的哈希表。使用特殊设计的哈希算法，让命中这个线程的流量仅仅被哈希到同一个线程上。
   这确实解决了哈希表的并发访问问题，但是却引入了很多限制：一旦流量处理过程中出现NAT或NAPT（地址换换，端口地址转换），则对称哈希算法则会失效。
2. 在桶上加互斥锁或者读写锁。这会严重影响性能。而且写饥饿也不好处理。

 

这里举一个多线程添加元素的例子，说明并发访问场景下，链表是如何被破坏的。这里假定指针的赋值是原子的（实际上不原子，但是可以以原子方式使用，另外乱序执行问题也不在这里讨论）

我们首先看一下，如果不加锁地访问哈希表，会造成什么后果。为了简化描述，我们定义线程A为当前线程，而线程B做为“干扰者”。然后按照主线程A的操作分类描述。我们定义单链表被操作之前的样子如下：

正常场景（单线程）

单线程在单链表中增加一个元素，操作仅需要两步。这里假定我们想在N1和N2之间插入新元素New，其步骤如下：

第一步，申请一个新节点，让其后继指针指向N2。

 

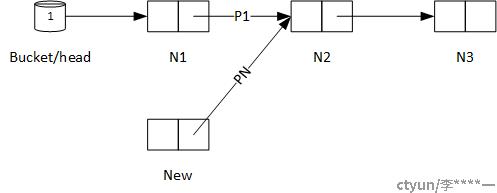
第二步，将N1的后继指针P1指向新加入的元素NEW即可。

 

当然，这是没有其他线程干扰的情况。我们看下其他线程是如何干扰线程A的。

干扰场景（多线程）

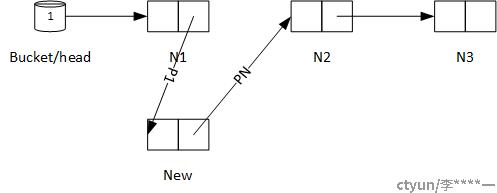
考虑到当线程A执行到第一步和第二步之间的时候，有另外一个线程B也想在同一位置插入节点NEW‘，则会出现以下情况：

1、两个线程同时申请了内存，同时将新节点的后继指针指向N2.

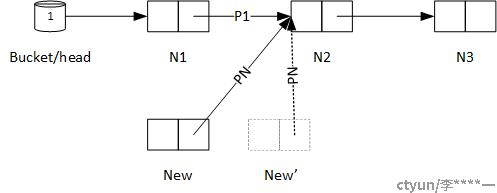
2、然后进程B先修改P1指针，进程A后修改P1指针，则线程B的修改被覆盖，最终的链表将会是下面这个样子：

 

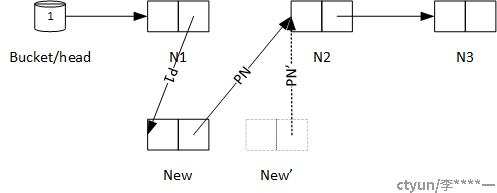
显然，元素New'丢失了。链表同样被破坏的场景，还有在线程A运行时，N1被删除的情况，会酿成更为严重的后果。

无锁链表的实现原理

无锁链表的实现思路，还是CAS操作。 如果某次操作和预期结果不一样，则会放弃当前操作，然后再次尝试。

数据结构

我们先定义一组相关的数据结构：

// types and structures structure NodeType {      /* Node */     Key : KeyType;                        /* typeval */     <Mark,Next,Tag> : <boolean,*NodeType,TagType>;       /* CASMarkNode“”nexttagABA */ } structure MarkPtrType {    /* Markkey */     <Mark,Next,Tag> : <boolean,*NodeType,TagType>;       /* NodeType */ } // T is the hash array // M is the number of hash buckets T[M] : MarkPtrType;    // Initially <0,null,dontcare>     /* M */

还是要说一下<Mark,Next,Tag>的内存分布：所有这三个字段都是放在两个字中的，两个字需要小于等于机器字长，以便于可以一次访问。这是CAS操作必须的。Next指针在主流机器上是按照单字对齐的（而且它的最后一个bit总是0，可以拿出来使用）。而mark正好使用了这个bit。Tag可以单占一个字。所有以上三个元素可以占用两个相邻字。

哈希表操作函数

哈希表的操作函数定义如下：

// Hash function h(key:KeyType):0..M-1 { ... } /* 0 M-1 */         // Hash table operations         HashInsert(key:KeyType):boolean { /* */         // Assuming new node allocations always succeed         nodeAllocateNode(); /* node */         nodeˆ.Keykey; /* keynodekey^.*/         if Insert(&T[h(key)],node) return true; /* T[h(key)]nodetruenodefalse */         FreeNode(node); return false; } HashDelete(key:KeyType):boolean { /* keyT[h(key)]node */         return Delete(&T[h(key)],key); } HashSearch(key:KeyType):boolean { /* keyT[h(key)] */         return Search(&T[h(key)],key); }

可见，哈希表的操作，是严重依赖单链表的操作的。如果链表的操作是无锁的，那么，哈希表的操作也可以是无锁的（除了哈希比表的总台扩缩容，这个后面讨论）。下面介绍链表的操作。

链表操作函数

私有变量定义

先定义一组私有变量。在后续的链表操作中会被用到：

// private variables prev : *MarkPtrType; /* */ <pmark,cur,ptag> : MarkPtrType; /* marktag */ <cmark,next,ctag> : MarkPtrType; /* marktag */

 

在介绍操作函数之前，有必要介绍一下find函数。后面几乎都用到了。而find函数对上述私有变量的赋值，对理解代码至关重要。

find函数返回一个bool变量，指示匹配key的node是否存在。不管那种情况，当它完成时，它都会对prev, <cur,ptag> and <next,ctag> 进行赋值，这相当于对当前Find操作的一段list元素做了个快照。这个快照包含这样一个node和它的前驱指针：这个node的key刚好大于或者等于输入的key。Find操作保证在某一时刻，当*prev（prev指向的内容）处于链表中时，*prev的内容是<0,cur,ptag>。【译者按：这个就是‘当前节’的上一个节点A，0表示A没有被删除，curr意思是A的next指针指向的就是“当前节点”，ptag当然就是A节点的tag。这里“保证”的意思，是若pmark不是0，它会重复再次执行，直到pmark是0位置。“某一时刻”也就是这个意思。】 并且，如果cur不是NULL，在这个时刻，cur指向的成员curˆ.<Mark,Next,Tag>刚好是<0,next,ctag>【译者按：cur指向的当然是当前节点的下一个节点C了。<0,next,ctag>的意思是，C没有被删除，next是C的next指针，ctag就是C的tag。也就是说，当前节点的下一个节点也不能是已经被删除的节点。】并且cur的key刚好大于或者等于输入key。如果cur等于NULL，则代表list中所有节点的key都比输入的key小。

我们再画图说明一下：

 

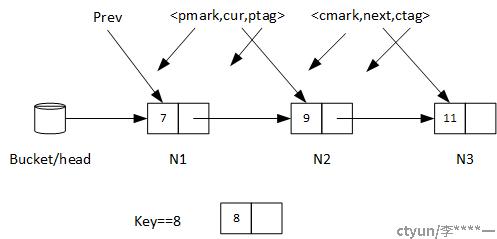
如上图所示。链表中已有元素key分别为7、9、11，待插入节点key为8。则当Find函数返回时，cur应该指向N2，而prev指向N1，next指向N3。并且，pmark只能是0，cmark也只能是0。（不是0就重新执行，直到这两个值是0为止。）

这样，其实是找到了一个“正确的位置”，另外找到了一个“正确的时机”。

插入操作

Insert(head:*MarkPtrType,node:*NodeType):boolean { /* bool */         keynodeˆ.Key; /* nodekeykey */         while true {                 A1: if Find(head,key)                 return false; /* false */                 A2: nodeˆ.<Mark,Next> <0,cur>; /* 0cur nodemarknext */                 A3: if CAS(prev,0,cur,ptag,0,node,ptag+1) /* CASprevcurnodeCASprevnodepmark0ptagwhile true*/                 return true;         } }

画图说明：

我们还是用上面那个图举例。它代表代码运行至A1时的样子。

当代码运行至A2时，这一步实际上是将新增节点的后继指针指向了N2（即cur指向的节点）：

 

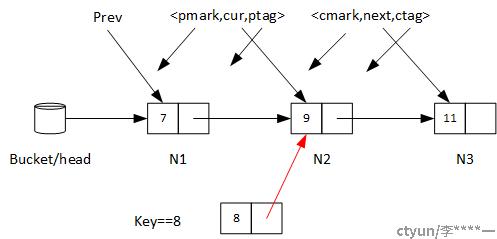
当代码运行至A3时，实际上是将N1的后继指针指向了即将插入的节点。

 

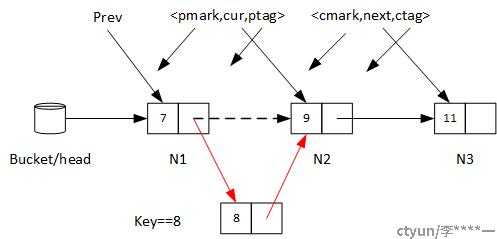
CAS操作CAS(prev,0,cur,ptag,0,node,ptag+1)保证了此时此刻：N1没有被标记为删除，cur指针没有被其他线程修改，而且ptag没有变化（预防ABA问题），这就排除了N1正在被删除、N2正在被删除，或者N2之前正在被插入新元素的情况。所以单链表不会被破坏。

删除操作

Delete(head:*MarkPtrType,key:KeyType):boolean {         while true {                 B1: if !Find(head,key) return false; /* keyfalse */                 B2: if !CAS(&curˆ.<Mark,Next,Tag>, <0,next,ctag>, <1,next,ctag+1>) /* */                         continue;                 B3: if CAS(prev,<0,cur,ptag>,<0,next,ptag+1>) /* prev */                                 DeleteNode(cur); /* */                         else                                 Find(head,key); /* Find */                 return true;         } }

画图说明：

当代码运行至B2时，当前节点被标记为“待删除”。

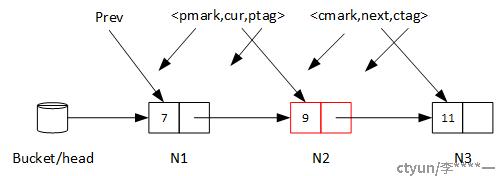
当代码运行至B3时，将prev的后继指针指向cur的后继指针，N2被删除。

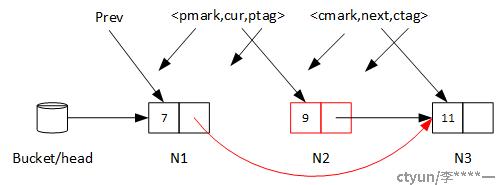
在B2时，CAS失败，意味着三个意外情况出现：

1. cur指向的元素已经被标记为删除，这个是通过判断cur的mark成员是否为1实现的
2. 在cur后面插入和新的节点（这样B3再将N1的后继指针指向N3就不对了），这个是通过判断cur的Next指针是否还指向next来实现的
3. N3已经被删除。这时cur的Next指针也不会等于next。（因为一个线程也刚刚运行到B2，此时刚刚经历过Find，cur已经被修改了）

B3失败，意味着：当前线程刚刚运行完B2时，另外一个线程将cur移除了。（那么要么prev指向的当前节点的mark不为0，要么prev的后继指针指向的不是当前节点）

查找操作

Search(head:*MarkPtrType,key:KeyType):boolean {         return Find(head,key); } Find(head:*MarkPtrType;key:KeyType) : boolean { try again:         prevhead; /* headprev*/         D1: <pmark,cur,ptag> *prev; /* prev <pmark,cur,ptag> */         while true {                 D2: if cur=null return false; /* NULL false curNULLprevhead */                 D3: <cmark,next,ctag> curˆ.<Mark,Next,Tag>;                 D4: ckeycurˆ.Key;                 D5: if *prev != <0,cur,ptag> goto try again; /* *prev */                 if !cmark {                         D6: if ckeykey return ckey=key; /* keykeyckeykey10 */                         D7: prev&curˆ.<Mark,Next,Tag>; /* curprev */                 } else {                         D8: if CAS(prev, <0,cur,ptag>,<0,next,ptag+1>) { /* */                         DeleteNode(cur); ctagptag+1;                 } else                         goto try again; /* */                 }                 D9: <pmark,cur,ptag> <cmark,next,ctag>; /* */         } }

查找操作不太好用图来说明，这里省略。

总结

综上，通过特殊的设计，实现无锁链表，那么无锁哈希表也就实现了。以上内容均参考自这篇论文：

Michael, M. M. High performance dynamic lock-free hash tables and list-based sets. In Proceedings of the fourteenth annual ACM
symposium on parallel algorithms and architectures, ACM Press, (2002), 73-82.

另外一篇论文，

Ori Shalev and Nir Shavit. Split-ordered lists: Lock-free extensible hash tables. J. ACM 53, 3 (May 2006), 379-405.

在该论文基础上进行了扩展，使得哈希表支持动态扩缩。其基本原理，还是利用了无锁单链表的既有成果：即将所有哈希表中的元素串联成为一个大的单链表。让后将哈希桶也做为这个大链表的元素，从而实现扩缩容时的元素移动（其实是移动哈希桶而不是元素）。大概是下面这个样子：

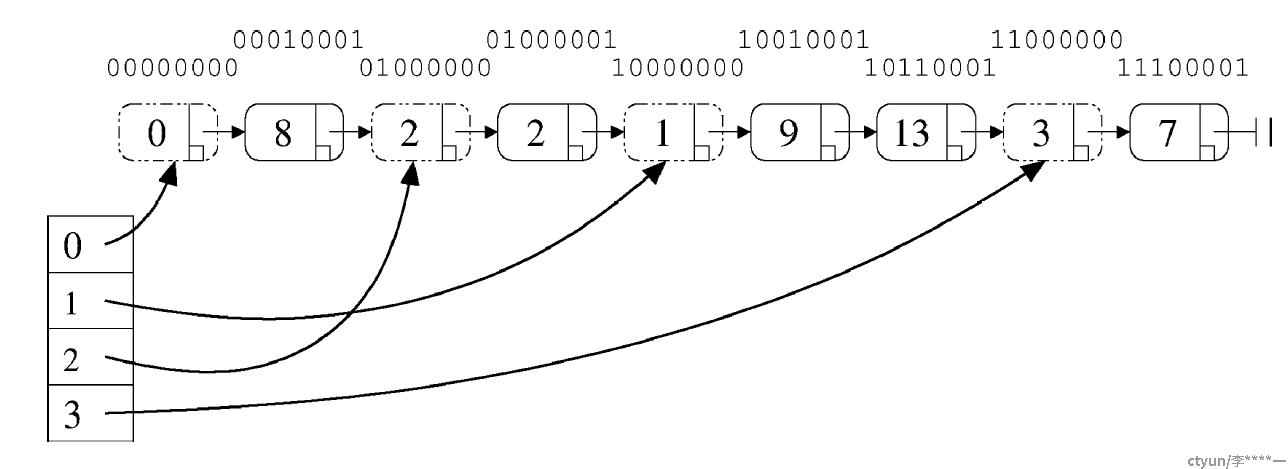
作者将其称之为“分裂排序表”。其原理由读者来验证吧。