- PageRank又称PR，佩奇排名，是由来自斯坦福大学的Larry Page与Sergey Brin在1988年提出一种根据网页之间相互的超链接计算，进行网页排名的算法。
- 通过评估链接的质量和数量来为每个页面分配相对的重要性和权威性分数，作为网页排名的要素。Larry Page将这一算法成功的应用于谷歌搜索引擎。
- PageRank算法是以随机冲浪者模型为基础在有向图中所建立一阶马尔可夫链，其描述网络一个随机冲浪者跟随网络链接随机访问网页的行为，进而通过随机冲浪者访问每个网页的概率收敛到平稳分布的极限情况时，计算出的各个网页（结点）的平稳概率值就是其所具有的PageRank值，当PageRank值越大时就说明此结点就越重要。
- PageRank算法基于网页超链接网络的链接关系，计算网页的重要程度，对网页重要性进行排序，因此提出了以下两种假设：数量假设与质量假设。
- 数量假设：在超链接网络中，如果一个网页受到来自其他网页的入链数量越多，该网页越重要。
- 质量假设：一个网页受到不同质量的网页链入时，质量更高的网页会传递更高的权重给该网页。
- 基于数量假设和质量假设，PageRank算法是通过网页上的链接进行“投票”，如果网页B存在一个指向网页A的连接，代表网页B投了网页A一次票，说明B的所有者认为A比较重要，从而给与A一部分B的重要性，网页A的“总得票”为收到所有页面重要性赋予的总和。也就是说，通过链条的所有页面的重要性确定投票的页面，有一个页面的超链接到这个网页就相当于一票。一个页面的页面排名是通过递归算法导出的，以确定其页面的所有链接（页面链接）的重要性。
- PageRank模型
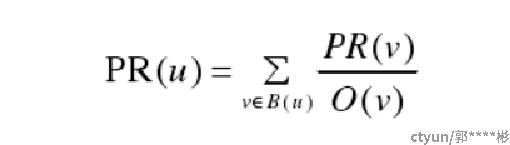
- 上述公式表示当用户正在浏览并处于某个网页时，该用户通过点击该页面中的链接继续向下浏览下个网页的概率：
- v表示一个链接到u的网页
- O（v）表示网页v的超链接数量，即出链数量
- B（u）表示所有链接到u的网页的集合。
- PageRank实例
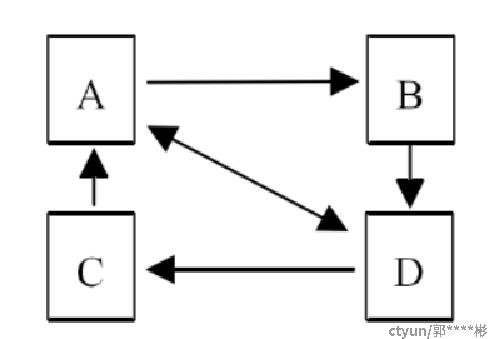
- 求解过程
- PR(A0)=PR(B0)=PR(C0)=PR(D0)=1/4
- PR(A1)=PR(C0)/L(C0)+PR(D0)/L(D0)=1/4/1+1/4/2=3/8
- PR(B1)=PR(A0)/L(A0)=1/4/2=1/8
- PR(C1)=PR(D0)/L(D0)=1/4/2=1/8
- PR(D1)=PR(A0)/L(A0)+PR(B0)/L(D0)=1/4/2+1/4/1=3/8
- 如此循环下去，直到连续两次迭代值的误差小于精度e（e>0），最终收敛。
- 用途启发
- 根据文章的链接关系或引用数据，挖掘出相较更为重要或者价值更高的知识或文章，减少检索时长及成本。
版权声明：本文内容系天翼云实名用户自发贡献，版权归原作者所有，天翼云开发者社区不拥有其著作权，亦不承担相应法律责任，未经许可，不得转载。
如有疑问或争议，请联系ctyunbbs@chinatelecom.cn删除。
0条评论
0 / 1000
