1、引子

在分布式存储的世界里，有一种冗余算法叫作擦除码(Erasure-Code), 它以多副本几分之一的成本来让存储达到同样高的可靠性。

         提高可靠性保证最简单的方法就是多副本，结合目前经验上的磁盘的损坏率(大约是年损坏率7%), 3个副本可以达到一个工业可接受的可靠性, 这个可靠性的预期大约是11个9以上(99.999999999%的概率不丢数据)。1-0.07*（0.07/365/24）^2 ～ 0.99999999999553。不过多副本显而易见的缺点就是成本比较高，为了降低成本，我们自然是希望有一种方法，在降低冗余的同时能够提高数据的可靠性。

问题1：如何实现K+1的冗余策略？

         现在我们有三个数字组成的一份数据，如何在其中再添加一个数字，使得不管这四个数字的任何一个丢失，都能够通过剩下的三个数字把缺失的那个数字恢复出来？

         思路：假设三个数字是 a、b、c。我们只需要构造一个数字 d=a+b+c，作为冗余，这样无论哪个数据丢失，都可以用剩下的三个数字计算出来。这种求和冗余的策略，就是ec算法的核心了。

问题2：如何实现K+2的冗余策略？

        让我们更进一步，假设要在数据块之中添加2份冗余块，怎么设计这两份冗余块的生成方法？

        思路1：我们把d1=a+b+c存两次，也就是d2=d1。可以实现目标吗？假设我们丢失了d1，a两份数据，那么我们可以通过a=d2-b-c，d1=d2来恢复数据。但是如果丢失了a和b两个数据，则联立d1d2，发现

a+b=d1-c

a+b=d2-c=d1-c

         这个方程组有无穷多个解，是无法恢复a和b的。所以我们在构造d2的时候，必须给abc构造不同的系数，保证在任意两个块丢失的时候，联立出来的方程都有唯一解。

        思路2：

d1=a+b+c

d2=a+2b+3c 或者 d2=a+2b+4c

        也就是说，我们只需要保证最终丢失2个数字构成的方程组有唯一解就可以。

        结论：到这里我们就得到了k+2的EC的算法: 通过166%的冗余，实现差不多和三副本300%冗余一样的可靠性，也就是说三分数据挂两份，都还能恢复回来。

问题3：如何实现K+m的冗余策略？

        通过问题2，我们发现对于增加更多冗余来说，我们新增的校验块d3也需要选择一组和d1、d2不同且任意两个式子的任意两个相同系数不能成比例。我们可以这样选择：

d1=a+b+c

d2=a+2b+4c

d3=a+3b+9c

        通过不断的增加不同的系数, 就可以得到任意的k+m的EC冗余存储策略的实现。如果要恢复数据，只需要解相应的多元一次方程组就可以，因为我们的构造方法，保证了在m个块之内的损坏，数据都可以通过剩下数据组成的方程组算出来。

       要构造一个多元一次方程组，让数据在损失若干个数据块的情况下可以获得恢复，就要求我们需要预先通过这几块数据另外计算出几个数值(校验块), 校验块和数据块构成1个整体, 每一个校验块必须具备所有数据块的特征, 可以用于和其他几个数据配合起来找回丢失的数据块。

      如果有k个数据块, 我们把k个数据作为系数, 来定义1条关于x的高次曲线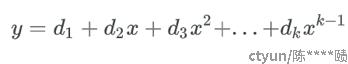：，假设我们要生成3个校验块，则有：

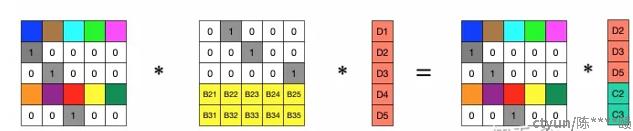
      这样，我们通过构造一条跟所有数据块作为系数的高次曲线，再曲线上去取m个点，就可以获取m个冗余校验块。这组等式又可以写成矩阵，而通过这种EC校验块的生成矩阵，构造出来的校验块，就是范德蒙矩阵。

     EC生成的过程，称之为编码，数据丢失恢复的过程，称之为解码。解码就是解n元一次方程组，比如丢2个块，就是2元一次方程组。比如这里d2、d3丢失了，随便选两个校验块参与解码就可以，不一定非得y2，y3。

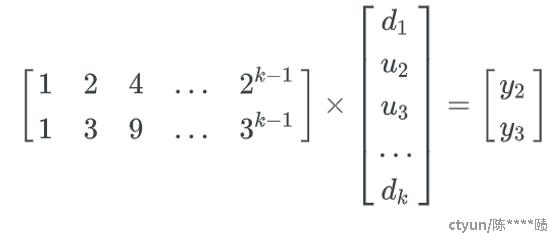
     范德蒙矩阵能够保证任意m行m列组成的子矩阵都是线性无关的，因此构成的方程肯定是有解的。

2、待解决的问题

     目前看上去，理论很完美了，但是在算法的实现中，会有个问题。就是校验块的数字大小可能会远大于数据块。在我们理想中，校验块和数据块的大小应该一致，但观察算法我们可以发现，高次方程的计算结果往往远大于作为系数的校验块。这可能会带来数据越界的问题。如果用浮点数表示法会丢失精度，导致无法恢复数据。

     所以我们在实现的时候，必须要解决数字大小的问题。

要解决数据大小越界问题，在算法框架不变的前提下，我们会改造其中的四则运算规则。这里会用到伽罗华域（有限域）的概念，具体的数学细节不展开，大致说明一下思路。有兴趣可以参考：https://www.cnblogs.com/yupence/p/16491011.html

     以RS 码为例，纠删码实现于具体的存储系统可以分为几个部分：编码、解码和修复过程中的计算都是在有限域上进行的；编码过程即是计算生成矩阵（范德蒙德或柯西矩阵）和所有数据的乘积；解码则是计算解码矩阵（生成矩阵中某些行向量组成的方阵的逆矩阵）和重建数据的乘积。

     思路：通过有限域，将计算的元和结果都限定在一个特定的范围之内，防止数据大小越界。针对计算机工程实现的特点，所有的数据都是0,1组成的，我们根据不同的字节数，可以选择GF（2⁸）、GF（2¹⁶）、GF（2³²）的有限域来实现每次对1字节、2字节、4字节的数据进行EC编解码。

     有限域是纠删码中运算的基础域，所有的编解码和重建运算都是基于某个有限域的。不止是纠删码，一般的编码方法都在有限域上进行，比如常见的AES 加密中也有有限域运算。使用有限域的一个重要原因是计算机并不能精确执行无限域的运算，比如有理数域和虚数域。

     此外，在有限域上运算另一个重要的好处是运算后的结果大小在一定范围内，这是因为有限域的封闭性决定的，这也为程序设计提供了便利。比如在RS中，我们通常使用GF(2^8)，即0～255这一有限域，这是因为其长度刚好为1字节，便于我们对数据进行存储和计算。

     在确定了有限域的大小之后，通过有限域上的生成多项式可以找到该域上的生成元，进而通过生成元的幂次遍历有限域上的元素，利用这一性质我们可以生成相应的指数表。通过指数表我们可以求出对数表，再利用指数表与对数表最终生成乘法表。

     有了乘法表，我们就可以在运算过程中直接查表获得结果，而不用进行复杂的多项式运算了。同时也不难发现，查表优化将会成为接下来工作的重点与难点。

     以GF（2⁸）为例，能够满足EC运算的几个性质:

• 加法单位元: 0
• 乘法单位元: 1
• 每个元素对加法都有逆元(可以实现减法): 逆元就是它本身( (x+1) + (x+1) = 0 )
• 每个元素对乘法都有逆元(除了0)(可以实现除法):P₈(x)是不可约的, 因此不存在a和b都不是0但ab=0; 又因为GF(2⁸)只有255个非0元素, 因此对a,总能找到1个x使得 aˣ = a . 所以 aˣ⁻² a = 1. aˣ⁻² 是a的乘法逆元.
• 乘法和加法满足分配率: 基于多项式乘法和加法的定义.

    GF(2⁸) 下的加减法直接用异或计算, 不需要其他的工作.GF(2⁸) 下的乘法和除法用查表的方式实现。

    到现在为止，我们掌握了生成矩阵的构造方法，又掌握了有限域内的四则运算法则（从而防止校验块数据溢出），我们可以开始阐述EC的编解码过程了。

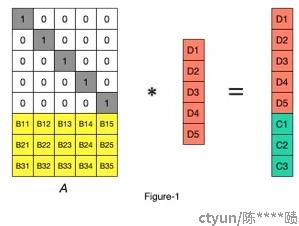
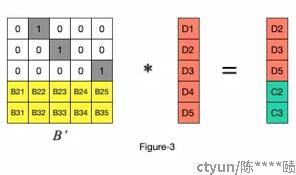
         在工程实践中，往往不会直接使用范德蒙矩阵作为ec的生成矩阵，原因是在有限域下，范德蒙矩阵的结果可能会不可逆，而不可逆的矩阵是无法还原出缺损块的，因而需要通过高斯消元后才能使用。柯西矩阵运算简单，只不过需要计算乘法逆元，我们可以提前计算好乘法逆元表以供生成编码矩阵时使用。

有限域上的求逆方法和我们学习的线性代数中求逆方法相同，常见的是高斯消元法，算法复杂度是O(n^3)。过程如下：

• 在待求逆的矩阵右边拼接一个单位矩阵
• 进行高斯消元运算
• 取得到的矩阵左边非单位矩阵的部分作为求逆的结果，如果不可逆则报错

3、各种EC算法实现

工程实现上会有很多EC算法，在不同的侧重点进行优化。

Reed-Solomon编码

经典实现：

1). ISA：ISA是Intel提供的一个EC库，只能运行在Intel CPU上，它利用了Intel处理器本地指令来加速EC的计算。

2). Jerasure是一个ErausreCode开源实现库，它实现了EC的RS编码。目前Ceph中默认的编码就是Jerasure方式

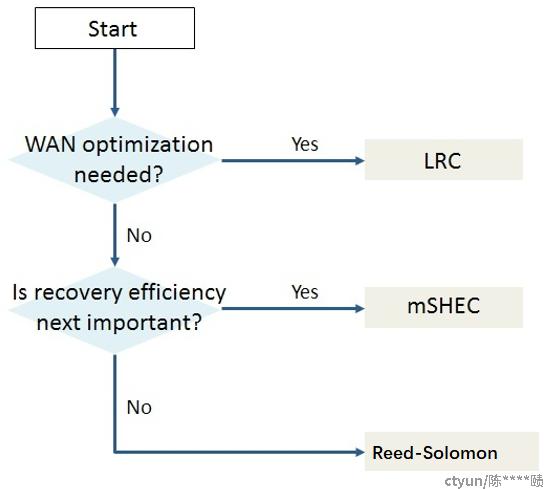
      RS编码的不足之处在于：在N+K个数据块中有任意一块数据失效，都需要读取N块数据来恢复丢失数据。在数据恢复的过程中引起的网络开销比较大。因此，LRC编码和SHEC编码分别从不同的角度做了相关优化。

LRC编码

       当 EC 进行数据恢复的时候, 需要k个块参与数据恢复, 直观上, 每个数据块损坏都需要k倍的IO消耗.为了缓解这个问题, 一种略微提高冗余度, 但可以大大降低恢复IO的算法被提出: [Local-Reconstruction-Code], 简称 LRC.LRC的思路很简单, 在原来的 EC 的基础上, 对所有的数据块分组对每组在做1次 k’ + 1 的 EC. k’ 是二次分组的每组的数据块的数量。

       LRC编码的核心思想为：将校验块（parity block）分为全局校验块（global parity）和局部校验块（local reconstruction parity），从而减少恢复数据的网络开销。

LRC（M，G，L）的三个参数分别为：

M是原始数据块的数量。

G为全局校验块的数量。

L为局部校验块的数量。

       编码过程为：把数据分成M个同等大小的数据块，通过该M个数据块计算出G份全局效验数据块。然后把M个数据块平均分成L组，每组计算出一个本地数据效验块，这样共有L个局部数据校验块。

       其实LRC的本质非常简单，它就是针对性地优化了每个子分区只有一块数据出问题的情况。对于同一分区出现两块及以上数量的坏块的情况，还是需要跟rs一样用全局修复。

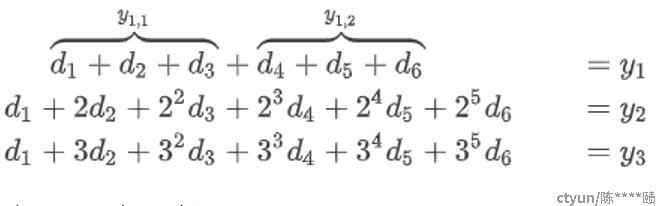
最终保存的块是所有的数据块: d₁, d₂, d₃, d₄, d₅, d₆ , 和校验块 y₁₁, y₁₂, y₂, y₃.

这里不需要保存 y₁ 因为 y₁ = y₁₁ ^ y₁₂ .

对于 LRC的EC来说, 它的生成矩阵前k行不变, 去掉了标准EC的第k+1行(全1的行), 多出2个局部的校验行:

        这样，在数据恢复的时候，如果d1，d2，d3中坏了一块d2，就可以只取d1，d3，y11 3块数据就可以恢复出d2的数据。相当于是一个纠删码的分组子集。但如果d1，d2同时坏掉，这个时候就需要进行全局恢复，从全局校验块中再取一块，进行全局恢复。其代价等同于rs。

Muti-shec编码

       SHEC编码是一种交叉分组码，方式为SHEC（K，M，L），其中K代表原始数据块data chunk的数量，M代表校验块parity chunk的数量，L代表计算校验块parity chunk时需要的原始数据块data chunk的数量。其最大允许失效的数据块为：ML/K。这样恢复失效的单个数据块只需要额外读取L个数据块。

       以SHEC（10，6，5）为例，其最大允许失效的数据块为：M(6) * L(5)/ K(10 ) = 3，且当一个数据块失效时，只读取5个数据块就可以恢复。如图所示，展示了一个参数为(10, 6, 5)的交叉分组码，交叉分组码的思想是使各个分组相互重叠，从而在多个块失效时可以利用较少的组进行局部修复。假设d3失效，我们只需要取d1,d2,d4,d5,p1或者d4,d5,d6,d7,p2，即可恢复出d3。

       图中的SHEC(10, 6, 5)是将10个数据块分为相互重叠的6个组，每组包含5个数据块，除了第3组和4组，其他任意2组之间重叠3个数据块，每组的校验块均通过组内的5个数据块运算产生，这样，单个块的失效修复只需要下载6或7个块，可见SHEC码避免了下载数据量随着失效块数增加而急剧增长的情况，但是SHEC码中所有冗余校验块均为局部校验，没有保留全局校验，这样就导致了容错能力的下降。

Clay编码

这个是18年新出现的一种编码方法，Clay 码能够将一般的MDS 码（最优容错）转化为具有最优修复的编码方法，具有以下性质：

1. Minimum Storage （最小存储开销，同经典RS码和最小存储再生码，MSR）
2. Maximum Failure Tolerance（最大容错，即 (n,k)-Clay 码可以容任意n-k 失效）
3. Optimal Repair Bandwidth （最优修复开销，能够达到理论最优值）
4. All-Node Optimal Repair （最小开销修复所有节点的数据，包括原始数据和校验数据）
5. Disk Read Optimal （最优磁盘读）
6. Low Sub-packetization （低分包数，即码字长度短）

下面以(n=4,k=2) 来介绍Clay 码，一种将一般MDS 码转化为MSR 码的方法。

Clay 是Coupled Layer 的结合，包含了Clay 码的两个特点：1 将MDS 码分层处理；2 分层之间耦合数据。

一个(4,2)-MDS 码编码后的数据有4 份，可以摆放成一个正方形。

四个(4,2)-MDS 码编码后的数据可以形成一个四层的棱柱，四棱柱的四个边对应着四个存储节点，边上的四个点所代表的数据存储于同一个节点。（下图a_0/b_0/c_o/d_0 都存在同一个节点）

耦合是将分层中不同数据进行线性组合，以实现最小修复开销。

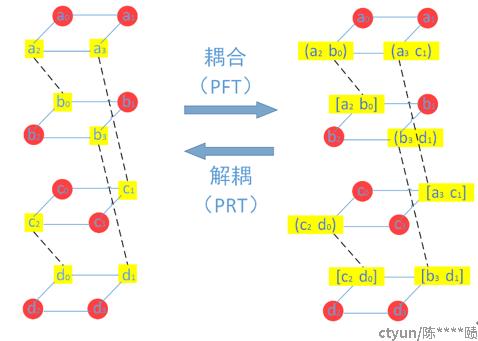
Clay 修复该节点失效只需要第二层和第三层的剩余数据块（如上图（中）所示），修复步骤如下：

1. 两个耦合的数据块(b_3,d_1) 和[b_3, d_1] 解耦得到b3 和d1，如上图（右）
2. 第二层通过b1，b3 的MDS 解码得到b_0, b_2，第四层MDS 解码得到d_0，d_2
3. 利用第二层中[a_2, b_0] 和步骤2 得到的b_0 得到a_2，同理得到c_2；

我们可以看到，(4,2) 编码最小修复开销为(n-1)α/m = 3α/2 = 6，也就是修复4块数据仅需要加载6块数据，这也是其他MSR 的最小理论修复开销。下图给出了原a_2 数据块所在节点的修复过程。

 

参考链接：

1. https://www.usenix.org/sites/default/files/conference/protected-files/fast18_slides_vajha.pdf
2. https://blog.csdn.net/sinat_22510827/article/details/110407239
3. https://www.jianshu.com/p/775f59458148

还有许许多多其他的ec编码算法，参考文献：http://html.rhhz.net/HEBGCDXXB/html/201811066.htm

四、EC性能与可靠性分析

纠删码 EC 和 副本 Replicated 的比较:

众所周知在创建Ceph的pool时，可以设置pool的冗余恢复方式，EC类型或者Replicated副本类型。指定EC类型时，可以设置N和M的参数。各种纠删码（EC的） 和 副本（Replicated）的比较如下表所示：

说明如下：

       在副本类型（三副本）的情况下，恢复效率和可靠性都比较高，缺点就是数据容量开销比较大。EC的RS编码，和三副本比较，数据开销显著降低，以恢复效率和可靠性为代价。EC的LRC编码以数据容量开销略高的代价，换取了数据恢复开销的显著降低。EC的SHEC编码用可靠性换代价，在LRC的基础上进一步降低了容量开销。

 

可靠性计算：

       2个校验块时的几个典型的可靠性比较, 第一行k=1时, 就是1+m的EC, 实际上等同多副本的策略了。

k+m EC 的数据丢失风险: