遗传算法（Genetic Algorithm, GA）起源于对生物系统所进行的计算机模拟研究。它是模仿自然界生物进化机制发展起来的随机全局搜索和优化方法，借鉴了达尔文的进化论和孟德尔的遗传学说。

由于遗传算法是模拟自然规律的一种算法，它常用术语也都是用自然科学的名词来代替，主要有以下部分：

1.个体：问题的一个解（无论可行）

2.种群：问题的一个解的集合，包含多个个体

3.染色体：个体以编码形式的存在方式

4.基因：标识染色体的信息最小存在

5.遗传：产生新个体的方式

6.适应度：个体对应问题的解决能力

遗传算法简单来说分为以下几个阶段：编码、生成初始种群、遗传操作、筛选。

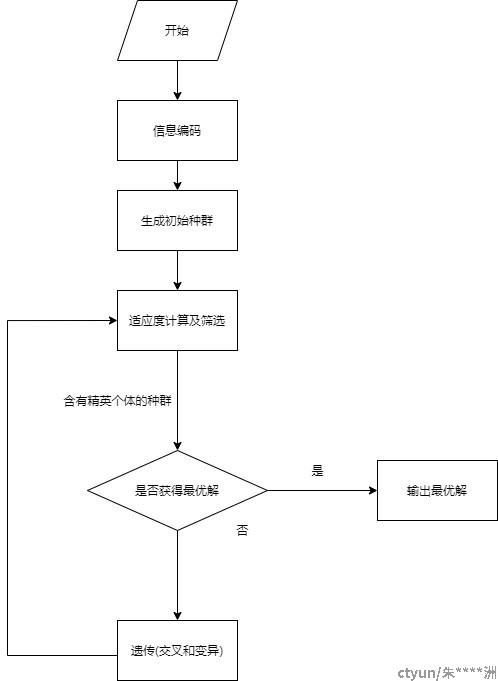
图2.1为遗传算法运用的流程图，其分为以下步骤：

1.编码

编码是体现遗传算法借鉴生物学遗传学说的重要环节，具体表现为将信息以特殊编码的形式保存，称之为染色体，是后续遗传操作的最小单位。优秀的编码方式能够将个体的信息详尽保存，提升算法的效率。

常见的编码方式有二进制编码、格雷编码、浮点数编码、符号编码等

2.初始种群生成

初始种群是在遗传算法刚开始的时候随机生成的多个初始解。初始种群不能确定遗传算法的优劣，但优秀的初始种群的设计可以保证遗传算法的迭代次数较少，种群多样性大，能够更快地达到最终的最优解。

初始种群是随机生产的个体的集合，根据遗传算法的使用方式，初始种群生成的方式也不同。

3.遗传操作

遗传操作主要分为交叉和变异两种，其主要目的是为了产生新的个体，提高种群中个体的多样性。在一次次的遗传过程中，总会留下优秀的个体，才能产生最终理想的结果。

交叉是将两个个体的染色体中的基因进行互换，或者直接将部分染色体进行互换，从而得到新的个体。交叉是主要的遗传手段。

变异是将一个个体中的基因进行随机变化，从而获得新的染色体，因而新的个体诞生。在种群中，变异的概率一般设置得并不高。

4.筛选

在每次的遗传后，对于新种群要去进行适应度的评估以及淘汰。适应度函数的选取直接影响到遗传算法的收敛速度以及能否找到最优解。适应度函数设计有很多种，可以通过罚函数对冲突进行惩罚。

常见的筛选方法有轮盘赌选择法、随机便利抽样法、锦标赛选择法

总结：

遗传算法普遍用于数值优化、组合优化、机器学习等问题领域，由于其不需要借助额外的梯度信息或辅助知识，只需要搜索方向的目标函数和适应度函数，因而提供了一种解决问题的通用框架。