1. 简介

       HNSW将空间中的向量按下图的形式组织，每一个节点插入时，首先将数据保存在第0层。然后随机一个层数，从该层开始逐层往下遍历，每层都将该节点(以节点内部id代表)插入，并按一定规则(后文介绍)连接M个近邻节点，直至第0层。

2. 详细过程

2.1 NSW(Navigable Small World graphs)

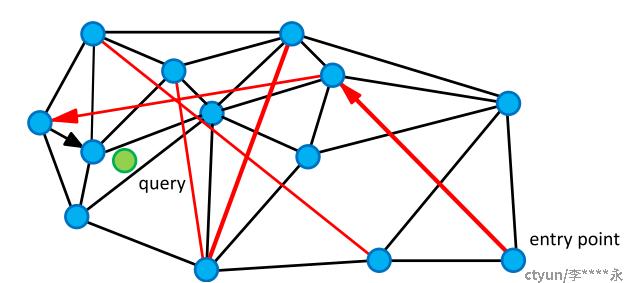
“高速公路”机制（Expressway mechanism, 指部分远点之间拥有线段连接，以便于快速查找）。

       NSW论文中配了这样一张图，黑色是近邻点的连线，红色线就是“高速公路机制”了。我们从enter point点进入查找，查找绿色点临近节点的时候，就可以用过红色连线“高速公路机制”快速查找到结果。

       NSW朴素构图算法在这里：向图中逐个插入点，插图一个全新点时，通过朴素想法中的朴素查找法（通过计算“友点”和待插入点的距离来判断下一个进入点是哪个点）查找到与这个全新点最近的m个点（m由用户设置），连接全新点到m个点的连线。

       首先，我们的构图算法是逐点随机插入的，这就意味着在图构建的早期，很有可能构建出“高速公路”。假设我们现在要构成10000个点组成的图，设置m=4（每个点至少有4个“友点”），这10000个点中有两个点，p和q，他们俩坐标完全一样。假设在插入过程中我们分别在第10次插入p，在第9999次插入q，请问p和q谁更容易具有“高速公路”？答：因为在第10次插入时，只见过前9个点，故只能在前9个点中选出距离最近的4个点（m=4）作为“友点”，而q的选择就多了，前9998个点都能选，所以q的“友点”更接近q，p的早期“友点”不一定接近点p，所以p更容易具有“高速公路”。结论：一个点，越早插入就越容易形成与之相关的“高速公路”连接，越晚插入就越难形成与之相关的“高速公路”连接。所以这个算法设计的妙处就在于扔掉德劳内三角构图法，改用“无脑添加”（NSW朴素插入算法），降低了构图算法时间复杂度的同时还带来了数量有限的“高速公路”，加速了查找。

2.2 NSW算法优化

        一. 在查找的过程中，为了提高效率，我们可以建立一个废弃列表，在一次查找任务中遍历过的点不再遍历。在一次查找中，已经计算过这个点的所有友点距离查找点的距离，并且已经知道正确的跳转方向了，这些结果是唯一的，没有必要再去做走这个路径，因为这个路径会带给我们同样的重复结果，没有意义。

        二. 在查找过程中，为了提高准确度，我们可以建立一个动态列表，把距离查找点最近的n个点存储在表中，并行地对这n个点进行同时计算“友点”和待查找点的距离，在这些“友点”中选择n个点与动态列中的n个点进行并集操作，在并集中选出n个最近的友点，更新动态列表。注意，插入过程之前会先进行查找，所以优化查找过程就是在优化插入过程。以下给出NSW查找步骤。设待查找q点的m个近邻点。

 1.随机选一个点作为初始进入点，建立空废弃表g和动态列表c，g是变长的列表，c是定长为s的列表（s>m）,将初始点放入动态列表c（附上初始点和待查找q的距离信息），制作动态列表的影子列表c'

 2.对动态列表c中的所有点并行找出其“友点”，查看这些“友点”是否存储在废弃表g中，如果存在，则丢弃，如不存在，将这些 剩余“友点”记录在废弃列表g中（以免后续重复查找，走冤枉路）

 3.并行计算这些剩余“友点”距离待查找点q的距离，将这些点及其各自的距离信息放入c

 4.对动态列表c去重，然后按距离排序（升序），储存前s个点及其距离信息

 5.查看动态列表c和c'是否一样，如果一样，结束本次查找，返回动态列表中前m个结果。如果不一样，将c'的内容更新为c的 内容，执行第2步

        三. 插入算法更简单了，插入算法就是先用查找算法查找到m个（用户设置）与待插入点最近的点，连接它们。

2.3 跳表

       设有有序链表，名叫sorted_link，里面有n个节点，每个节点是一个整数。我们从表头开始查找，查找第t（0<t<n）个节点 需要跳转几次？答：t-1次（没错，我是从1开始数的）。把n个节点分成n次查找的需求，都查找一遍，需要跳转几次？答： （0+1+2+3+.....+（n-1））次。

       如果我这链表长成下图这样呢？

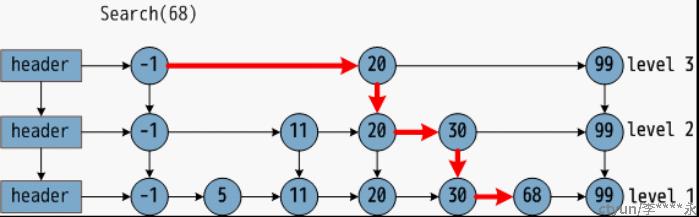
       这已经不是一个有序链表了，这是三个有序链表+分层连接指针构成的跳表了。看这张示意图就能明白它的查找过程，先查第一层，然后查第二层，然后查第三层，然后找到结果。如果把上段所描述的名字叫sorted_link的链表建立成这样的跳表，那么把sorted_link中的所有元素都查一遍还需要花费（0+1+2+3+.....+（n-1））次吗？当然不需要。那么具体是多少次呢？如果你真的关心，请搜狗搜索关键词“跳表”。

       跳表怎么构建呢？三个字，抛硬币。对于sorted_link链表中的每个节点进行抛硬币，如抛正，则该节点进入上一层有序链 表，每个sorted_link中的节点有50%的概率进入上一层有序链表。将上一层有序链表中和sorted_link链表中相同的元素做一一对应的指针链接。再从sorted_link上一层链表中再抛硬币，sorted_link上一层链表中的节点有50%的可能进入最表层，相当于sorted_link中的每个节点有25%的概率进入最表层。以此类推。

       这样就保证了表层是“高速通道”，底层是精细查找，这个思想被应用到了NSW算法中，变成了其升级版-----HNSW。

2.4 HNSW(Hierarchical Navigable Small World graphs)

2.4.1 添加节点

       添加节点时，先检查一下该节点的label是否已经存在了，如果存在的话，直接更新节点，下一节会详细介绍。如果不存在，则直接添加节点。主要步骤为：

1. 1. 节点id自增加1
   2. 随机初始化层数 curlevel
   3. 初始化节点相关数据结构，主要包括：将节点数据以及label拷贝到第0层数据结构(data_level0_memory_)中；为该节点分配存储0层以上的邻居关系的结构，并将其address存储在linkLists_中
   4. 如果这是第一个元素，只需将该节点作为HNSW的entrypoint，并将该元素的层数作为当前的最大层。
   5. 如果不是第一个元素：1）那么从当前图的从最高层逐层往下寻找直至节点的层数+1停止，寻找到离data_point最近的节点，作为下面一层寻找的起始点。2）从curlevel依次开始往下，每一层寻找离data_point最接近的ef_construction_（构建HNSW是可指定）个节点构成候选集，再从候选集中选择M个节点与data_point相互连接。至于如何寻找ef_construction_个候选节点，在后文搜索节点一节中解释。

       这里值得注意的一点是 ：若候选集(top_candidates)中节点的数量大于M时，如何从中选择M个节点与data_point相连。首先容易想到的是从候选集中选择最近的M个点。这样有一个问题，就是容易形成孤岛。如下图所示，a点为将要插入的点。假设M为2，如果找寻最近的2个黑色的点与之相连，则黑色的点肯定在cluster1中，这样就造成cluster1与cluster2分裂，最终构成的图也不是连通图，会影响搜索结果。

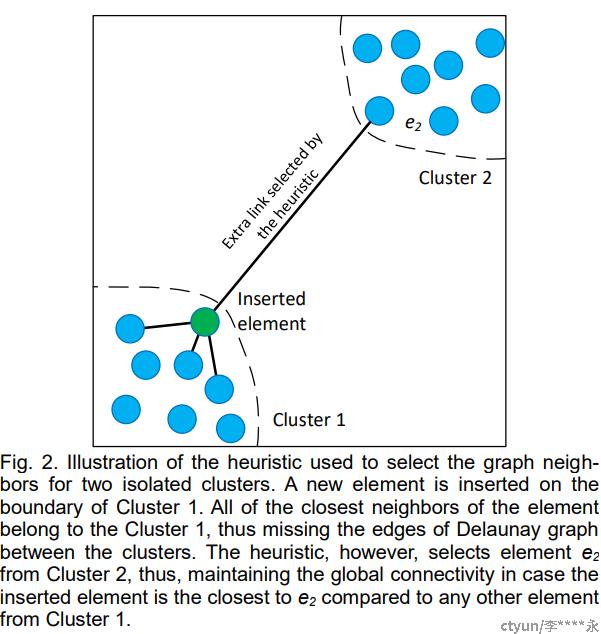
       为了防止cluster分裂，hnswlib采用一种叫启发式搜索的方法。每选择一个节点时，都要看此节点到目标节点a的距离是否比此节点到所有已选中的节点远，如果远，则选中它。上图中先选c0，计算c1时，因为它距离c0比距离a近，所以可能c0和c1属于一个集群，故不选它，而选择c2。 现假设c0~c3都在候选集中，从中选择两个节点相连。详细步骤如下：

1. 1. 先将c0~c3按照到a点的距离从近到远排序，为c0, c1,c2,c3，放在队列queue中。
   2. 从队列中依次取出一个节点，第一次取c0,将c0选为a的邻居，先存在return_list中。
   3. 再从队列中取出下一个节点c1，计算出c1到a点的距离d1。依次计算return_list中已选中的所有节点(也就是c0)到a点的距离，并与d1相比较，发现c0和c1更近，因此不选c1
   4. 在从队列中取出一个节点c2，计算出c2到a点的距离d2。依次计算return_list中已选中的所有节点(也就是c0)到a点的距离，并与d2相比较，发现c0和c2更远，选中c2
   5. 至此，return_list的size为2，结束筛选。

2.4.2 更新节点

     插入节点时，如果节点的label已经存在了，那么直接更新节点。更新节点主要分为三步：

1. 1. 更新节点的数据；直接把数据拷贝到0层相应的位置即可。
   2. 从0层逐层往上，直至该节点的最高层，在每一层取待更新节点的部分邻居，更新它们的邻居；for循环遍历每一层，在for循环里面，首先挑部分原来的邻居，存储在 sNeigh里面， 比例由参数updateNeighborProbability控制。而将待更新节点经过一跳，二跳到达的节点存在sCand里面，供后面更新邻居的时候选择。然后，对sNeigh中每一个选中的待更新的邻居n，利用启发式搜索(getNeighborsByHeuristic2)在sCand中选出最多M个点，将它们作为n的邻居存储在n的数据结构对应的位置。
   3. 从上往下依次更新待更新节点的邻居。更新待更新节点data_point的邻居。这个与添加节点类似：从当前图的从最高层逐层往下寻找直至节点的层数+1停止，寻找到离data_point最近的节点，作为下面一层寻找的起始点。2）从data_point的最高层依次开始往下，每一层寻找离data_point最接近的ef_construction_（构建HNSW是可指定）个节点构成候选集，再从候选集中利用启发式搜索选择M个节点与data_point相互连接。

2.4.3 搜索节点

       当我们构建好HNSW之后，就可以查询了，也就是给定一个向量(目标)，搜索最近的k个向量。也就是寻找图中，离目标点最近的k个点。HNSW利用分层的特性，先从最高层的入口点(enterpoint)开始，每一层寻找离目标点最近的点，作为下一层的入口，知道第0层。那么第0层的入口已经离目标向量很近了，所以后面的搜索就快多了。这里分两步来介绍：

1. 1. 第0层以上：0层以上比较简单，从enterpoint开始，遍历它的邻居，从邻居(包括自己)中找到离目标最近的点a。如果点a不是enterpoint，则下一次从点a开始以同样的模式搜索。如果点a和enterpoint是同一个点，也就是说，它的邻居包括自己所有点中，自己是离目标最近的点，则该层搜索结束。
   2. 第0层：维护一个长度不大于ef_construction的动态list，记为W。每次从动态list中取最近的点，遍历它的邻居节点，如果它的邻居没有被遍历过，那么当结果集小于ef_construction，或者该节点比结果集中最远的点离目标近时，则把它添加到W中，如果该点没有被标记为删除，则添加到结果集。如果添加后结果集数量多于ef_construction，则把最远的pop出来。此种思想有点类似于BFS，只不过不同的是，这里的动态list是一个优先级队列，每次pop的是离目标最近的点。另外，结果集的数量有一个上限，需要不断的更新里面的点。

3 应用场景

     特征向量搜索

4 参考资料

1. https://arxiv.org/ftp/arxiv/papers/1603/1603.09320.pdf
2. https://www.researchgate.net/profile/Yu-Malkov/publication/259126397_Approximate_nearest_neighbor_algorithm_based_on_navigable_small_world_graphs/links/63733c302f4bca7fd06030b8/Approximate-nearest-neighbor-algorithm-based-on-navigable-small-world-graphs.pdf
3. https://arxiv.org/ftp/arxiv/papers/1603/1603.09320.pdf
4. https://github.com/erikbern/ann-benchmarks