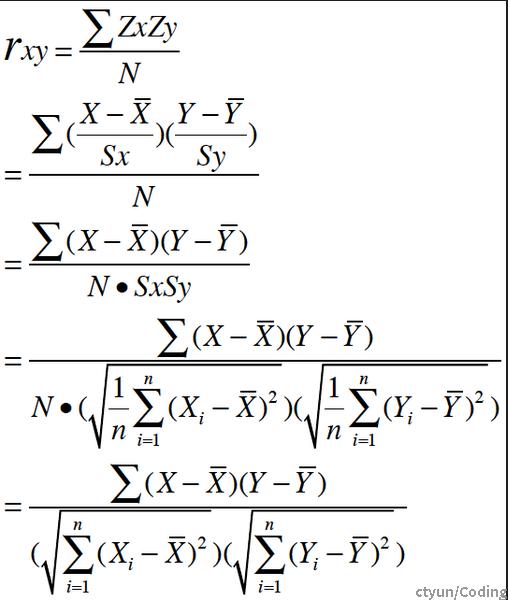相似度是指两个对象之间的相似程度和相关程度,在机器学习中有广泛的使用。通过计算不同数据点之间的相似度,可以将它们分组为具有相似特征和行为的集群。这对于数据分析和聚类任务非常重要,可以被应用在推荐系统、图像和语音识别、异常检测和异常值排除、搜索引擎等等场景中。
在计算相似度时,常用的有欧几里得距离、曼哈顿距离、余弦相似度、皮尔逊系数等,在此对这几种方法进行介绍。
一 欧氏距离
欧氏距离(Euclidean distance)是指两点之间的真实距离,也可以看作是欧几里得空间中两点之间的距离。
例如空间中有两点(x1, y1, z1)和(x2, y2, z2),他们之间的距离d计算公式如下:
d = sqrt((x2-x1)^2 + (y2-y1)^2 + (z2-z1)^2)
欧氏距离具有以下性质:
1. 非负性:两点之间的距离总是非负的,即d≥0。
2 齐次性:两点之间的距离与坐标系的缩放无关,即如果将坐标系缩放k倍,则两点之间的距离也缩放k倍。
3 三角形不等式:对于任意三点A、B、C,有d(A,B)+d(B,C)≥d(A,C)。
欧氏距离有计算简单、适用性强的优点,在数据分析中被广泛的使用,也可以用于生物信息学,对基因和蛋白质进行聚类分析。但是它也存在一些缺点,例如对数据分布敏感,如果样本数据分布不均匀,很可能导致聚类结果不准确。
二 曼哈顿距离
曼哈顿距离(Manhattan Distance)也称为城市街区距离(City Block Distance),是指两个点在水平或垂直方向上的距离之和,也就是在欧几里得空间的固定直角坐标系上两点所形成的线段对轴产生的投影的距离总和。
曼哈顿距离的计算公式为:
d = |x2-x1| + |y2-y1|
其中,d表示两个点之间的曼哈顿距离,(x1, y1)和(x2, y2)是两个点在直角坐标系中的坐标。
曼哈顿距离是一种常见的距离计算方法,与欧氏距离相同具有非负性、齐次性、三角形不等式。它适用于处理高维数据,对离群点不太敏感,在地理信息系统(GIS)中应用很广泛。欧氏距离和曼哈顿距离都有对离群点敏感的缺点,但它们的敏感程度不同。欧氏距离在计算两个向量之间的距离时,容易受到单个维度的离群值的影响,而曼哈顿距离则对每个维度上的离群值都不敏感,因为它只计算绝对值的和。
三 余弦相似度
余弦相似度(Cosine Similarity)是一种用于衡量两个向量之间相似度的度量方法。它的计算基于向量的夹角余弦值,即两个向量在空间中的相对位置。余弦相似度广泛应用于文本处理、信息检索、机器学习等领域。
余弦相似度的计算公式如下:
cosine_similarity = (A · B) / (||A|| ||B||)
其中,A和B是两个向量,"·"表示向量的点积运算,"|| ||"表示向量的模(范数)。
余弦相似度的值在-1和1之间。当两个向量的方向完全相同时,余弦相似度为1,表示它们相似度很高;当两个向量的方向完全相反时,余弦相似度为-1,表示它们相似度很低;当两个向量之间的夹角为直角(正交)时,余弦相似度为0,表示它们无相似关系。
余弦相似度的优点是对向量的长度不敏感,只考虑向量的方向。这使得它在处理文本分类、推荐系统、聚类分析等任务中非常有用。在这些任务中,向量表示的维度通常很高,但与目标相关的特征较少,因此使用余弦相似度可以消除向量长度对相似度计算的影响。但是它的缺点也是不考虑绝对值的大小,在处理稀疏数据时表现不佳。
四 皮尔逊系数
皮尔逊系数(Pearson correlation coefficient)是一种用于测量两个变量之间线性相关性的统计指标。它衡量了两个变量之间的线性关系程度,取值范围在-1到1之间。皮尔逊系数为正表示两个变量之间存在正相关关系,为负表示存在负相关关系,而为0表示两个变量之间没有线性关系。
| 相关系数 | 相关强度 |
| 0.8-1.0 | 极强相关 |
| 0.6-0.8 | 强相关 |
| 0.4-0.6 | 中等程度相关 |
| 0.2-0.4 | 弱相关 |
| 0.0-0.2 | 极弱相关或无相关 |